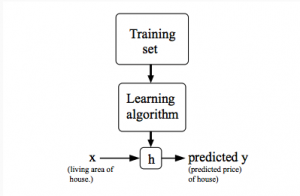
개요
[math]\displaystyle{ h(x) = a_{0} + a_{1} * x_{1} + a_{2} * x{2} + a_{3} * x{3} .... }[/math] 처럼 선형의 다항식으로 표현되는 회귀 분석 모델을 구하는 과정이다.
이 식은 벡터 형식으로 표현하면 다음과 같이 표현할 수 있다.
- [math]\displaystyle{ \begin{align*}h_\theta(x) =\begin{bmatrix}\theta_0 \hspace{2em} \theta_1 \hspace{2em} ... \hspace{2em} \theta_n\end{bmatrix}\begin{bmatrix}x_0 \newline x_1 \newline \vdots \newline x_n\end{bmatrix}= \theta^T x\end{align*} }[/math]
- [math]\displaystyle{ x_{0}^{(i)} =1 \text{ for } (i\in { 1,\dots, m } ) }[/math]
- x는 입력값
- 세타는 가중치
모델 설명
[math]\displaystyle{ (x^{i}, y^{i}) }[/math] 로 표현되는 순서쌍이 주어진다고 하자. 이때 구하고자 하는 것은 [math]\displaystyle{ (x^{k}, y^{k}) }[/math] 가 주어진 경우 주어졌던 순서쌍에 의거한 예측값을 도출하는 함수를 만드는 것이다.
선형 결합의 형태로 표현된 함수를 이용하여 추정치를 추측하는 함수를 만든다. 쉽게 설명하자면, N차원의 입력값이 주어지는 경우 N개의 변수를 받을 수 있는 함수를 만들면 된다. 이를 선형적으로 만드면 위에서 설명한 h가 나온다. 물론 비선형적으로도 만들 수 있지만, 지금 우리가 하고자 하는 것은 이를 선형적으로 만드는 것이 목표 이기 때문에, 이렇게 한다. 선형적이라 하는 것은 최고차항의 계수가 1임을 말한다. (엄밀하게 선형적이라 함은 H(a+b) = H(a) + H(b) 이고 H(ax) = aH(x)이지만, 다항함수에서는 이런 함수는 1차 함수가 최대임으로) 따라서 우리는 이 선형함수의 계수를 추정하는 방법을 통해 선형 함수를 추론하게 된다.
주의 할점
- 선형적이라 함은 결과적으로 추론하는 함수 h가 선형적이라는 것이지, 반드시 그래프에 직선으로 예측한다는 걸 의미하는 것은 아니다. 왜냐하면 입력 값을 변형시켜 마치 다항함수나 다른 함수로 추론하는 것처럼 만들 수도 있기 때문이다.
- 선형회귀 모델은 Overfitting에 취약하다.
선형 회귀 모델 추정 기법
오차 함수
선형 회귀 모델을 수렴시키기 위해서 오차 함수를 정의하여 그 오차 함수가 최소가 되는 방향으로 함수에 압력을 넣는다. 이하는 선형 회귀에서 사용하는 여러 오차 함수와 그 오차 함수로 어떻게 선형 회귀식에 압력을 넣는지 즉, 가중치 값들을 업데이트하는 방법을 설명한다.
최소 제곱법 (MSE)
- [math]\displaystyle{ \operatorname{MSE}=\frac{1}{n}\sum_{i=1}^n(Y_i-\hat{Y_i})^2. }[/math]
로 정의되는 MSE를 이용하여 잔차를 구해 최소화 시키는 방식이다.
Minimize Log Likelihood function
가우시안 노이즈가 주어질경우, MLE방식을 통해서 잔차를 구하는 방식인데, 결국 MSE와 같은 결과가 나오게 된다.
정의
- 관측된 m개의 데이터 [math]\displaystyle{ (x, y) }[/math]에 대하여 단순 선형 회귀 모델을 다음과 같이 정의할 때,
- [math]\displaystyle{ h_\beta=\beta_0+\beta_1x }[/math]
- 손실 함수 [math]\displaystyle{ J(\beta_0, \beta_1) }[/math] 는 아래와 같이 정의할 수 있다.
- [math]\displaystyle{ J(\beta_0, \beta_1) = \frac{1}{2m}\sum_{i = 1}^{m} (h_\beta(x^{i}) -y^{i})^{2} }[/math]
이를 행렬식으로 표현하면 다음과 같다. (t는 ground truth, H basis, w weight)
- [math]\displaystyle{ w^* = arg\ min_w \sum_w (Hw-t)^T (Hw - t) }[/math]
설명
- 제곱을 하는 이유는 음수와 양수의 차이를 무시하기 위해서이다. 절대값을 사용해도 괜찮지만 미분가능성과 오차가 커질수록 반영되는 정도를 크게 하기 위해서 제곱을 하였다. 또한 이 제곱한 오차들을 모든 데이터에대해서 평균을 내야 함으로 데해서 2m으로 나눈다. m으로 나누어도 괜찮지만 2로 다시한번 나누면 나중에 처리할 미분에서 계산이 간단하게 되는 이점이 있다.
- 최소 제곱법으로 도출된 비용함수는 오차를 변수로 가지는 2차 함수가 된다. 이 2차 함수는 오차가 0인지점, 즉 h의 기울기가 우리가 원하는 기울가 되어서 오차가 0이 될때가 해이다. 즉 이 2차함수의 해가 우리가 원하는 기울기 즉 [math]\displaystyle{ \beta }[/math]값들이 된다. 따라서 h를 미분하여 뉴턴법과 같은 방식으로 도함수를 따라 간다면, 우리가 구하고자 하는 기울기를 알 수 있다. (뉴턴법이란 도함수의 기울기를 따라가서 해를 구하는 방식이다. 선형 회귀도 이와 비슷한 방식으로 작동한다.)
- 앞으로 정리할 모든 오차 함수가 최소 제곱법의 논리와 비슷한 방식으로 작동하기에 더 추가해 보자면, 주어진 식에서 베타의 차원이 올라가도 위에서 설명한 것과 같은 논리가 적용된다. 마치 그릇에 공이 빠지는 것처럼, 블랙홀에 행성이 빨리는 것처럼 오차 함수의 그라디언트(略:확장된 차원의 미분)은 오차의 최소점을 향하게 된다. 이를 이용해서 오차함수를 최소가 되게하는 기울기 다시말해 가중치의 벡터를 구하게 된다.
가중치 업데이트 방식
이후 다음과 같은 방식을 통해서 가중지 [math]\displaystyle{ \theta }[/math] 를 업데이트 하면 우리가 구하고자 하는 선형 함수를 구할 수 있다. 즉 학습을 시킬 수 있다.
- [math]\displaystyle{ \begin{align*}& \text{repeat until convergence:} \; \newline \; & \theta_j := \theta_j - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \; & \text{for j := 0...n}\newline \end{align*} }[/math]
여기서 우변의 식은 경사 하강법을 이용하기 위해서 그라디언트를 취한 형태이다. (미분을 취한 형태이다.)
또한 여기서 Learning Rate (윗식의 알파)가 무엇을 의미하는지 알 수 있는데, 이는 그라디언트에 곱해져 기울기 하강법의 수렴정도를 정하는 값이 된다.
Normal Equation
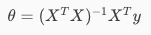
그렇다면 [math]\displaystyle{ \theta }[/math] 를 한번에 구할 수 있는 방법은 없을까? 이 방식은 Learning Rate를 구할 필요도 없고 정확한 [math]\displaystyle{ /theta }[/math]를 한번에 구할 수 있다. 이는 선형적으로 표현된 식을 이용하여 한번에 구하게 된다. 그러나 이는 역행렬을 구하는데 드는 비용이 매우큰 것과 많은 인공지능 알고리즘에서는 이렇게 단순한 알고리즘을 사용할 수 없다는 단점이 있다. 만약 n이 10,000이하의 dataset이라면 Normal Equation은 Gradient Descent보다 빠른 결과를 나타내줄 수 있으므로 사용하는 것이 이득이다.
단점
- [math]\displaystyle{ N^3 }[/math]의 시간 복잡도를 같는다.
- 만약 m이 n보다 큰경우 (데이터의 feature_분류 기준 보다 적은 dataset_사건)일 경우 역행렬을 구할 수 없다.
- 중복된 데이터 분류 기준이 존재한다. 즉 데이터 분류 기준중 선형적으로 연관된 분류 기준이 있을 경우 역행렬을 구할 수 없다.
가중치 업데이트 방식
그냥 구해진 가중치를 식에 대입한다.
Learning Rate
학습 속도는 선형 회귀가 정답에 수렴하는 정도를 정한다.
Learning Rate가 크면 정답에 빠르게 수렴하지만, 결과가 발산하거나 오르락 내리락(Ocillate)하는 문제가 생길 수도 있다. 따라서 Learning Rate에 의해서 함수가 잘 수렴하는지 검사하는 과정이 필요하다.
주로 작은 값에서 시작하여 조금씩 값을 크게해서 어떤 Learning Rate에서 선형 회귀가 최적화 되어 작동하는지 알아보는 과정을 거친다.
입력 데이터의 조정
그라디언트가 수렴하는 정도를 빠르게 하거나, 변수 값이 결과에 영향을 미치는 정도를 조절하기 위해서 들어가는 Input데이터를 수정하기도 한다.
새로운 변수세트 만들기
예를들어 집의 높이와 면적이 주어진경우 새로운 변수 "크기"를 결정하여 입력 데이터에 넣어도 됀다. 이처럼 머신 러닝에 입력되는 데이터를 주어진 데이터만 사용하기 보다는 새로 재정의해서 입력해도 된다.
Feature Scalling
입력값 평활(平闊)은 주어진 데이터의 범위가 서로 안 맞는 경우 범위를 맞추어 주는 것을 말한다.
주로 맞추어 주는 범위는 대략 [math]\displaystyle{ -1 \le x_{i} \le 1 }[/math]가 되도록 한다.
예를 들어 입력값 순서쌍이 (가격,방의 개수) 라고 해보자. 이경우에는 가격은 억단위를 넘어가지만 방의 개수는 고작해야 한자리 이기 때문에, 가격이 방의 개수 변수를 눌러버린다. 이런 경우를 해결하기 위해 적당히 입력값을 조정하여 서로의 단위를 맞추어 준다.
Mean nomalization
평균화는 주어진 데이터의 평균값이 대략 0이 되도록 입력값을 조정해 주는 것이다.
- 주로 다음과 같은 공식을 사용한다. [math]\displaystyle{ x_{i} = \frac{x_{i}-u{i}}{s_{i}} }[/math]
- s는 분산, u는 평균
Polynomial Regression
단순한 선형 함수가 아닌 다항함수로 예측을 하고 싶은 경우가 있을 수도 있다. 이 경우 다항함수는 선형함수가 아니기 때문에 선형 회귀로 나타낼 수 없는 것 처럼 보인다. 그러나 입력 데이터에 적절한 처리를 한다면 만들 수 있는 경우가 대부분이다.
- [math]\displaystyle{ \theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_1^2 + \theta_3 x_1^3 }[/math]
- 윗 식은 3차함수가 데이터를 분류하도록 한다.
- [math]\displaystyle{ \theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 \sqrt{x_1} }[/math]
이처럼 입력 데이터를 변환하여 다항 함수로 선형 회귀를 사용하고자 하면 데이터의 분산이 과장되기 때문에 Feature Scalling이 매우 중요해 진다.
Regularized Linear regression
모델이 overfit되는 것을 막기위해서
- [math]\displaystyle{ w = \text{arg}\min_w \left( \sum_{i=1}^N e_i^2 + \lambda \sum_{j=1}^M w_j^q \right) }[/math]
처럼 weight에 제약조건을 두는 것을 말한다.
(L0 norm이란 norm이 아니지만, norm처럼 표현되어 있다.)
같이 보기