개요
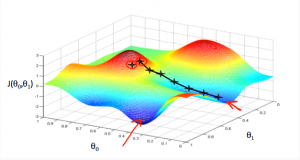
기울기 하강(Gradient Descent)은 함수의 기울기를 구해서 기울기가 낮은 쪽으로 계속 이동시켜서 극값에 이를 때까지 반복시키는 알고리즘이다.
설명
최적화할 함수 [math]\displaystyle{ f(\mathbf{x}) }[/math]에 대하여, 먼저 시작점 [math]\displaystyle{ \mathbf{x}_0 }[/math]를 정한다. 현재 [math]\displaystyle{ \mathbf{x}_i }[/math]가 주어졌을 때, 그 다음으로 이동할 점인 [math]\displaystyle{ \mathbf{x}_{i+1} }[/math]은 다음과 같이 계산된다.
- [math]\displaystyle{ \mathbf{x}_{i+1} = \mathbf{x}_i - \gamma_i \nabla f(\mathbf{x}_i) }[/math]
이때 [math]\displaystyle{ \gamma_i }[/math]는 이동할 거리를 조절하는 매개변수이다. (역 삼각형 기호는 그라디언트를 의미한다.)
- 이 알고리즘의 수렴 여부는 함수의 성질과 [math]\displaystyle{ \gamma_i }[/math]의 선택에 따라 달라진다. 또한, 이 알고리즘은 가장 가까운 최적해로 수렴한다. 따라서 구한 값이 주어진 함수의 진짜 최적해라는 것을 보장하지 않으며 시작점 [math]\displaystyle{ \mathbf{x}_0 }[/math]의 선택에 따라서 달라진다. 이에 따라 다양한 시작점에 대해 하강법을 적용하여 그 중 가장 좋은 결과를 선택할 수도 있다.
- 재귀 함수나 루프를 이용하여 최적해를 찾아 나가게 된다. 이경우 [math]\displaystyle{ \mathbf{x} = \mathbf{x} - \gamma_i \nabla f(\mathbf{x}) }[/math] 로 표현된다.
인공 지능
인공지능에서 사용하는 비용 함수도 기울기 하강의 논리를 사용하여 작동한다.
- [math]\displaystyle{ h(x) = a_{0} + a_{1} * x_{1} + a_{2} * x{2} + a_{3} * x{3} .... }[/math] 라 주어진 선형 회귀식이 있다고 해보자. 이떄 오차함수 h에 대하여 기울기 하강법을 이용해 [math]\displaystyle{ a_{0}, a_{1}, a_{2} .. }[/math]을 업데이트 하는 식을 나타내면,
- [math]\displaystyle{ \mathbf{x} = \mathbf{x} - \gamma \nabla f(\mathbf{x}) }[/math] 로 나타내 진다. 결국 기울기 하강법을 이용하면, 우리가 원하는 가중치들의 집합을 구할 수 있다.
