개요
최적화할 함수 [math]f(\mathbf{x})[/math]에 대하여, 먼저 시작점 [math]\mathbf{x}_0[/math]를 정한다. 현재 [math]\mathbf{x}_i[/math]가 주어졌을 때, 그 다음으로 이동할 점인 [math]\mathbf{x}_{i+1}[/math]은 다음과 같이 계산된다.
- [math]\mathbf{x}_{i+1} = \mathbf{x}_i - \gamma_i \nabla f(\mathbf{x}_i)[/math]
이때 [math]\gamma_i[/math]는 이동할 거리를 조절하는 매개변수이다. (역 삼각형 기호는 그라디언트를 의미한다.)
Convergence of backprop
Perceptron은 convex optimization문제를 풀어야 한다. 이때 여러개의 global minimun (global minima-복수형)중에서 하나의 global minimum을 찾아야 한다. Mutilayer Perceptrons (MLP)는 convex하지 않는다. 따라서 Gradient decent는 local minima에서 수렴하게 된다. 그러나 이러한 local minima가 최선인지는 알 수가 없다. 즉 hyper-parameter설정이 매우 중요하게 된다. 또한 MLP에서 수렴하지 않을 수 있다. 즉 수렴성을 보장하지 않는다. 이러한 MLP를 학습시키기 위해서 back propagation이 사용된다.
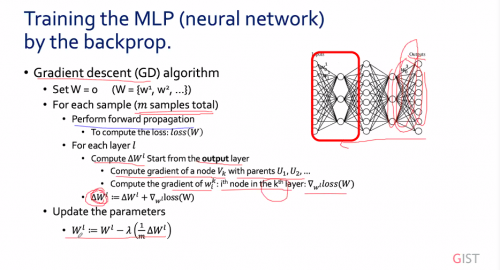
GD 알고리즘
최적화할 함수 [math]f(\mathbf{x})[/math]에 대하여, 먼저 시작점 [math]\mathbf{x}_0[/math]를 정한다. 현재 [math]\mathbf{x}_i[/math]가 주어졌을 때, 그 다음으로 이동할 점인 [math]\mathbf{x}_{i+1}[/math]은 다음과 같이 계산된다.
- [math]\mathbf{x}_{i+1} = \mathbf{x}_i - \gamma_i \nabla f(\mathbf{x}_i)[/math]
이때 [math]\gamma_i[/math]는 이동할 거리를 조절하는 매개변수이다. (역 삼각형 기호는 그라디언트를 의미한다.) 이때 인공지능에서는 이러한 GD 알고리즘을 계속해서 뒤로 Back propagation하면서 weight을 업데이트 하게 된다.