개요
Ridge 회귀모형에서는 가중치들의 제곱합(squared sum of weights)을 최소화하는 것을 추가적인 제약 조건으로 한다. L2-regularizer이라고도 불리며, Tikhonov regularization, Weight decay, SVM with hinge loss라 불리기도 한다.
- [math]w = \text{arg}\min_w \left( \sum_{i=0}^N e_i^2 + \lambda \sum_{j=1}^M w_j^2 \right)[/math]
여기서 상수항 [math]w_o[/math]는 제약조건에서 제외하게 된다.
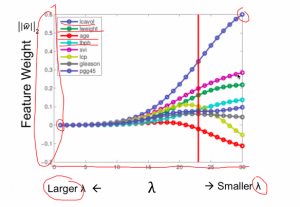
λ는 기존의 잔차 제곱합과 추가적 제약 조건의 비중을 조절하기 위한 하이퍼 모수(hyper parameter)이다. λ가 크면 정규화 정도가 커지고 가중치의 값들이 작아진다. λ가 작아지면 정규화 정도가 작아지며 λ 가 0이 되면 일반적인 선형 회귀모형이 된다.
람다의 설정
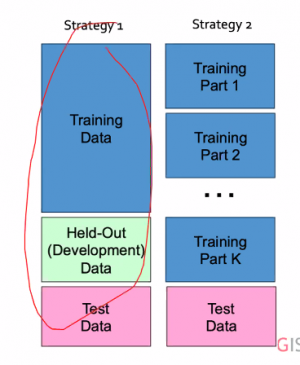
람다는 하이퍼 파라미터로 직접 설정해 주어야 한다. 이러한 람다의 설정에는 두가지 방식이 있는데, 직접 held-out set을 설정하는 방식과, tranning set을 나누어서 k-1개는 tranning에 1개는 held-out에 사용하는 k-fold방식이 있다.
참고
https://datascienceschool.net/view-notebook/83d5e4fff7d64cb2aecfd7e42e1ece5e/