개요
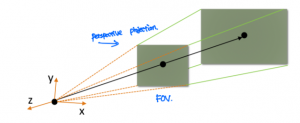
Camera Space(eye space)의 3D 오브젝트를 Canonical view volume으로 전환시키는 과정이다.
사형 변환에는 Orthographic projective와 Perspective projection의 2가지 종류가 있다. 각각 원근법을 무시, 원근법을 반영하는 사영 방식이다.
특징
축은 각각 다음을 나타낸다.
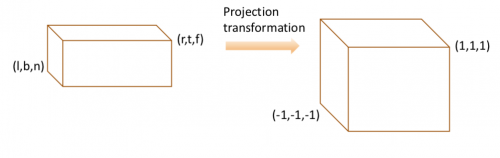
- x: l=left plane, r=right plane
- y: b=bottom plane, t=top plane
- z: n=near plane f=far plane
카메라의 위치는 원점에서 z가 작아지는 부분을 보고 있는 상황이다.
사영 변환은 주어진 카메라 좌표계에서 Canonical view volume으로 보내는 좌표계로써 Canoncial view volume은 정규화된 [-1,1][-1,1]의 크기를 가진다. 따라서 변환을 시킬때 최종적으로 얻고 싶은 이미지의 비율을 미리 고려해 주어야 한다. 만약 화면이 3대 4이라면 카메라에서 미리 3대4로 사영변환을 시켜주어야지 이미지의 비율이 깨지지 않는다. 수식으로 설명하자면 [math]\displaystyle{ \frac{화면의 x 픽셀 개수}{화면의 y픽셀 개수} = \frac{r}{t} }[/math] 으로 맞추어 주어야 aspect ratio 가 깨지지 않는다.
Orthographic Projection
특징
- 오브젝트와 시점의 상대적인 거리를 무시한다.
- 원근법이 반영되지 않아서 물체가 왜곡 되지 않고 그대로 표시된다는 장점아닌 장점이 있다.
- 대부분 사용하지 않지만, 2D게임이나 작도처럼 z값을 사용하지 않거나 사용하지 않는것이 좋을 경우 사용된다.
수식
기본 적인 행렬 변환식은 다음과 같다.

위에서 정의된 2차원 행렬 변환을 3차원으로 확장하면

이를 우리가 원하는 공간에 적용하면,
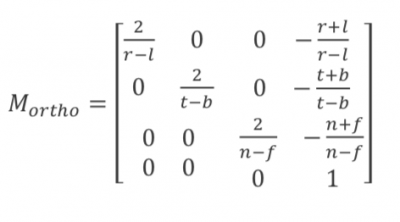
으로 정의된다.
Perspective Projection
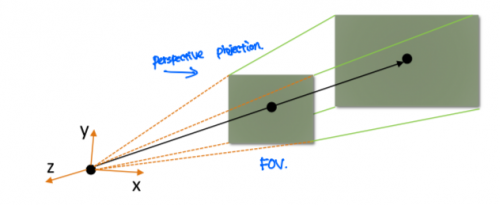
특징
- Perspective projection matrix와 앞에서 나온 결과물을 다시 orthographic transform 시킨 perspective matrix로 구성된다. 전자는 원근감을 주는 것이고 후자는 전자의 결과를 canonical space로 변환시키는 것이다.
- 오브젝트와 시점이 상대적인 거리를 반영하여 원근감을 살린다.
- 대부분의 3D모델링에서 사용한다.
수식
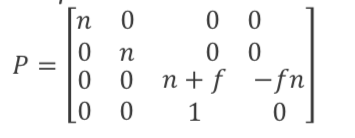
이 행렬를 사용하여 Perspective Matrix를 나타내면 다음과 같다.
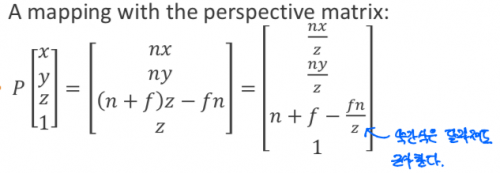
여기서 2번째 식에서 z값을 각 항들을 나누어 주면 3번째 식이 도출된다.
나누어 주는 이유는 마지막 z로 나중에 나누어 주기로 약속했기 때문이다. 즉 z로 나누어 주어 z값이 커질수록 더 작아지도록 한 것이다.
- n은 카메라 부터 near plane 까지의 거리이다. (이때 카메라의 위치가 0이기 때문에 값은 음수이지만 어차피 z 값도 음수이기 때문에 상관 없다.)
- z는 물체의 깊이 정보이다.
- z값은 나중에 Z-Buffer같은 곳에서 사용할 수도 있으니 최대한 보존해야 한다. 따라서 [math]\displaystyle{ (n+f)z -fn }[/math]로 나타내어 보존시킨다. (선형 근사의 형태이다!)
- 첫번째, 두번째, 네번째 항은 perspective 방정식을 위한 것이다.
- 세번째 항은 z를 최대한 근사시켜서 유지시키는 역활이다. z = n 이면 z의 값이 보존되고 z > n 이면 z 값이 정확히 유지되지는 않지만 순서는 유지되어서 Z-Buffer에 사용할 수 있다.
위에서 구한 식은 Perspective projection matrix로 아직 Canonical space로 보내지 않은 상태이다. 즉 우리는 한번더 Orthographic transformation을 가하여서 Canonical space로 보내야한다.
이에 따르면 전체 수식은 [math]\displaystyle{ M_{per} = M_{ortho}P_{Perspective Projection Matrix} }[/math]로 구해진다. 또한 World space에서 Screen space로 보내는 식은 [math]\displaystyle{ M_{world to screen} = M_{viewport}M_{per}M_{viewing} }[/math] 으로 정의된다.
