Regular Expressions

개요

정규 표현식(regular expression)은 문자열에서 특정한 패턴을 찾거나 치환·검증하기 위해 사용하는 표현식이다.

Formal Definition of Regular Expressions

정규 표현식 집합 [math]\displaystyle{ \mathcal{RE} }[/math]는 알파벳 집합 [math]\displaystyle{ \Sigma }[/math]에 대해 아래의 닫힘 조건(closure conditions)을 만족하는 최소 집합을 의미한다:

[math]\displaystyle{ a \in \mathcal{RE},\,\, \forall a \in \Sigma }[/math]
빈 문자열 [math]\displaystyle{ \epsilon }[/math]에 대해, [math]\displaystyle{ \epsilon \in \mathcal{RE} }[/math]
어떤 문자열도 포함하지 않는 공집합 [math]\displaystyle{ \empty }[/math]에 대해, [math]\displaystyle{ \empty \in \mathcal{RE} }[/math]
Union: If [math]\displaystyle{ R_1 \in \mathcal{RE}, R_2 \in \mathcal{RE} }[/math], then [math]\displaystyle{ (R_1 \cup R_2) \in \mathcal{RE} }[/math]
Concatenation: If [math]\displaystyle{ R_1 \in \mathcal{RE}, R_2 \in \mathcal{RE} }[/math], then [math]\displaystyle{ (R_1 \circ R_2) \in \mathcal{RE} }[/math]
Kleene Star: If [math]\displaystyle{ R_1 \in \mathcal{RE} }[/math], then [math]\displaystyle{ (R_1*) \in \mathcal{RE} }[/math]

이때 정규 표현식은 단순히 문자열(strings)이며, [math]\displaystyle{ \{\empty, \epsilon, (, ), \cup, \circ, *\} \cup \Sigma }[/math]라는 알파벳 집합 위에서 정의된다. 따라서, [math]\displaystyle{ a \cup b }[/math]라는 정규표현식이 문자열로 해석되어 단순히 알파벳 [math]\displaystyle{ a,\cup,b }[/math]의 조합인지, 혹은 정규표현식 [math]\displaystyle{ a, b }[/math]의 합집합으로 해석되는지는 맥락에 따라 달라진다.

Structural Induction for RE

어떤 성질 P(R)이 모든 정규 표현식 R에 대해 성립함을 보이고 싶다면 먼저, 아래와 같은 기본 케이스를 규정해야 한다:

1. [math]\displaystyle{ P(a), \forall a \in \Sigma }[/math] 
2. [math]\displaystyle{ P(\epsilon), P(\empty) }[/math]

이를 바탕으로 두 [math]\displaystyle{ \mathcal{RE}\,\, R_1, R_2 }[/math]에 대해 [math]\displaystyle{ P(R_1), P(R_2) }[/math]가 성립한다고 가정하면, 아래도 성립함을 보인다:

1. [math]\displaystyle{ P(R_1 \cup R_2) }[/math]
2. [math]\displaystyle{ P(R_1 \circ R_2) }[/math]
3. [math]\displaystyle{ P((R_1*)) }[/math]

이 과정을 거치면 P(R)은 모든 정규 표현식 R에 대해 참이라는 결론을 얻을 수 있다.

The Language Denoted by a Regular Expression

아래는 정규 표현식 R이 나타내는 언어 L(R)을 귀납적으로 정의한 것이다:

[math]\displaystyle{ L(a) = \{a\} }[/math] → 단일 문자열 { "a" }.
[math]\displaystyle{ L(\empty) = \empty }[/math] → 아무 문자열도 없음.
[math]\displaystyle{ L(\epsilon) = \epsilon }[/math] → 오직 빈 문자열 하나만.
[math]\displaystyle{ L(R_1 \cup R_2) = L(R_1) \cup L(R_2) }[/math]
[math]\displaystyle{ L(R_1 \circ R_2) = L(R_1) \circ L(R_2) }[/math] → R1의 문자열과 R2의 문자열을 이어붙여 생성.
[math]\displaystyle{ L(R_1*) = (L(R_1))* }[/math] → R1이 만드는 문자열들의 0번 이상의 반복.

이때 아래와 같은 중요한 정리(Lemma)가 존재한다.

 For all regular expressions R the language L(R) is a regular language.

이를 증명하기 위해서는 구조적 귀납법(Structural Induction)을 사용하며, 이를 위해 아래의 명제들을 증명해야 한다:

파일:Figure 1. NFA for .png

Figure 1. NFA for [math]\displaystyle{ L(a) }[/math]

파일:Figure 2. NFA for.png

Figure 2. NFA for [math]\displaystyle{ L(\epsilon) }[/math]

파일:Figure 3. NFA for.png

Figure 3. NFA for [math]\displaystyle{ L(\empty) }[/math]

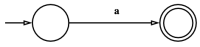
[math]\displaystyle{ \forall a \in \Sigma,\,\, L(a) }[/math] is a regular language.
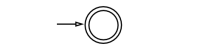
[math]\displaystyle{ L(\epsilon) }[/math] is a regular language.
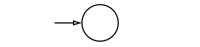
[math]\displaystyle{ L(\empty) }[/math] is a regular language.
[math]\displaystyle{ L(R1 \cup R2) = L(R1) \cup L(R2) }[/math] is a regular language.
[math]\displaystyle{ L(R1 \circ R2) = L(R1) \circ L(R2) }[/math] is a regular language.
[math]\displaystyle{ L(R1*) = (L(R1))* }[/math] is a regular language.

먼저, 명제 1, 2, 3들은 figure 1, 2, 3에 제시된 NFA를 통해 나타내어진다. 또한, 정규 언어들은 각 연산에 대해 닫혀(close)되어 있으므로, 명제 3, 4, 5번또한 성립한다고 할 수 있다.

Simplifying Operators

연산자 우선순위를 설정하여 괄호를 생략할 수 있는데, 그 순서는 [math]\displaystyle{ \cup \lt \circ \lt * }[/math](Kleene Star)와 같다. 또한 [math]\displaystyle{ \circ }[/math] 기호를 생략하여 보통 문자열 처럼 붙여 쓸 수 있다. 따라서, [math]\displaystyle{ 01* }[/math]과 같은 정규 표현식은 [math]\displaystyle{ 0\circ(1*) }[/math]과 같다. 또한 아래는 복잡한 정규 표현식을 단순화한 예시이다.

[math]\displaystyle{ R \equiv (0 \cup(1\cup(0(((0\cup1)*)0))\cup(1(((0\cup1)*)1)))) }[/math]
[math]\displaystyle{ R \equiv 0 \cup 1\cup 0(0\cup1)*0\cup1(0\cup1)*1 }[/math]

위의 예시는 사람이 읽기에 훨씬 편하도록 R을 만든 것이다. 이는 연산자 우선순위 규칙과 괄호 생략 규칙을 도입한 이유이다. [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math]

각주