Mathematical Induction

상위 문서: Mathematical Induction

개요

수학적 귀납법(Proof by Induction)은 자연수에 대한 명제를 증명할 때 주로 사용되는 증명 방법이다.

Principle of Mathematical Induction

Figure 1. Proofs by Induction

Figure 1. Proofs by Induction

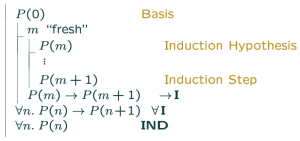
수학적 귀납법은 자연수에 대한 명제를 증명할 때 주로 사용되는 추론 규칙이다. 이의 목표는 [math]\displaystyle{ \forall n.P(n) }[/math]을 증명하는 것, 즉 모든 자연수 n에 대해 명제 [math]\displaystyle{ P(n) }[/math]이 참임을 증명하는 것이다. 귀납법은 다음 두 단계로 나뉘어진다:

1. Basis (기초 단계): [math]\displaystyle{ P(0) }[/math]을 먼저 증명한다.
2. Induction Step (귀납 단계): [math]\displaystyle{ \forall n. P(n) \rightarrow P(n+1) }[/math]임을 증명한다.

위 두 단계를 fitch-style 형식으로 정리하면 figure 1과 같은 꼴이 된다.

Complete Induction

[math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math]