Mathematical Induction

상위 문서: Mathematical Induction

개요

수학적 귀납법(Proof by Induction)은 자연수에 대한 명제를 증명할 때 주로 사용되는 증명 방법이다.

Principle of Mathematical Induction

Figure 1. Proofs by Induction

Figure 1. Proofs by Induction

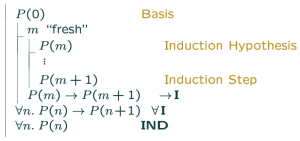
수학적 귀납법은 자연수에 대한 명제를 증명할 때 주로 사용되는 추론 규칙이다. 이의 목표는 [math]\displaystyle{ \forall n.P(n) }[/math]을 증명하는 것, 즉 모든 자연수 n에 대해 명제 [math]\displaystyle{ P(n) }[/math]이 참임을 증명하는 것이다. 귀납법은 다음 두 단계로 나뉘어진다:

1. Basis (기초 단계): [math]\displaystyle{ P(0) }[/math]을 먼저 증명한다.
2. Induction Step (귀납 단계): [math]\displaystyle{ \forall n. P(n) \rightarrow P(n+1) }[/math]임을 증명한다.

위 두 단계를 fitch-style 형식으로 정리하면 figure 1과 같은 꼴이 된다.

Complete Induction

파일:Figure 2. Complete Induction.png

Figure 2. Complete Induction

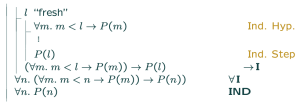
귀납법 중에는 완전 귀납법(complete induction)이 존재한다. 일반적인 귀납법과는 다르게, 완전 귀납법은 [math]\displaystyle{ P(n) }[/math]을 증명하고자 할 때, 단순히 [math]\displaystyle{ P(n-1) }[/math]만을 쓰는 것이 아니라 [math]\displaystyle{ P(0), P(1), \cdots, P(n-1) }[/math]을 가정하고 쓸 수 있다. 즉, 아래와 같은 형식적 규칙을 가진다:

[math]\displaystyle{ \frac{\forall n.(\forall m.m\lt n \rightarrow P(m)) \rightarrow P(n)}{\forall n.P(n)} }[/math]

따라서 모든 n에 대해 “n보다 작은 모든 수에 대해 성립하면 [math]\displaystyle{ P(n) }[/math]도 성립한다"가 참이면, 전체적으로 [math]\displaystyle{ \forall n.P(n) }[/math]또한 참이라는 것이다. 이는 figure 2와 같은 꼴을 통해 fitch style로 나타내어 진다.

완전 귀납법의 특징은 n번째 명제를 증명할 때, 바로 앞의 n-1 번째 명제 뿐만이 아니라 [math]\displaystyle{ P(0),P(1),\cdots,p(n-1) }[/math]을 모두 사용할 수 있다는 것이며, 이를 통해 더욱 유연한 증명을 할수 있다는 것이다. 이는 어떠한 명제 [math]\displaystyle{ P(n) }[/math]이 바로 전 단계 [math]\displaystyle{ P(n-1) }[/math]만 가지고서는 증명할 수 없기 때문에 사용된다. 예를 들어서 소인수분해 정리를 증명해야 한다고 하자:

• n이 소수가 아니면 [math]\displaystyle{ n = a \times b }[/math]꼴이며, 이때 [math]\displaystyle{ a, b \lt n }[/math]
• 따라서 [math]\displaystyle{ a, b }[/math]에 대해 이미 성립한다고 가정해야 n에 대해서도 성립한다.
• 이때 [math]\displaystyle{ P(n-1) }[/math]하나면 성립한다고 가정하는 것은 부족하며, n보다 작은 모든 값에 대해 성립한다고 가정해야 한다.

완전귀납법의 주요한 특징은 "Base Case"가 따로 필요 없다는 것이다. 왜냐하면 [math]\displaystyle{ n=0 }[/math]일 때 가정은 [math]\displaystyle{ \forall m. (m \lt 0 \rightarrow P(0)) }[/math]인데, "0보다 작은 자연수는 없다"는 명제는 항상 참이기 때문이다.

Generalized Induction Rules

귀납법이 꼭 자연수에 관한 명제에 대해서만 쓰이는 것은 아니다. 귀납법은 "비교 관계(<)"에 기초를 두고 있으므로, 일반적으로 어떠한 순서 관계가 있다면 귀납법을 정의할 수 있기 때문이다. 예를 들어 아래와 같은 공리를 살펴보자:

[math]\displaystyle{ \frac{\forall A.(\forall B.B\in A \rightarrow P(B)) \rightarrow P(A)}{\forall A. P(A)} }[/math]

이는 "집합 A의 모든 원소인 집합 B가 명제 P에 대해 성립하면 A도 성립한다"라는 의미이다. 이를 [math]\displaystyle{ \in }[/math]-귀납법([math]\displaystyle{ \in }[/math]-induction)이라고 부른다. 이 귀납법은 비교 관계로 "부등호(<)"가 아닌 "엡실론([math]\displaystyle{ \in }[/math])"을 사용한다. 즉, 이는 “어떤 집합의 원소가 그 집합보다 더 작다"라는 개념을 순서 관계로 보는 것이다.

Well-Founded Induction

귀납법은 "비교 관계(<)"가 잘 정의(well-founded) 되었을 때 일반화될 수 있다. 어떤 비교 관계가 잘 정의되었다는 것의 정의는 아래와 같다:

어떤 집합 A위의 관계 <가 well-founded라면, 빈 집합이 아닌 모든 부분집합 B는 최소 원소를 가진다.

즉, 자연수 집합의 경우에는 [math]\displaystyle{ 5 \gt 4 \gt 3 \gt 2 \gt 1 }[/math]과 같이 끝이 있으니 잘 정의된다. 하지만 정수를 생각해보면, [math]\displaystyle{ 2 \gt 1 \gt 0 \gt -1 \gt -2 \gt ... }[/math]과 같이 최소 원소가 정의되지 않기 때문에 잘 정의되지 않는다. 이는 양의 실수에도 동일하게 적용되어, 잘 정의되지 않는다는 것을 알 수 있다.

만약 <가 well-founded라면 아래와 같은 귀납 원리가 성립한다:

[math]\displaystyle{ \frac{\forall x. (\forall y. (y\lt x \rightarrow P(y))\rightarrow P(x))}{\Rightarrow \forall x.P(x)} }[/math]

이는 "어떤 원소 x에 대해, x보다 작은 모든 y에서 성립하면 x도 성립한다"면, 전체적으로 모든 원소에 대해 성립한다는 의미이다.

이는 자연수 뿐만 아니라 다양한 구조에 적용가능하다. 집합 관계에는 [math]\displaystyle{ \in }[/math]을, 문자열에는 적절한 접두사 관계를 사용할 수 있다. 표현식 트리(expression trees)에서는 "부분식(subexpression)" 관계를 사용할 수 있다.

Inductively Defined Sets

귀납적으로 정의된 집합(Inductively Defined Sets)은 어떤 집합을 한번에 다 정의하는 대신, 규칙(closure conditions)을 정해서 그 규칙을 만족하는 원소들만 집합에 포함시키는 방식이다. 예를 들어서 식(Expression) 집합을 정의해보자.

1. 기본 원소(Base Case): 문자 a 하나만 있어도 그것은 식(expression)이다.
2. 덧셈 규칙(Closure under +): [math]\displaystyle{ E_1, E_2 }[/math]가 식이면 [math]\displaystyle{ (E_1 + E_2) }[/math]또한 식이다.
3. 곱셈 규칙(Closure under [math]\displaystyle{ \cdot }[/math]): [math]\displaystyle{ E_1, E_2 }[/math]가 식이면 [math]\displaystyle{ (E_1 \cdot E_2) }[/math]또한 식이다.
4. 최소성 조건(Smallest set): 위 규칙을 유한 번 적용해서 만들 수 있는 것만 식이다.

Structural Induction

구조적 귀납법(Structural Induction)은 귀납법으로 정의된 집합에 대해 사용되는 귀납법이다. 이는 "집합 원소의 생성 규칙"을 기반으로 하는 귀납법이다. 예를 들어서 식(Expression)에 대한 구조적 귀납법을 관찰하자:

1. 기본 단계(Basis): 문자 a에 대해 [math]\displaystyle{ P(a) }[/math]가 성립함을 보인다.
2. 귀납 단계(덧셈): 만약 [math]\displaystyle{ E_1, E_2 }[/math]에 대해 [math]\displaystyle{ P(E_1), P(E_2) }[/math]가 참이면, [math]\displaystyle{ P(E_1 + E_2) }[/math]도 참임을 보인다.
3. 귀납 단계(곱셈): 만약 [math]\displaystyle{ E_1, E_2 }[/math]에 대해 [math]\displaystyle{ P(E_1), P(E_2) }[/math]가 참이면, [math]\displaystyle{ P(E_1 \cdot E_2) }[/math]도 참임을 보인다.

이렇게 하면 식의 전체 집합에 대해 [math]\displaystyle{ P(E) }[/math]가 항상 성립한다고 말할 수 있다.