시스톨릭 배열

개요

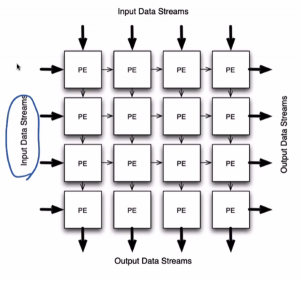
Dataflow machine과 같은 병렬 처리에 특화된 구조는 특별한 시스템을 사용해서 명령을 처리하게 된다. 이중 하나의 방법이 시스톨릭 배열 (Systolic array)이다. TPU와 같은 아키텍쳐에서 사용되며, 크게 입력 데이터 -> 출력 데이터의 구조를 가지고 있다.

시스톨릭 어레이는 데이터가 배열 형태로 배치되어 있고, 각 셀은 데이터를 연산하고 다음 셀로 전달한다. 이때 데이터는 한 방향으로만 흐르며, 이러한 특성 때문에 "시스톨릭"이라는 용어가 사용된다. 각 셀은 일반적으로 작고 간단한 연산을 수행하며, 전체적인 성능은 병렬로 동작하는 여러 셀의 조합에 의해 결정된다. 시스톨릭 어레이는 주로 행렬 곱셈이나 컨벌루션과 같은 수학적인 연산에 사용되며, 고성능 및 효율적인 에너지 사용을 위해 설계된다. 또한, 신호 처리 및 이미지 처리와 같은 응용 분야에서도 널리 사용된다.

HB (heart beat)신호가 들어오면 각각의 Processing element(PE)가 전단계에서 들어온 정보에 특정한 연산을 가하고 다음 PE로 신호를 전달한다. 이러한 방식으로 계속해서 신호를 각각의 PE연산자가 계산하면 최종 결과가 도출된다. 거의 그리고 어쩌면 오직 인공지능에서만 사용되는데, 이는 이 기법을 통해서 계산할 수 있는 방법이 매우 제한적이지만 행렬의 dot product계산에 최적화된 성능을 발휘 할 수 있기 때문이다. 어쩌면 Pipeline과 비슷하지만 이러한 경로가 linear하지 않고 nonlinear이며 그리고 multidirectional이라는 것이 차이점이다.

예시

시스톨릭 어레이는 데이터를 효율적으로 처리하기 위해 여러 개의 셀이 일렬로 배치된 구조이다. 이를 이해하기 위해 행렬 곱셈 연산을 예시로 들수 있다. 예를 들어, 두 개의 행렬 A와 B가 있고, 이를 곱하여 결과 행렬 C를 얻고자 하면, 이때 각 행렬은 다음과 같이 표현될 수 있다.

\[ A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ \end{bmatrix}, \quad B = \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \\ b_{31} & b_{32} \\ \end{bmatrix} \]

여기서 [math]a_{ij}[/math]와 [math]b_{ij}[/math]는 각 행렬의 원소를 나타낸다. 이제 시스톨릭 어레이를 사용하여 이 두 행렬을 곱해보자.

시스톨릭 어레이에서는 각 셀이 하나의 연산을 수행하고, 데이터가 한 방향으로만 흐른다고 하였다. 따라서 행렬 A의 각 행과 B의 각 열을 시스톨릭 어레이의 입력으로 사용할 수 있다. 이때 한 번의 연산은 한 번의 클록 사이클(HB)에 이루어진다.

예를 들어, A의 첫 번째 행과 B의 첫 번째 열을 처리하는 경우, 시스톨릭 어레이의 첫 번째 셀에서는 [math]a_{11} \times b_{11}[/math]을 계산하고, 다음 셀에서는 [math]a_{12} \times b_{21}[/math]을 계산하며, 이런 식으로 데이터가 전달된다. 그리고 결과는 다시 한 층씩 내려오면서 합산되어 결과 행렬 C의 첫 번째 원소가 만들어진다.

이러한 방식으로, 시스톨릭 어레이는 행렬 곱셈과 같은 연산을 병렬로 처리하고, 각 셀이 매우 간단한 연산만을 수행하기 때문에 고성능을 제공한다. 이는 대규모 데이터 집합에 대한 병렬 처리에 매우 효과적이다. 특히 각각의 셀의 연산이 간다하며 효율적이기 때문에 Systolic array들을 이론상 Scalable하게 펼치는 것이 가능하다. 따라서 아키텍쳐 적으로도 병렬처리에 특화되어 있다.