Nondeterministic Finite Automata

상위 문서: Finite Automata

개요

해당 문서는 finite automata의 한 종류인 NFA(Nondeterministic Finite Automata)에 대해 설명하고, 이를 이용한 정규 언어의 정의 방식을 설명한다.

NFA Vs. DFA

DFA(Deterministic Finite Automata)에서는 각 상태와 입력 심볼 쌍 (q, a)에 대해 오직 하나의 전이만 정의된다. 하지만 NFA에서는 하나의 (q,a)에 대해 여러 개의 전이가 있을 수도 있고, 전이가 전혀 없을 수도 있으며, 입력을 소모하지 않고 이동하는 ε-transition도 허용된다. 이때 수용(accept) 조건은 어떤 행운의 선택(lucky choice)"의 전이 경로라도 최종 상태에 도달하면 문자열을 accept하는 것이다.

파일:Figure 1. NFA example .png

Figure 1. NFA example

이는 figure 1을 통해 설명할 수 있다. 주어진 NFA는 {0,1} 위의 문자열을 입력받아, 끝에서 세 번째 문자가 1인 문자열을 accept한다. 이러한 NFA는 아래와 같은 방식으로 작동한다:

1. 계속해서 Q1에서 입력을 소비하다가,
2. 어느 순간 "여기가 끝에서 세 번째 자리일 것"이라고 추측(guess)하고 Q2로 이동.
3. 그 뒤 정확히 두 개 문자를 더 읽고 Q4에 도착하면 accept.
4. 만약 모든 "선택과 추측"이 실패하면, 해당 문자열을 수용되지 않음

Formal Definition of NFA

NFA는 DFA 처럼 아래와 같은 5-튜플로 정의된다:

• [math]\displaystyle{ Q }[/math]: 유한 상태 집합
• [math]\displaystyle{ \Sigma }[/math]: 유한 입력 기호 집합(입력 알파벳)
• [math]\displaystyle{ \delta }[/math]: [math]\displaystyle{ Q\times (\Sigma \cup \{\epsilon\} \rightarrow \mathcal{P}(Q)) }[/math]: 전이 함수(transition function)
  • 이는 DFA의 그것과는 다르게 “다음 상태 하나”가 아니라 “가능한 다음 상태들의 집합”을 반환한다.
  • ε-transition이 발행하여 입력 문자를 읽지 않고도 상태가 바뀔 수 있다.
• [math]\displaystyle{ q_0 \in Q }[/math]: 시작 상태(start state)
• [math]\displaystyle{ F \subseteq Q }[/math]: 수용 상태 집합(a set of accept states)

Formal Definition of the Language Recognized by NFA

문자열 [math]\displaystyle{ w \in \Sigma* }[/math]를 NFA [math]\displaystyle{ M }[/math]이 accept한다는 것은 아래와 같이 정의된다:

• [math]\displaystyle{ w }[/math]를 [math]\displaystyle{ w=y_1y_2\cdots y_n }[/math](각 [math]\displaystyle{ y_i\in \Sigma \cup \{\epsilon\} }[/math])로 분해가능하고,
• 상태열 [math]\displaystyle{ r_0,r_1,\cdots,r_n }[/math]이 존재하여:
  • [math]\displaystyle{ r_0=q_0 }[/math] (시작 상태)
  • [math]\displaystyle{ r_{i+1} \in \delta(r_i, y_{i+1}) }[/math] (전이 규칙을 따름)
  • [math]\displaystyle{ r_n \in F }[/math] (accept 상태 도달)

이를 만족하는 모든 문자열들의 집합이 [math]\displaystyle{ L(M) }[/math]이다.

Proof for Closure

NFA를 이용하여 정규 언어의 기본 연산 폐쇄성(closure)를 증명할 수 있다.

Closure under Union

증명해야 하는 것은 아래와 같다:

Figure 2. Closure under Union

Figure 2. Closure under Union

[math]\displaystyle{ \forall A_1, A_2.\,\, (A_1\,\, regular \land A_2\,\, regular) \Rightarrow (A_1 \cup A_2\,\, regular) }[/math]

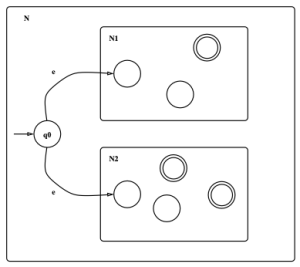
1. 이를 위해 [math]\displaystyle{ A_1, A_2 }[/math]를 인식하는 NFA [math]\displaystyle{ N_1, N_2 }[/math]가 있다고 가정하자.
2. 새로운 NFA [math]\displaystyle{ N }[/math]을 하나 만든다.
3. N은 새로운 시작 상태 [math]\displaystyle{ q_0 }[/math]를 갖고, 여기서 ε-transition으로 [math]\displaystyle{ N_1,\,\, N_2 }[/math]의 시작 상태로 이동한다.
4. 그러면 [math]\displaystyle{ N }[/math]은 [math]\displaystyle{ N_1 }[/math] 혹은 [math]\displaystyle{ N_2 }[/math] 중 하나를 실행하여 문자열을 수용한다.
5. 따라서 [math]\displaystyle{ N }[/math]이 인식하는 언어는 정확히 [math]\displaystyle{ A_1 \cup A_2 }[/math]이다.

Closure under Concatenation

증명해야 하는 것은 아래와 같다:

파일:Figure 3. Closure under Concatenation.png

Figure 3. Closure under Concatenation

[math]\displaystyle{ \forall A_1, A_2.\,\, (A_1\,\, regular \land A_2\,\, regular) \Rightarrow (A_1 \circ A_2\,\, regular) }[/math]

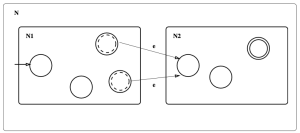
1. 이를 위해 [math]\displaystyle{ A_1, A_2 }[/math]를 인식하는 NFA [math]\displaystyle{ N_1, N_2 }[/math]가 있다고 가정하자.
2. 새로운 NFA [math]\displaystyle{ N }[/math]을 하나 만든다.
3. [math]\displaystyle{ N }[/math]은 [math]\displaystyle{ N_1 }[/math]의 시작 상태에서 시작한다.
4. 그리고 [math]\displaystyle{ N_1 }[/math]의 accept된 상태들에서 ε-transition을 통해 [math]\displaystyle{ N_2 }[/math]의 시작 상테로 넘어간다.
5. 이 경우 [math]\displaystyle{ N }[/math]은 먼저 [math]\displaystyle{ A_1 }[/math]에 속하는 문자열을 인식하고, 그 다음 [math]\displaystyle{ A_2 }[/math]의 문자열을 인식한다.
6. 따라서 [math]\displaystyle{ N }[/math]은 [math]\displaystyle{ A_1 \circ A_2 }[/math]를 인식하게 된다.

Closure under Star

증명해야 하는 것은 아래와 같다:

파일:Figure 4. Closure under Star.png

Figure 4. Closure under Star

[math]\displaystyle{ A*\circ A \subseteq A* }[/math]

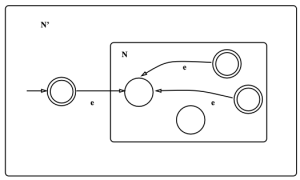
1. 이를 위해 [math]\displaystyle{ A }[/math]를 인식하는 NFA [math]\displaystyle{ N }[/math]이 있다고 가정하자.
2. [math]\displaystyle{ A* }[/math]를 인식하는 NFA [math]\displaystyle{ N' }[/math]을 만든다.
3. [math]\displaystyle{ N' }[/math]은 새로운 시작 상태와 새로운 accept 상태를 가진다.
4. 새 시작 상태에서 ε-transition으로 바로 [math]\displaystyle{ N }[/math]의 시작 상태나, 또는 새 accept 상태로 갈 수 있다.(→ 빈 문자열도 받아들임)
5. [math]\displaystyle{ N }[/math]의 accept 상태들은 다시 ε-transition을 통해 [math]\displaystyle{ N }[/math]의 시작 상태나 최종 accept 상태로 갈 수 있다. (→ 여러 번 반복 가능)