Triangle rasterization

개요

3D 그래픽스에서 각각의 vertex들이 주어졌을때 이를 포함하는 픽셀들을 그려나가는 방식중 하나이다.

셰이더 없는 상황

Gouraud Interpolation 이라고 부르는 레스터라이제이션은 제일 기본적인 레스터화 방식중 하나이다.

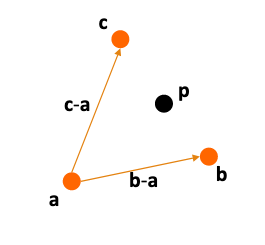
점 a, b, c가 주어진 상황에서 픽셀 p의 값을 계산하기 위해

[math]p[/math]를 기준으로 하는 선분 방정식을 세우면, 다음과 같다.

[math] p = a + \beta(b-1)+\gamma(c-a) [/math] 를 정리하여

[math] p(\alpha,\beta,\gamma) = \alpha a+\beta b+\gamma c\space(\alpha = 1-\beta-\gamma)[/math]

[math] p(\alpha,\beta,\gamma) = \alpha a+\beta b+\gamma c\space(\alpha+\beta+\gamma = 1)[/math]

이때 [math] \alpha, \beta, \gamma [/math]가 모두 0과 1 이내의 범위에 있으면 p는 삼각형 내부에 포함되는 것으로 픽셀을 그리면 된다.

문자는 3개지만 [math]\alpha[/math]는 [math]\alpha = 1-\beta-\gamma[/math]로 주어지기 때문에 자동으로 구해진다.

따라서 [math] \alpha, \beta, \gamma [/math]는 x에 관한 식과 y에 관한식 두개를 연립하여 구하면 된다.

구해진 [math]\alpha, \beta, \gamma [/math]에 대해서 픽셀 c 를 [math] c = \alpha c_0+\beta c_1+\gamma c_2 [/math]로 표현하여 색칠하면 된다.

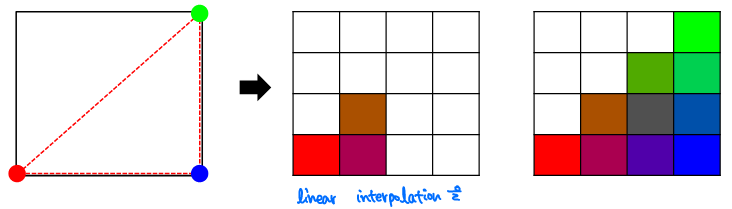
전체적인 작동 방식은 다음과 같다.