다른 명령
편집 요약 없음 |
잔글 봇: 자동으로 텍스트 교체 (-\[\[분류:컴퓨터 공학(\|[^\]]+)?\]\] +) |
||
| (다른 사용자 한 명의 중간 판 25개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
[[분류:계산 이론 개론]] | [[분류:계산 이론 개론]] | ||
상위 문서: [[Grammars#Context-Free Languages | 상위 문서: [[Grammars#Context-Free Languages|Context-Free Languages]] | ||
==개요== | ==개요== | ||
| 11번째 줄: | 11번째 줄: | ||
# 이후 입력의 나머지 부분을 읽으며, 스택에서 pop한 심볼과 비교한다. | # 이후 입력의 나머지 부분을 읽으며, 스택에서 pop한 심볼과 비교한다. | ||
# 모두 일치하고 스택이 비면 해당 문자열은 PDA에 의해서 accept된다. | # 모두 일치하고 스택이 비면 해당 문자열은 PDA에 의해서 accept된다. | ||
이때, 모든 NFA는 PDA의 특수한 경우로 볼 수 있다. 왜냐하면 PDA는 스택을 가진 오토마타지만, 스택을 전혀 사용하지 않게 정의하면 그건 곧 NFA와 동일한 동작을 하기 때문이다. 이를 통해서 아래와 같은 명제가 성립한다: | |||
Context-Free Languages <math>\supseteq</math> Regular Languages | |||
==Formal Definition of nondeterministic PDA== | ==Formal Definition of nondeterministic PDA== | ||
| 17번째 줄: | 19번째 줄: | ||
* <math>\Sigma</math>: 입력 알파벳 | * <math>\Sigma</math>: 입력 알파벳 | ||
* <math>\Gamma</math>: 스택 알파벳 | * <math>\Gamma</math>: 스택 알파벳 | ||
* <math>\delta</math>: | * <math>\delta</math>: <math>\delta: Q\times \Sigma_\epsilon \times \Gamma_\epsilon \rightarrow P(Q\times \Gamma_\epsilon)</math> | ||
** 전이 함수(transition function)로, 현재 상태와 입력 기호를 다음 상태로 매핑한다. | |||
** 현재 상태, 입력 알파벳, 스택의 top 알파벳에 따라 여러 <math>(r,b) \in \delta(q,w,a)</math> 쌍을 반환한다. | ** 현재 상태, 입력 알파벳, 스택의 top 알파벳에 따라 여러 <math>(r,b) \in \delta(q,w,a)</math> 쌍을 반환한다. | ||
* <math>q_0 \in Q</math>: 시작 상태(start state) | * <math>q_0 \in Q</math>: 시작 상태(start state) | ||
| 38번째 줄: | 40번째 줄: | ||
===Computation Example=== | ===Computation Example=== | ||
[[파일:Figure 1. PDA Example 1.png|섬네일|Figure 1. PDA Example 1]] | |||
Figure 1은 아래 언어를 나타내는 언어의 구현을 나타낸 것이다: | Figure 1은 아래 언어를 나타내는 언어의 구현을 나타낸 것이다: | ||
<math>L = \{a^ib^jc^k|i,j,k \ge 0 \and (i = j \lor i = k)\}</math> | <math>L = \{a^ib^jc^k|i,j,k \ge 0 \and (i = j \lor i = k)\}</math> | ||
| 47번째 줄: | 50번째 줄: | ||
# <math>q_4</math>: i=k이므로 수용 상태에 계속 머무른다. | # <math>q_4</math>: i=k이므로 수용 상태에 계속 머무른다. | ||
# <math>q_5\sim q_7</math>: 다른 경로 (nondeterminism)로 두 경우 모두 처리 가능하도록 설계. | # <math>q_5\sim q_7</math>: 다른 경로 (nondeterminism)로 두 경우 모두 처리 가능하도록 설계. | ||
<math></math> | |||
<math></math> | ==PDA and CFG== | ||
<math></math> | ===PDA’s from CFG’s=== | ||
<math></math> | 모든 CFG는 어떤 PDA에 의해 인식되며, 이는 CFG→PDA 변환이 가능하다는 뜻이다. 이때 CFG를 PDA로 변환하는 것은 아래와 같이 스택을 이용하여 실현된다: | ||
# 스택은 아직 남은 입력 문자열을 도출하기 위해 필요한 문장형식(sentential form)을 유지한다. | |||
#* CFG에서 문장을 생성할 때에는 "시작 비단말기 S"에서 여러 변환 규칙을 걸치면서 생성된다. | |||
#* PDA에서는 스택에 그 현재 문장형식(예: <math>S \rightarrow aSb \rightarrow aabb</math>) 의 “아직 처리되지 않은 부분”을 저장한다.<ref>즉, 스택은 “현재 어디까지 유도했는지”를 나타낸다.</ref> | |||
# 스택의 top에 단말기가 있을 때, 그것이 현재 입력 문자열의 첫 글자와 비교한다. | |||
#* 두 문자가 같다면 스택에서 pop하고 입력에서도 consume한다. | |||
#* 같지 않다면 PDA의 그 “계산 경로(computation path)”는 실패한다. | |||
# 만약 스택의 top이 비단말기라면, CFG의 생성 규칙 중 하나를 비결정적(nondeterministically) 선택한다. | |||
#* 만약 선택된 생성 규칙이 <math>A \rightarrow aBb</math>라면, 스택의 top인 <math>A</math>를 pop하고, <math>b,B,a</math>를 역순으로 push한다. | |||
# 스택의 내용이 다 처리되어 비면<ref>스택의 top이 $기호인 경우이다.</ref> PDA는 accept state 로 이동한다.<ref>이는 모든 입력이 정확히 문법으로부터 생성될 수 있다는 뜻이다.</ref> | |||
====PDA's states==== | |||
CFG에서 만든 PDA는 아래와 같은 세 가지 핵심적인 상태를 가진다: | |||
# <math>q_{start}</math>: 시작 상태 | |||
#* 스택에 <math>$S</math>를 push한다.<ref><math>S</math>는 시작 비단말이고, $는 스택의 바닥을 표시한다.</ref> | |||
#* 다음 상태는 <math>q_{loop}</math>이다. | |||
# <math>q_{loop}</math>: 반복 상태 | |||
#* 스택의 top이 단말기면 입력과 비교하여 “match” 후 pop한다. | |||
#* 스택의 top이 비단말기면 CFG의 생성 규칙 중 하나를 비결정적으로 선택하여 스택을 확장한다. | |||
#* 스택의 top이 $이면 <math>q_{accept}</math>로 이동 | |||
# <math>q_{accept}</math>: Accept 상태 | |||
#* 스택이 완전히 비고 입력이 끝난 상태이다. | |||
이때 만약 여러 symbol을 한꺼번에 push해야 할 때는, “extra states”를 임시로 만들어 연속 push를 구현한다. | |||
====PDA from CFG Example==== | |||
[[파일:Figure 2. PDA Example 2.png|섬네일|Figure 2. PDA Example 2]] | |||
아래와 같은 CFG가 주어졌다고 가정해보자: | |||
<math>S \rightarrow aTb | b</math> | |||
<math>T \rightarrow Ta|\epsilon</math> | |||
이를 구현하기 위해서는 <math>q_{start}, q_{loop}, q_{accept}</math>를 구현해야 하며, 스택을 CFG 규칙에 맞추어 조작해야 한다. 이는 figure 2를 관찰하면 어떻게 구현이 되었는지 잘 이해할 수 있다. | |||
===CFG’s from PDA’s=== | |||
모든 PDA는 어떤 CFG를 생성하는데, 이는 PDA→CFG 변환이 가능하다는 뜻이다. 이를 CFG의 비단말기는 <math>A_{pq}</math> 형태로 만든다.<ref>p, q는 PDA의 상태 집합의 원소이다.</ref> 이때 아래의 식이 성립한다: | |||
<math>A_{pq} \Rightarrow* w \Leftrightarrow </math>PDA가 입력되는 w를 읽으면서 상태 p에서 q로 이동하고, 스택이 완전히 비워짐 | |||
즉, CFG의 규칙은 PDA의 이동경로를 기반으로 구성된다. 또한 아래는 CFG를 만들기 위한 PDA 단순화 전제이다: | |||
# PDA P는 정확히 하나의 Accept 상태 <math>q_{accept}</math> 만을 가진다. | |||
# Accept 상태에 도달하기 위해서는 스택이 완전히 비워져야 한다. | |||
# 각 전이함수는 push 하나 또는 pop 하나만 수행한다. | |||
====Definition of G==== | |||
위의 내용을 사용하여 CFG를 구체적으로 아래와 같이 정의한다: | |||
# 변수 집합: <math>V = \{A_{pq}|p,q \in Q\}</math> | |||
#* 각 변수는 PDA의 상태 p에서 시작해, 상태 q에서 끝나는 모든 문자열들을 생성하는 비단말기를 의미한다.<ref>쉽게 말하면, “상태 p에서 시작해서 q로 갈 수 있는 입력 문자열”을 대표하는 문법 기호이다.</ref><ref>다르게 설명하면, 상태 p에서 상태 q로 이동하는 과정에서 스택의 상태가 처음과 같게 유지되는 모든 문자열들의 집합을 의미한다.</ref> | |||
# 시작 변수: <math>S = A_{q_0q_{accept}}</math><ref>PDA의 시작 상태 <math>q_0</math>에서 accept 상태까지 가는 문자열을 생성해야 하므로, 문법의 시작기호는 이렇게 설정됩니다.</ref> | |||
# 생성 규칙: “u를 스택에 넣고 다시 꺼내는 과정 사이에 있는 계산 전체”를 문법 규칙 하나로 표현한다: | |||
## <math>(r,u)\in \delta(p,a,\epsilon) \land (q,\epsilon) \in \delta(s,b,u)</math>이면 <math>A_{pq} \rightarrow aA_{rs}b</math>이다.<ref>p에서 q로 가는 계산은 a를 읽고 u를 푸시한 뒤, 중간에 r에서 s로 이동하면서 u를 팝하며 b를 읽는다는 것을 나타낸다.</ref> | |||
## <math>A_{pr} \rightarrow A_{pq}A_{qr}</math> | |||
## <math>A_{pp} \rightarrow \epsilon</math><ref>같은 상태에서 아무 동작 없이 스택이 빈 경우이다.</ref> | |||
이러한 규칙을 통해 CFG가 PDA의 “스택 조작 기반 계산 경로”를 그대로 재현할 수 있다. | |||
===CFG from PDA Example=== | |||
[[파일:Figure 3. CFG from PDA Example.png|섬네일|250x250픽셀|Figure 3. CFG from PDA Example]] | |||
Figure 3에서 CFG는 아래와 같이 유도된다: | |||
<math>A_{14}\rightarrow A_{23}</math> ($를 push한 후, $를 pop) | |||
<math>A_{23}\rightarrow 0A_{23}1</math> (0을 push한 후, 0을 pop) | |||
<math>A_{23}\rightarrow 0A_{22}1</math> (0을 push한 후, 0을 pop) | |||
<math>A_{22}\rightarrow \epsilon</math> | |||
위에서 <math>A_{14}</math>는 PDA의 시작 상태 <math>q_1</math>에서 accept 상태 <math>q_4</math>까지 가는 모든 입력 문자열을 생성하는 비단말기이다. 따라서 해당 비단말기는 주어진 PDA가 인식하는 언어 전체를 생성해야 하므로 <math>S=A_{14}</math>가 PDA로부터 정의되는 문법의 시작 기호 역할을 한다. | |||
<math>A_{14}\rightarrow A_{23}</math>과 같은 규칙은 아래의 두 전이: | |||
<math>(q_1,\epsilon,\epsilon)\rightarrow (q_2,$)</math> | |||
<math>(q_3,\epsilon,$)\rightarrow (q_4,\epsilon)</math> | |||
을 $에 대한 push와 pop의 짝으로 연결한 것이다. 첫 단계에서는 스택에 $를 push하며, 마지막 단계에서는 $를 스택에서 pop한다. 이에 따라 <math>A_{23}</math>는 두 단계 사이의 계산, 즉 PDA의 <math>q_2</math>에서 <math>q_3</math>까지의 계산을 의미하는 비단말기이다. 즉, <math>A_{14}\rightarrow A_{23}</math> 규칙은 <math>q_1</math>에서 $를 push하는 것으로 시작해 <math>q_4</math>에서 $를 pop하며 끝나는 전체 계산은 <math>q_2</math>에서 <math>q_3</math> 사이에서의 계산과 같다는 것을 의미한다. | |||
<math>A_{23}\rightarrow 0A_{23}1</math>과 같은 규칙은 아래의 두 전이: | |||
<math>(q_2,0,\epsilon)\rightarrow (q_2,0)</math> | |||
<math>(q_3,1,0)\rightarrow (q_3,\epsilon)</math> | |||
을 0에 대한 push와 pop의 짝으로 연결한 것이다. 또한 <math>A_{23}\rightarrow 0A_{22}1</math>과 같은 규칙은 아래의 두 전이: | |||
<math>(q_2,0,\epsilon)\rightarrow (q_2,0)</math> | |||
<math>(q_2,1,0)\rightarrow (q_3,\epsilon)</math> | |||
을 0에 대한 push와 pop의 짝으로 연결한 것이다. 이때 다른 두 비단말기에 비해 이질적인 <math>A_{22}</math>은 그 정의에 따르면 PDA가 <math>q_2</math>에서 시작해서 다시 <math>q_2</math>로 돌아오는 과정에서 스택의 상태가 처음과 같게 유지되는 모든 문자열들의 집합을 표현하는 비단말기이다. 이에 따라 스택이 유지되기 위해서는 push와 pop의 수가 같아야 하므로, <math>A_{33}</math>에서 유도될 수 있는 문자열은 <math>\epsilon</math> 뿐이다. | |||
==각주== | ==각주== | ||
2026년 1월 15일 (목) 15:23 기준 최신판
상위 문서: Context-Free Languages
개요
정규 언어를 다루기 위해서는 FA(Finite Automaton)으로 충분하지만, 그보다 더 일반적인 언어인 CFG(Context-Free Languages)를 다루기 위해서는 PDA(Pushdown Automaton)[1]>가 사용된다. PDA는 FA의 한계를 보완하기 위해서 추가적인 기억 장치인 stack을 활용하며, 이를 통해서 추가적인 '기억'을 구현할 수 있다. 예를 들어 아래와 같은 언어를 고려해보자:
[math]\displaystyle{ L = \{ww^R|w\in\Sigma*\} }[/math]
이는 아래와 같은 작동 과정을 거친다:
- 입력의 앞부분 w를 스택에 차례로 push 한다.
- w가 끝났다고 nondeterministically guess(추측)한다.
- 이후 입력의 나머지 부분을 읽으며, 스택에서 pop한 심볼과 비교한다.
- 모두 일치하고 스택이 비면 해당 문자열은 PDA에 의해서 accept된다.
이때, 모든 NFA는 PDA의 특수한 경우로 볼 수 있다. 왜냐하면 PDA는 스택을 가진 오토마타지만, 스택을 전혀 사용하지 않게 정의하면 그건 곧 NFA와 동일한 동작을 하기 때문이다. 이를 통해서 아래와 같은 명제가 성립한다:
Context-Free Languages [math]\displaystyle{ \supseteq }[/math] Regular Languages
Formal Definition of nondeterministic PDA
PDA는 아래와 같은 5-튜플([math]\displaystyle{ Q, \Gamma, \Sigma, \delta, q_0, F }[/math])로 정의할 수 있다:
- [math]\displaystyle{ Q }[/math]: 유한 상태 집합
- [math]\displaystyle{ \Sigma }[/math]: 입력 알파벳
- [math]\displaystyle{ \Gamma }[/math]: 스택 알파벳
- [math]\displaystyle{ \delta }[/math]: [math]\displaystyle{ \delta: Q\times \Sigma_\epsilon \times \Gamma_\epsilon \rightarrow P(Q\times \Gamma_\epsilon) }[/math]
- 전이 함수(transition function)로, 현재 상태와 입력 기호를 다음 상태로 매핑한다.
- 현재 상태, 입력 알파벳, 스택의 top 알파벳에 따라 여러 [math]\displaystyle{ (r,b) \in \delta(q,w,a) }[/math] 쌍을 반환한다.
- [math]\displaystyle{ q_0 \in Q }[/math]: 시작 상태(start state)
- [math]\displaystyle{ F \subseteq Q }[/math]: 수용 상태 집합(a set of accept states)
이때 전이함수는 nondeterministic PDA 위에서 정의되므로 주어진 전이 함수 [math]\displaystyle{ \delta(q,w,a) }[/math]는 여러 [math]\displaystyle{ (r,b) }[/math] 쌍을 가질 수 있다. 이때 [math]\displaystyle{ (r,b) \in \delta(q,w,a) }[/math]는 현재 상태가 q이고, 입력 알파벳이 w, 스택의 top 알파벳이 a일 때, 상태 r로 전이하며 스택에서 a를 pop하고 b를 push한다는 것을 의미한다. 만약 [math]\displaystyle{ (r,b) \in \delta(q,w,a) }[/math]에서 [math]\displaystyle{ a = \epsilon }[/math]이면 스택을 pop하지 않는 것이고, [math]\displaystyle{ b = \epsilon }[/math]이라면 스택에 push하지 않는 것이다. 이때 PDA의 스택이 비었는지를 직접 검사하는 것은 불가능하지만, 특수기호 $ 를 스택 바닥에 push하여 비어있음을 간접적으로 확인할 수 있다.
Computation of a PDA
PDA P가 입력 [math]\displaystyle{ w = w_1w_2\cdots w_m }[/math]을 수용(accept)한다는 것은 일련의 상태열 [math]\displaystyle{ r_0,r_1,\cdots r_m }[/math]과 스택 문자열열 [math]\displaystyle{ s_0,s_1,\cdots,s_m }[/math]이 존재해야 한다. 이를 위한 조건은 아래와 같다:
- [math]\displaystyle{ r_0=q_0, s_0=\epsilon }[/math]: PDA는 처음에 초기 상태 [math]\displaystyle{ q_0 }[/math]에서 시작하고 스택이 비어있다.
- For [math]\displaystyle{ i=0,1,\cdots,m-1 }[/math], [math]\displaystyle{ (\exist a_i,b_i \in \Gamma_\epsilon) \land (t \in \Gamma*) }[/math] such that ([math]\displaystyle{ s_i=a_it, s_{i+1}=b_it) \land ((r_{i+1},b_i)\in
\delta(r_i,w_{i+1}, a_i)) }[/math]
- 아래는 이를 쉽게 풀이한 것이다:
- 현재 스택의 내용이 [math]\displaystyle{ s_i=a_it }[/math] 형토로 되어 있다면(즉, top에 [math]\displaystyle{ a_i }[/math]가 있다면)
- 입력 심볼 [math]\displaystyle{ w_{i+1} }[/math]를 읽고,
- PDA의 전이함수 [math]\displaystyle{ \delta }[/math]에 따라 [math]\displaystyle{ a_i }[/math]를 pop하고 [math]\displaystyle{ b_i }[/math]를 push하여 스택의 나머지 부분 t를 보존한다.
- 그 결과 PDA는 새로운 상태 [math]\displaystyle{ r_{i+1} }[/math]에 도달한다.
- 즉, DA가 스택의 맨 위를 조작하며 상태를 바꾸는 한 단계의 이동 규칙을 수학적으로 적은 것이다.
- [math]\displaystyle{ r_m \in F }[/math]: 마지막으로 PDA가 모든 입력을 처리한 후 accept 상태 집합 F에 속하는 상태에 도달해있다.
Computation Example
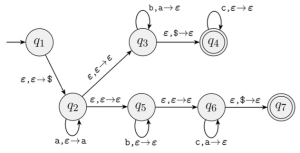
Figure 1은 아래 언어를 나타내는 언어의 구현을 나타낸 것이다:
[math]\displaystyle{ L = \{a^ib^jc^k|i,j,k \ge 0 \and (i = j \lor i = k)\} }[/math]
즉, a,b,c의 개수 관계가 i=j 또는 i=k인 문자열을 인식한다. 아래는 Figure 1에 나타난 PDA에 대한 설명이다:
- [math]\displaystyle{ q_1 \rightarrow q_2 }[/math]: 시작 시 스택에 기호 $ 삽입 (스택바닥표시).
- [math]\displaystyle{ q_2 }[/math]: a를 읽을 때마다 a를 push.
- [math]\displaystyle{ q_2 \rightarrow q_3 }[/math]: [math]\displaystyle{ \epsilon }[/math] 전이를 통해 “a와 b 개수를 비교하는 경로”로 진입
- [math]\displaystyle{ q_3 }[/math]: b를 읽을 때마다 a를 popg하여 i=j인 경우를 처리.
- [math]\displaystyle{ q_4 }[/math]: i=k이므로 수용 상태에 계속 머무른다.
- [math]\displaystyle{ q_5\sim q_7 }[/math]: 다른 경로 (nondeterminism)로 두 경우 모두 처리 가능하도록 설계.
PDA and CFG
PDA’s from CFG’s
모든 CFG는 어떤 PDA에 의해 인식되며, 이는 CFG→PDA 변환이 가능하다는 뜻이다. 이때 CFG를 PDA로 변환하는 것은 아래와 같이 스택을 이용하여 실현된다:
- 스택은 아직 남은 입력 문자열을 도출하기 위해 필요한 문장형식(sentential form)을 유지한다.
- CFG에서 문장을 생성할 때에는 "시작 비단말기 S"에서 여러 변환 규칙을 걸치면서 생성된다.
- PDA에서는 스택에 그 현재 문장형식(예: [math]\displaystyle{ S \rightarrow aSb \rightarrow aabb }[/math]) 의 “아직 처리되지 않은 부분”을 저장한다.[2]
- 스택의 top에 단말기가 있을 때, 그것이 현재 입력 문자열의 첫 글자와 비교한다.
- 두 문자가 같다면 스택에서 pop하고 입력에서도 consume한다.
- 같지 않다면 PDA의 그 “계산 경로(computation path)”는 실패한다.
- 만약 스택의 top이 비단말기라면, CFG의 생성 규칙 중 하나를 비결정적(nondeterministically) 선택한다.
- 만약 선택된 생성 규칙이 [math]\displaystyle{ A \rightarrow aBb }[/math]라면, 스택의 top인 [math]\displaystyle{ A }[/math]를 pop하고, [math]\displaystyle{ b,B,a }[/math]를 역순으로 push한다.
- 스택의 내용이 다 처리되어 비면[3] PDA는 accept state 로 이동한다.[4]
PDA's states
CFG에서 만든 PDA는 아래와 같은 세 가지 핵심적인 상태를 가진다:
- [math]\displaystyle{ q_{start} }[/math]: 시작 상태
- 스택에 [math]\displaystyle{ $S }[/math]를 push한다.[5]
- 다음 상태는 [math]\displaystyle{ q_{loop} }[/math]이다.
- [math]\displaystyle{ q_{loop} }[/math]: 반복 상태
- 스택의 top이 단말기면 입력과 비교하여 “match” 후 pop한다.
- 스택의 top이 비단말기면 CFG의 생성 규칙 중 하나를 비결정적으로 선택하여 스택을 확장한다.
- 스택의 top이 $이면 [math]\displaystyle{ q_{accept} }[/math]로 이동
- [math]\displaystyle{ q_{accept} }[/math]: Accept 상태
- 스택이 완전히 비고 입력이 끝난 상태이다.
이때 만약 여러 symbol을 한꺼번에 push해야 할 때는, “extra states”를 임시로 만들어 연속 push를 구현한다.
PDA from CFG Example
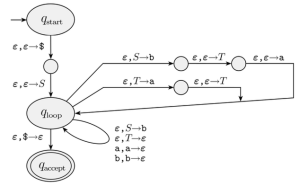
아래와 같은 CFG가 주어졌다고 가정해보자:
[math]\displaystyle{ S \rightarrow aTb | b }[/math] [math]\displaystyle{ T \rightarrow Ta|\epsilon }[/math]
이를 구현하기 위해서는 [math]\displaystyle{ q_{start}, q_{loop}, q_{accept} }[/math]를 구현해야 하며, 스택을 CFG 규칙에 맞추어 조작해야 한다. 이는 figure 2를 관찰하면 어떻게 구현이 되었는지 잘 이해할 수 있다.
CFG’s from PDA’s
모든 PDA는 어떤 CFG를 생성하는데, 이는 PDA→CFG 변환이 가능하다는 뜻이다. 이를 CFG의 비단말기는 [math]\displaystyle{ A_{pq} }[/math] 형태로 만든다.[6] 이때 아래의 식이 성립한다:
[math]\displaystyle{ A_{pq} \Rightarrow* w \Leftrightarrow }[/math]PDA가 입력되는 w를 읽으면서 상태 p에서 q로 이동하고, 스택이 완전히 비워짐
즉, CFG의 규칙은 PDA의 이동경로를 기반으로 구성된다. 또한 아래는 CFG를 만들기 위한 PDA 단순화 전제이다:
- PDA P는 정확히 하나의 Accept 상태 [math]\displaystyle{ q_{accept} }[/math] 만을 가진다.
- Accept 상태에 도달하기 위해서는 스택이 완전히 비워져야 한다.
- 각 전이함수는 push 하나 또는 pop 하나만 수행한다.
Definition of G
위의 내용을 사용하여 CFG를 구체적으로 아래와 같이 정의한다:
- 변수 집합: [math]\displaystyle{ V = \{A_{pq}|p,q \in Q\} }[/math]
- 시작 변수: [math]\displaystyle{ S = A_{q_0q_{accept}} }[/math][9]
- 생성 규칙: “u를 스택에 넣고 다시 꺼내는 과정 사이에 있는 계산 전체”를 문법 규칙 하나로 표현한다:
이러한 규칙을 통해 CFG가 PDA의 “스택 조작 기반 계산 경로”를 그대로 재현할 수 있다.
CFG from PDA Example
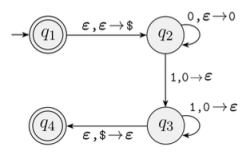
Figure 3에서 CFG는 아래와 같이 유도된다:
[math]\displaystyle{ A_{14}\rightarrow A_{23} }[/math] ($를 push한 후, $를 pop) [math]\displaystyle{ A_{23}\rightarrow 0A_{23}1 }[/math] (0을 push한 후, 0을 pop) [math]\displaystyle{ A_{23}\rightarrow 0A_{22}1 }[/math] (0을 push한 후, 0을 pop) [math]\displaystyle{ A_{22}\rightarrow \epsilon }[/math]
위에서 [math]\displaystyle{ A_{14} }[/math]는 PDA의 시작 상태 [math]\displaystyle{ q_1 }[/math]에서 accept 상태 [math]\displaystyle{ q_4 }[/math]까지 가는 모든 입력 문자열을 생성하는 비단말기이다. 따라서 해당 비단말기는 주어진 PDA가 인식하는 언어 전체를 생성해야 하므로 [math]\displaystyle{ S=A_{14} }[/math]가 PDA로부터 정의되는 문법의 시작 기호 역할을 한다.
[math]\displaystyle{ A_{14}\rightarrow A_{23} }[/math]과 같은 규칙은 아래의 두 전이:
[math]\displaystyle{ (q_1,\epsilon,\epsilon)\rightarrow (q_2,$) }[/math] [math]\displaystyle{ (q_3,\epsilon,$)\rightarrow (q_4,\epsilon) }[/math]
을 $에 대한 push와 pop의 짝으로 연결한 것이다. 첫 단계에서는 스택에 $를 push하며, 마지막 단계에서는 $를 스택에서 pop한다. 이에 따라 [math]\displaystyle{ A_{23} }[/math]는 두 단계 사이의 계산, 즉 PDA의 [math]\displaystyle{ q_2 }[/math]에서 [math]\displaystyle{ q_3 }[/math]까지의 계산을 의미하는 비단말기이다. 즉, [math]\displaystyle{ A_{14}\rightarrow A_{23} }[/math] 규칙은 [math]\displaystyle{ q_1 }[/math]에서 $를 push하는 것으로 시작해 [math]\displaystyle{ q_4 }[/math]에서 $를 pop하며 끝나는 전체 계산은 [math]\displaystyle{ q_2 }[/math]에서 [math]\displaystyle{ q_3 }[/math] 사이에서의 계산과 같다는 것을 의미한다.
[math]\displaystyle{ A_{23}\rightarrow 0A_{23}1 }[/math]과 같은 규칙은 아래의 두 전이:
[math]\displaystyle{ (q_2,0,\epsilon)\rightarrow (q_2,0) }[/math] [math]\displaystyle{ (q_3,1,0)\rightarrow (q_3,\epsilon) }[/math]
을 0에 대한 push와 pop의 짝으로 연결한 것이다. 또한 [math]\displaystyle{ A_{23}\rightarrow 0A_{22}1 }[/math]과 같은 규칙은 아래의 두 전이:
[math]\displaystyle{ (q_2,0,\epsilon)\rightarrow (q_2,0) }[/math] [math]\displaystyle{ (q_2,1,0)\rightarrow (q_3,\epsilon) }[/math]
을 0에 대한 push와 pop의 짝으로 연결한 것이다. 이때 다른 두 비단말기에 비해 이질적인 [math]\displaystyle{ A_{22} }[/math]은 그 정의에 따르면 PDA가 [math]\displaystyle{ q_2 }[/math]에서 시작해서 다시 [math]\displaystyle{ q_2 }[/math]로 돌아오는 과정에서 스택의 상태가 처음과 같게 유지되는 모든 문자열들의 집합을 표현하는 비단말기이다. 이에 따라 스택이 유지되기 위해서는 push와 pop의 수가 같아야 하므로, [math]\displaystyle{ A_{33} }[/math]에서 유도될 수 있는 문자열은 [math]\displaystyle{ \epsilon }[/math] 뿐이다.
각주
- ↑ 해당 문서에서는 특별한 언급이 없는 이상 nondeterministic PDA를 기본으로 하여 서술한다.
- ↑ 즉, 스택은 “현재 어디까지 유도했는지”를 나타낸다.
- ↑ 스택의 top이 $기호인 경우이다.
- ↑ 이는 모든 입력이 정확히 문법으로부터 생성될 수 있다는 뜻이다.
- ↑ [math]\displaystyle{ S }[/math]는 시작 비단말이고, $는 스택의 바닥을 표시한다.
- ↑ p, q는 PDA의 상태 집합의 원소이다.
- ↑ 쉽게 말하면, “상태 p에서 시작해서 q로 갈 수 있는 입력 문자열”을 대표하는 문법 기호이다.
- ↑ 다르게 설명하면, 상태 p에서 상태 q로 이동하는 과정에서 스택의 상태가 처음과 같게 유지되는 모든 문자열들의 집합을 의미한다.
- ↑ PDA의 시작 상태 [math]\displaystyle{ q_0 }[/math]에서 accept 상태까지 가는 문자열을 생성해야 하므로, 문법의 시작기호는 이렇게 설정됩니다.
- ↑ p에서 q로 가는 계산은 a를 읽고 u를 푸시한 뒤, 중간에 r에서 s로 이동하면서 u를 팝하며 b를 읽는다는 것을 나타낸다.
- ↑ 같은 상태에서 아무 동작 없이 스택이 빈 경우이다.
