다른 명령
새 문서: 분류:알고리즘 설계와 분석 분류:컴퓨터 공학 상위 문서: 알고리즘 설계와 분석 ==개요== 그래프는 알고리즘, 네트워크, 데이터 구조 등 컴퓨터 과학의 여러 분야에서 핵심적인 개념이다. 그래프의 정의를 수학적으로 표현하면 아래와 같다: A graph <math>G=(V,E)</math> is defined by a set of vertices <math>V</math>, and a set of edges <math>E</math> consis... |
잔글 봇: 자동으로 텍스트 교체 (-\[\[분류:컴퓨터 공학(\|[^\]]+)?\]\] +) |
||
| (다른 사용자 한 명의 중간 판 12개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
[[분류:알고리즘 설계와 분석]] | [[분류:알고리즘 설계와 분석]] | ||
상위 문서: [[알고리즘 설계와 분석#Graph|알고리즘 설계와 분석]] | 상위 문서: [[알고리즘 설계와 분석#Graph|알고리즘 설계와 분석]] | ||
==개요== | ==개요== | ||
[[파일:Figure 1. Directed Graph.png|섬네일|200x200픽셀|Figure 1. Directed Graph]] | |||
그래프는 알고리즘, 네트워크, 데이터 구조 등 컴퓨터 과학의 여러 분야에서 핵심적인 개념이다. 그래프의 정의를 수학적으로 표현하면 아래와 같다: | 그래프는 알고리즘, 네트워크, 데이터 구조 등 컴퓨터 과학의 여러 분야에서 핵심적인 개념이다. 그래프의 정의를 수학적으로 표현하면 아래와 같다: | ||
A graph <math>G=(V,E)</math> is defined by a set of vertices <math>V</math>, and a set of edges <math>E</math> consisting of ordered or unordered pairs of vertices from <math>V</math>. | A graph <math>G=(V,E)</math> is defined by a set of vertices <math>V</math>, and a set of edges <math>E</math> consisting of ordered or unordered pairs of vertices from <math>V</math>. | ||
| 9번째 줄: | 10번째 줄: | ||
* <math>V</math>: 그래프를 구성하는 정점들의 집합 (Vertices set) | * <math>V</math>: 그래프를 구성하는 정점들의 집합 (Vertices set) | ||
* <math>E</math>: 정점들을 잇는 간선들의 집합 (Edges set) | * <math>E</math>: 정점들을 잇는 간선들의 집합 (Edges set) | ||
이때 간선들의 집합 E는 <math>E=\{(u,v),(x,y)\}</math>와 같이 정점의 쌍(pair)로 이루어진 원소들의 집합이며, 각 간선 <math>(A, B)</math>는 정점 A에서 정점 B 방향으로 연결되어 있음을 의미한다. | 이때 간선들의 집합 E는 <math>E=\{(u,v),(x,y)\}</math>와 같이 정점의 쌍(pair)로 이루어진 원소들의 집합이며, 각 간선 <math>(A, B)</math>는 정점 A에서 정점 B 방향으로 연결되어 있음을 의미한다. | ||
어떤 정점의 degree는 그 정점에 연결된 간선(친구 관계)의 수를 의미한다. 또한 clique란 모든 정점 쌍이 직접 연결되어 있는 부분을 의미한다. 이는 경로가 존재하기만 하면 되는 connected 개념과는 대비된다. 예를 들어 아래와 같은 예시를 보자: | |||
A-B-C-D | |||
이 그래프는 A–B–C–D로 이어진 path이므로 전체적으로는 connected이다. 그러나 모든 정점 쌍이 직접 연결되어 있지 않기 때문에 전체가 clique가 될 수 없다. 이 그래프에서 가능한 clique는 “크기가 2인 clique”들뿐이며, 그것들은 {A, B}, {B, C}, {C, D}과 같이 총 3개가 존재한다. | |||
이러한 그래프의 개념은 사회적 네트워크, 전자 회로, 도로망, 프로그램 컨트롤 플로우 등 다양한 분야에 적용될 수 있다. | 이러한 그래프의 개념은 사회적 네트워크, 전자 회로, 도로망, 프로그램 컨트롤 플로우 등 다양한 분야에 적용될 수 있다. | ||
| 22번째 줄: | 27번째 줄: | ||
===Weighted vs. Unweighted Graphs=== | ===Weighted vs. Unweighted Graphs=== | ||
가중치(Weighted) 그래프는 각 간선(혹은 정점)에 가중치(weight)를 부여하는 그래프이다. 가중치는 거리, 비용, 시간, 용량 등 수량적인 값이다. Figure | [[파일:Figure 2. Weighted Graph.png|섬네일|200x200픽셀|Figure 2. Weighted Graph]] | ||
가중치(Weighted) 그래프는 각 간선(혹은 정점)에 가중치(weight)를 부여하는 그래프이다. 가중치는 거리, 비용, 시간, 용량 등 수량적인 값이다. Figure 2의 경우, 각 간선마다 있는 숫자들은 각 경로의 “비용”을 나타낸다. 이는 실제 도로 등에서 거리, 운전 시간, 정체 등을 나타내는 데 사용된다. 또한 가중치가 있으면 Dijkstra, Bellman-Ford 등의 알고리즘을 사용할 수 있다. | |||
반면 가중치가 있지 않은 그래프를 비가중치 그래프(unweighted)라고 하며, 해당 그래프에서는 모든 간선이 동일한 ‘비용’을 가지므로 단순히 “연결 여부”만 중요하다. 이런 그래프에서는 BFS 알고리즘 등을 활용할 수 있다. | 반면 가중치가 있지 않은 그래프를 비가중치 그래프(unweighted)라고 하며, 해당 그래프에서는 모든 간선이 동일한 ‘비용’을 가지므로 단순히 “연결 여부”만 중요하다. 이런 그래프에서는 BFS 알고리즘 등을 활용할 수 있다. | ||
===Simple vs. Non-simple Graphs=== | ===Simple vs. Non-simple Graphs=== | ||
간선에는 self-loop와 multi-edge와 같은 특수한 간선들이 존재한다. Self-loop란 <math>(A,A)</math>와 같이 자기 자신으로 향하는 간선을 의미한다. 또한 multi-edge란 동일한 정점 쌍 사이에 여러 간선들이 존재하는 것을 의미한다. Figure | [[파일:Figure 3. Non-simple Graph.png|섬네일|200x200픽셀|Figure 3. Non-simple Graph]] | ||
간선에는 self-loop와 multi-edge와 같은 특수한 간선들이 존재한다. Self-loop란 <math>(A,A)</math>와 같이 자기 자신으로 향하는 간선을 의미한다. 또한 multi-edge란 동일한 정점 쌍 사이에 여러 간선들이 존재하는 것을 의미한다. Figure 3에서 자기 자신으로 연결된 붉은 고리는 self-loop에 해당하고, 두 정점 사이의 여러 선은 multi-edge에 해당한다. | |||
이때 simple 그래프란 self-loop와 multi-edge가 없는 그래프이다. 반면 Non-simple 그래프란 둘 중 하나라도 포함하는 그래프를 의미한다. | 이때 simple 그래프란 self-loop와 multi-edge가 없는 그래프이다. 반면 Non-simple 그래프란 둘 중 하나라도 포함하는 그래프를 의미한다. | ||
| 35번째 줄: | 42번째 줄: | ||
===Cyclic vs. Acyclic Graphs=== | ===Cyclic vs. Acyclic Graphs=== | ||
그래프에서 사이클(cycle)이란, 같은 정점으로 되돌아오는 경로가 존재하는 경우를 의미한다. 이때 사이클이 존재하는 그래프는 cyclic 그래프라고 하며, 반면 사이클이 존재하지 않는 그래프는 acyclic 그래프라고 한다. 예를 들어 트리(Tree) 자료구조는 connected acyclic undirected 그래프이다. 또한 Figure | [[파일:Figure 4. Acyclic Graph.png|섬네일|200x200픽셀|Figure 4. Acyclic Graph]] | ||
그래프에서 사이클(cycle)이란, 같은 정점으로 되돌아오는 경로가 존재하는 경우를 의미한다. 이때 사이클이 존재하는 그래프는 cyclic 그래프라고 하며, 반면 사이클이 존재하지 않는 그래프는 acyclic 그래프라고 한다. 예를 들어 트리(Tree) 자료구조는 connected acyclic undirected 그래프이다. 또한 Figure 4는 directed acyclic 그래프인데, 이러한 그래프를 DAG라고 한다. | |||
===Embedded vs. Topological Graphs=== | ===Embedded vs. Topological Graphs=== | ||
Topological 그래프는 그래프의 모양보다는 연결 구조만 중요한 그래프이다. 즉, 간선이 교차하든 구부러지든 관계없고, 단지 정점 사이의 연결 관계만을 따지는 그래프이다. 반면, embedded 그래프는 그래프의 “그림” 또는 “좌표 위치”가 중요한 그래프이다. 이에 따라 도로망, 회로망, 지리적 네트워크처럼 실제 공간에 배치되는 경우에 사용된다. | Topological 그래프는 그래프의 모양보다는 연결 구조만 중요한 그래프이다. 즉, 간선이 교차하든 구부러지든 관계없고, 단지 정점 사이의 연결 관계만을 따지는 그래프이다. 반면, embedded 그래프는 그래프의 “그림” 또는 “좌표 위치”가 중요한 그래프이다. 이에 따라 도로망, 회로망, 지리적 네트워크처럼 실제 공간에 배치되는 경우에 사용된다. | ||
===Connected/Strongly Connected Graphs=== | |||
그래프의 어떤 두 정점 사이에도 경로(path)가 존재한다면 그 그래프는 연결되어 있다고 한다. 이때 "connected"라는 말은 "간선 방향을 무시하면(undirected로 바꾸면) 연결되어 있다"는 것을 뜻한다. 따라서 화살표 방향은 신경 안 쓰고, 단순히 서로 닿을 수만 있으면 connected라고 할 수 있다. | |||
Directed 그래프에 대해서는 모든 정점 쌍 u,v에 대해 u→v, v→u 두 방향 경로가 모두 존재하는 경우 이를 strongly connected 그래프라고 한다. 이때 정의에 의해서 strongly connected 그래프는 반드시 cycle을 포함한다. | |||
==Data Structures for Graphs== | ==Data Structures for Graphs== | ||
| 58번째 줄: | 71번째 줄: | ||
|리스트 | |리스트 | ||
|- | |- | ||
| | |sparse 그래프에서의 메모리 사용 | ||
|리스트 (m+n vs n<sup>2</sup>) | |리스트 (m+n vs n<sup>2</sup>) | ||
|- | |- | ||
| | |dense 그래프에서의 메모리 사용 | ||
|행렬 | |행렬 | ||
|- | |- | ||
| 82번째 줄: | 95번째 줄: | ||
struct edgenode *next; // 다음 간선으로의 포인터 (연결 리스트) | struct edgenode *next; // 다음 간선으로의 포인터 (연결 리스트) | ||
} edgenode; | } edgenode; | ||
< /syntaxhighlight> | </syntaxhighlight> | ||
즉, 한 정점에 연결된 간선들을 연결 리스트 형태로 연결시켜서 표현한다. 아래는 그래프 전체를 담는 구조체이다: | 즉, 한 정점에 연결된 간선들을 연결 리스트 형태로 연결시켜서 표현한다. 아래는 그래프 전체를 담는 구조체이다: | ||
<syntaxhighlight lang="c"> | <syntaxhighlight lang="c"> | ||
| 92번째 줄: | 105번째 줄: | ||
int directed; // 방향 그래프 여부 | int directed; // 방향 그래프 여부 | ||
} graph; | } graph; | ||
< /syntaxhighlight> | </syntaxhighlight> | ||
degree[i] 는 정점 i의 차수를 나타낸다. 또한 무방향 그래프에서는 간선 (x, y)를 저장할 때 두 번 저장하는데, 한 번은 x의 리스트에 y로, 다른 한 번은 y의 리스트에 x로 추가한다. 아래는 그래프의 정점 수와 간선 수를 0으로 초기화하는 함수이다: | degree[i] 는 정점 i의 차수를 나타낸다. 또한 무방향 그래프에서는 간선 (x, y)를 저장할 때 두 번 저장하는데, 한 번은 x의 리스트에 y로, 다른 한 번은 y의 리스트에 x로 추가한다. 아래는 그래프의 정점 수와 간선 수를 0으로 초기화하는 함수이다: | ||
<syntaxhighlight lang="c"> | <syntaxhighlight lang="c"> | ||
| 103번째 줄: | 116번째 줄: | ||
for (i = 1; i <= MAXV; i++) g->edges[i] = NULL; // 모든 차수 배열과 포인터를 초기화 | for (i = 1; i <= MAXV; i++) g->edges[i] = NULL; // 모든 차수 배열과 포인터를 초기화 | ||
} | } | ||
< /syntaxhighlight> | </syntaxhighlight> | ||
아래는 파일이나 입력으로부터 그래프를 읽어들이고, 이를 그래프에 반영하는 과정이다. | 아래는 파일이나 입력으로부터 그래프를 읽어들이고, 이를 그래프에 반영하는 과정이다. | ||
<syntaxhighlight lang="c"> | <syntaxhighlight lang="c"> | ||
| 115번째 줄: | 128번째 줄: | ||
} | } | ||
} | } | ||
< /syntaxhighlight> | </syntaxhighlight> | ||
아래는 그래프에 간선을 추가하는 함수이다: | 아래는 그래프에 간선을 추가하는 함수이다: | ||
<syntaxhighlight lang="c"> | <syntaxhighlight lang="c"> | ||
| 131번째 줄: | 144번째 줄: | ||
g->nedges++; | g->nedges++; | ||
} | } | ||
< /syntaxhighlight> | </syntaxhighlight> | ||
==Graph Traversal== | |||
그래프 탐색(Graph Traversal)은 그래프에 있는 모든 정점과 간선을 체계적으로 방문하는 과정을 의미한다. 이를 위해 쓰이는 주요한 알고리즘은 [[DFS|DFS(Depth-First Search, 깊이 우선 탐색)]]와 [[BFS|BFS(Breadth-First Search, 너비 우선 탐색)]]이다. | |||
[[BFS]]에 대한 자세한 내용은 해당 문서를 참조하십시오.<br> | |||
[[DFS]]에 대한 자세한 내용은 해당 문서를 참조하십시오. | |||
그래프 탐색에서 중요한 것은 효율성(Efficiency)과 정확성(Correctness)이다. 먼저 효율성이란 각 간선(edge)을 최대 한 번 또는 두 번까지만 방문해야 한다는 것이다. 만약 방문을 여러 번 반복하면 시간 낭비가 생기고, 알고리즘이 비효율적이다. 또한 정확성이란 체계적(systematic) 으로 탐색을 하여 “방문하지 않은 정점이 남지 않게” 하는 것이다. 이를 위해서 미로 탐색(maze)과 마찬가지로, 한 번 간 길은 표시해두고, 어디까지 갔는지 기록해야 한다. | |||
이때 정점의 상태를 표시(marking) 하는 것은 그래프 탐색에서 가장 중요한 개념 중 하나이다. 각 정점은 아래와 같아 항상 세 가지 상태 중 하나의 상태에 있다: | |||
* undiscovered: 탐색이 시작되기 전, 아직 전혀 방문하지 않은 상태. | |||
* discovered: 방문은 했지만, 그 정점에서 나가는 간선들을 아직 모두 확인하지 않은 상태. | |||
* processed: 해당 정점의 모든 간선을 다 검사한 후 완전히 끝낸 상태. | |||
이때, 그래프 탐색 과정에서 모든 정점은 undiscovered → discovered → processed 순서로 상태가 바뀐다. 이에 따라 DFS나 BFS 알고리즘에서는 이 상태를 배열로 관리한다. 따라서 발견했지만 아직 처리가 끝나지 않은 정점들을 저장하는 자료구조가 필요하며, BFS에서는 큐(Queue)를 , DFS에서는 스택(Stack)을 활용한다. | |||
기본적인 탐색알고리즘의 절차는 아래와 같다: | |||
# 처음엔 시작 정점 하나만 discovered 상태이며, 해당 정점을 꺼내서 모든 인접 정점을 확인한다. | |||
# 새로 발견된 정점은 “discovered” 로 바꾸고 to-do list(큐/스택) 에 넣는다. | |||
# 해당 정점의 모든 간선을 검사한 뒤에는 “processed” 상태로 바꾼다. | |||
# to-do list 가 빌 때까지 계속 반복한다. | |||
==[[Minimum Spanning Trees]]== | |||
자세한 내용은 [[Minimum Spanning Trees]] 문서를 참조하십시오. | |||
==각주== | ==각주== | ||
2026년 1월 15일 (목) 15:21 기준 최신판
상위 문서: 알고리즘 설계와 분석
개요
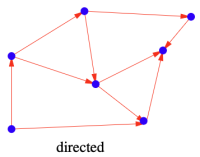
그래프는 알고리즘, 네트워크, 데이터 구조 등 컴퓨터 과학의 여러 분야에서 핵심적인 개념이다. 그래프의 정의를 수학적으로 표현하면 아래와 같다:
A graph [math]\displaystyle{ G=(V,E) }[/math] is defined by a set of vertices [math]\displaystyle{ V }[/math], and a set of edges [math]\displaystyle{ E }[/math] consisting of ordered or unordered pairs of vertices from [math]\displaystyle{ V }[/math].
이를 조금 더 간단히 풀면, 그래프(Graph) 는 정점(Vertex) 과 간선(Edge) 으로 이루어진 집합이라는 것이다. 그래프 표기 [math]\displaystyle{ G=(V,E) }[/math]는
- [math]\displaystyle{ V }[/math]: 그래프를 구성하는 정점들의 집합 (Vertices set)
- [math]\displaystyle{ E }[/math]: 정점들을 잇는 간선들의 집합 (Edges set)
이때 간선들의 집합 E는 [math]\displaystyle{ E=\{(u,v),(x,y)\} }[/math]와 같이 정점의 쌍(pair)로 이루어진 원소들의 집합이며, 각 간선 [math]\displaystyle{ (A, B) }[/math]는 정점 A에서 정점 B 방향으로 연결되어 있음을 의미한다.
어떤 정점의 degree는 그 정점에 연결된 간선(친구 관계)의 수를 의미한다. 또한 clique란 모든 정점 쌍이 직접 연결되어 있는 부분을 의미한다. 이는 경로가 존재하기만 하면 되는 connected 개념과는 대비된다. 예를 들어 아래와 같은 예시를 보자:
A-B-C-D
이 그래프는 A–B–C–D로 이어진 path이므로 전체적으로는 connected이다. 그러나 모든 정점 쌍이 직접 연결되어 있지 않기 때문에 전체가 clique가 될 수 없다. 이 그래프에서 가능한 clique는 “크기가 2인 clique”들뿐이며, 그것들은 {A, B}, {B, C}, {C, D}과 같이 총 3개가 존재한다.
이러한 그래프의 개념은 사회적 네트워크, 전자 회로, 도로망, 프로그램 컨트롤 플로우 등 다양한 분야에 적용될 수 있다.
Flavors of Graphs
그래프는 단순히 ordered/unordered로 나뉘지 않고, 다양한 종류(flavor)로 나뉜다. 즉, 그래프는 단순히 정점과 간선으로만 정의되는 것이 아니라, 방향성·가중치·구조·밀도·위상적 특성 등에 따라 여러 종류로 나뉜다.
Directed vs. Undirected Graphs
Undirected 그래프의 정의는 아래와 같다:
A graph [math]\displaystyle{ G=(V,E) }[/math] is undirected if edge [math]\displaystyle{ (x, y) \in E \rightarrow (y, x) \in E }[/math].
즉, 이는 만약 (x, y)가 간선 집합에 포함되어 있을때 (y, x)도 자동으로 포함된다면, 해당 그래프 G는 undirected라는 뜻이다. 이때 undirected 그래프의 간선은 unordered pair이며, 해당 간선은 양방향으로 연결되어 있다. 반대로 undirected 그래프가 아닌 그래프는 directed이다. 또한 directed 그래프의 간선은 ordered pair이며, 해당 간선은 일방적으로 연결되어 있다.
Weighted vs. Unweighted Graphs
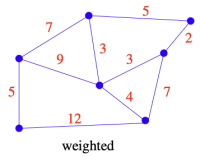
가중치(Weighted) 그래프는 각 간선(혹은 정점)에 가중치(weight)를 부여하는 그래프이다. 가중치는 거리, 비용, 시간, 용량 등 수량적인 값이다. Figure 2의 경우, 각 간선마다 있는 숫자들은 각 경로의 “비용”을 나타낸다. 이는 실제 도로 등에서 거리, 운전 시간, 정체 등을 나타내는 데 사용된다. 또한 가중치가 있으면 Dijkstra, Bellman-Ford 등의 알고리즘을 사용할 수 있다.
반면 가중치가 있지 않은 그래프를 비가중치 그래프(unweighted)라고 하며, 해당 그래프에서는 모든 간선이 동일한 ‘비용’을 가지므로 단순히 “연결 여부”만 중요하다. 이런 그래프에서는 BFS 알고리즘 등을 활용할 수 있다.
Simple vs. Non-simple Graphs
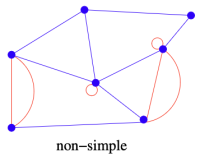
간선에는 self-loop와 multi-edge와 같은 특수한 간선들이 존재한다. Self-loop란 [math]\displaystyle{ (A,A) }[/math]와 같이 자기 자신으로 향하는 간선을 의미한다. 또한 multi-edge란 동일한 정점 쌍 사이에 여러 간선들이 존재하는 것을 의미한다. Figure 3에서 자기 자신으로 연결된 붉은 고리는 self-loop에 해당하고, 두 정점 사이의 여러 선은 multi-edge에 해당한다.
이때 simple 그래프란 self-loop와 multi-edge가 없는 그래프이다. 반면 Non-simple 그래프란 둘 중 하나라도 포함하는 그래프를 의미한다.
Sparse vs. Dense Graphs
Sparse 그래프란 가능한 모든 정점 쌍 중 실제로 연결된 간선의 수가 적은 그래프를 의미한다. 반대로 대부분의 정점쌍이 연결되어 있는 경우는 dense 그래프라고 한다. 수학적으로는 정점의 개수가 n개일 때 sparse 그래프의 간선의 수는 O(n)에 비례하며, dense 그래프의 간선의 수는 O(n2)에 비례한다.
Cyclic vs. Acyclic Graphs
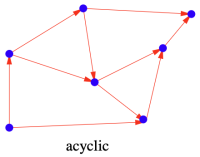
그래프에서 사이클(cycle)이란, 같은 정점으로 되돌아오는 경로가 존재하는 경우를 의미한다. 이때 사이클이 존재하는 그래프는 cyclic 그래프라고 하며, 반면 사이클이 존재하지 않는 그래프는 acyclic 그래프라고 한다. 예를 들어 트리(Tree) 자료구조는 connected acyclic undirected 그래프이다. 또한 Figure 4는 directed acyclic 그래프인데, 이러한 그래프를 DAG라고 한다.
Embedded vs. Topological Graphs
Topological 그래프는 그래프의 모양보다는 연결 구조만 중요한 그래프이다. 즉, 간선이 교차하든 구부러지든 관계없고, 단지 정점 사이의 연결 관계만을 따지는 그래프이다. 반면, embedded 그래프는 그래프의 “그림” 또는 “좌표 위치”가 중요한 그래프이다. 이에 따라 도로망, 회로망, 지리적 네트워크처럼 실제 공간에 배치되는 경우에 사용된다.
Connected/Strongly Connected Graphs
그래프의 어떤 두 정점 사이에도 경로(path)가 존재한다면 그 그래프는 연결되어 있다고 한다. 이때 "connected"라는 말은 "간선 방향을 무시하면(undirected로 바꾸면) 연결되어 있다"는 것을 뜻한다. 따라서 화살표 방향은 신경 안 쓰고, 단순히 서로 닿을 수만 있으면 connected라고 할 수 있다.
Directed 그래프에 대해서는 모든 정점 쌍 u,v에 대해 u→v, v→u 두 방향 경로가 모두 존재하는 경우 이를 strongly connected 그래프라고 한다. 이때 정의에 의해서 strongly connected 그래프는 반드시 cycle을 포함한다.
Data Structures for Graphs
그래프 [math]\displaystyle{ G=(V, E) }[/math]는 정점(vertex) 집합 V 과 간선(edge) 집합 E 으로 구성된다. 이때 정점의 개수를 n, 간선의 개수를 m 이라고 하면, 이를 단순하게 n2 크기의 2차월 배열 M으로 정의할 수 있다. 이때:
- M[i][j]=1 이면 정점 i 에서 j 로의 간선이 존재함을 의미하고,
- M[i][j]=0 이면 간선이 없다는 뜻이다.
이러한 방식을 인접 행렬(adjacency matrix)이라고 한다. 이는 간단하고 직관적이지만, 간선이 매우 적은 sparse 그래프(sparse graph)의 경우에도 n2 크기를 모두 차지해야 한다는 단점이 있다. 즉, 공간 낭비가 크다는 단점이 있다.
위와 같은 문제를 해결하기 위한 방식이 인접 리스트(adjacency list)이다. 이는 각 정점마다 “해당 정점과 연결된 정점들”을 연결 리스트(linked list) 형태로 저장한다. 각 i 번째 정점은 배열의 i 번째 원소에 저장되며, 배열의 각 원소는 해당하는 정점의 인접한 정점들을 담고 있는 리스트의 포인터이다. 예를 들어, 정점 1이 2, 5와 연결되어 있다면 edges[1] → 2 → 5 → NULL 형태가 된다. 따라서 sparse 그래프에서는 연결 수가 적기 때문에 메모리를 훨씬 적게 사용한다는 장점이 있다. 또한, 어떤 정점에 연결되어 있는 정점을 모두 탐색하고 경우, 시간 복잡도는 O(di[1])로, O(n)보다 훨씬 작을 수 있다. 하지만 특정한 간선 (i,j) 의 존재 여부를 확인하려면 리스트를 순회해야 하므로, 인접 행렬보다는 느리다는 단점이 있다.
| 비교 항목 | 더 좋은 쪽 |
|---|---|
| 간선 존재 여부 확인 | 행렬 (O(1)) |
| 정점의 차수(degree) 구하기 | 리스트 |
| sparse 그래프에서의 메모리 사용 | 리스트 (m+n vs n2) |
| dense 그래프에서의 메모리 사용 | 행렬 |
| 간선 삽입/삭제 속도 | 행렬 (O(1)) |
| 그래프 전체 순회 속도 | 리스트 (m+n vs n2) |
| 대부분의 문제에서 유리한 구조 | 리스트 |
Implementing Adjancency Lists
아래는 인접 리스트에 저장되는 간선의 구조체 정의이다:
typedef struct edgenode {
int y; // 간선이 연결된 상대 정점
int weight; // 가중치 (weighted graph일 경우)
struct edgenode *next; // 다음 간선으로의 포인터 (연결 리스트)
} edgenode;
즉, 한 정점에 연결된 간선들을 연결 리스트 형태로 연결시켜서 표현한다. 아래는 그래프 전체를 담는 구조체이다:
typedef struct {
edgenode *edges[MAXV+1]; // 각 정점의 인접 리스트 시작 포인터
int degree[MAXV+1]; // 각 정점의 차수
int nvertices; // 정점 개수
int nedges; // 간선 개수
int directed; // 방향 그래프 여부
} graph;
degree[i] 는 정점 i의 차수를 나타낸다. 또한 무방향 그래프에서는 간선 (x, y)를 저장할 때 두 번 저장하는데, 한 번은 x의 리스트에 y로, 다른 한 번은 y의 리스트에 x로 추가한다. 아래는 그래프의 정점 수와 간선 수를 0으로 초기화하는 함수이다:
void initialize_graph(graph *g, bool directed) {
int i;
g->nvertices = 0;
g->nedges = 0;
g->directed = directed; // 방향성 여부를 저장
for (i = 1; i <= MAXV; i++) g->degree[i] = 0;
for (i = 1; i <= MAXV; i++) g->edges[i] = NULL; // 모든 차수 배열과 포인터를 초기화
}
아래는 파일이나 입력으로부터 그래프를 읽어들이고, 이를 그래프에 반영하는 과정이다.
void read_graph(graph *g, bool directed) {
int i, m, x, y;
initialize_graph(g, directed);
scanf("%d %d", &(g->nvertices), &m); // 정점과 간선 개수 읽기
for (i = 1; i <= m; i++) {
scanf("%d %d", &x, &y); // 간선 정보 읽기
insert_edge(g, x, y, directed); // 간선 삽입
}
}
아래는 그래프에 간선을 추가하는 함수이다:
void insert_edge(graph *g, int x, int y, bool directed) {
edgenode *p;
p = malloc(sizeof(edgenode)); // 새 간선 노드 생성
p->weight = 0;
p->y = y;
p->next = g->edges[x]; // 리스트의 맨 앞에 삽입
g->edges[x] = p;
g->degree[x]++;
if (!directed)
insert_edge(g, y, x, true); // 무방향이면 반대 방향도 추가
else
g->nedges++;
}
Graph Traversal
그래프 탐색(Graph Traversal)은 그래프에 있는 모든 정점과 간선을 체계적으로 방문하는 과정을 의미한다. 이를 위해 쓰이는 주요한 알고리즘은 DFS(Depth-First Search, 깊이 우선 탐색)와 BFS(Breadth-First Search, 너비 우선 탐색)이다.
BFS에 대한 자세한 내용은 해당 문서를 참조하십시오.
DFS에 대한 자세한 내용은 해당 문서를 참조하십시오.
그래프 탐색에서 중요한 것은 효율성(Efficiency)과 정확성(Correctness)이다. 먼저 효율성이란 각 간선(edge)을 최대 한 번 또는 두 번까지만 방문해야 한다는 것이다. 만약 방문을 여러 번 반복하면 시간 낭비가 생기고, 알고리즘이 비효율적이다. 또한 정확성이란 체계적(systematic) 으로 탐색을 하여 “방문하지 않은 정점이 남지 않게” 하는 것이다. 이를 위해서 미로 탐색(maze)과 마찬가지로, 한 번 간 길은 표시해두고, 어디까지 갔는지 기록해야 한다.
이때 정점의 상태를 표시(marking) 하는 것은 그래프 탐색에서 가장 중요한 개념 중 하나이다. 각 정점은 아래와 같아 항상 세 가지 상태 중 하나의 상태에 있다:
- undiscovered: 탐색이 시작되기 전, 아직 전혀 방문하지 않은 상태.
- discovered: 방문은 했지만, 그 정점에서 나가는 간선들을 아직 모두 확인하지 않은 상태.
- processed: 해당 정점의 모든 간선을 다 검사한 후 완전히 끝낸 상태.
이때, 그래프 탐색 과정에서 모든 정점은 undiscovered → discovered → processed 순서로 상태가 바뀐다. 이에 따라 DFS나 BFS 알고리즘에서는 이 상태를 배열로 관리한다. 따라서 발견했지만 아직 처리가 끝나지 않은 정점들을 저장하는 자료구조가 필요하며, BFS에서는 큐(Queue)를 , DFS에서는 스택(Stack)을 활용한다.
기본적인 탐색알고리즘의 절차는 아래와 같다:
- 처음엔 시작 정점 하나만 discovered 상태이며, 해당 정점을 꺼내서 모든 인접 정점을 확인한다.
- 새로 발견된 정점은 “discovered” 로 바꾸고 to-do list(큐/스택) 에 넣는다.
- 해당 정점의 모든 간선을 검사한 뒤에는 “processed” 상태로 바꾼다.
- to-do list 가 빌 때까지 계속 반복한다.
Minimum Spanning Trees
자세한 내용은 Minimum Spanning Trees 문서를 참조하십시오.
각주
- ↑ 해당 정점의 차수에 해당한다.
