다른 명령
새 문서: 분류:계산 이론 개론 분류:컴퓨터 공학 상위 문서: 계산 이론 개론 ==개요== Finite Automaton<ref>단수형이 automaton, 복수형이 automata이다.</ref>은 유한한 메모리를 가진 단순한 계산 장치를 수학적으로 모델링한 것이며, FSM(Finite State Machine)의 가장 기본적인 형태이다. 이는 단순한 계산 장치이며, "유한 메모리"이기 때문에 무한한 기억... |
잔글 봇: 자동으로 텍스트 교체 (-\[\[분류:컴퓨터 공학(\|[^\]]+)?\]\] +) |
||
| (다른 사용자 한 명의 중간 판 11개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
[[분류:계산 이론 개론]] | [[분류:계산 이론 개론]] | ||
상위 문서: [[계산 이론 개론#Finite Automata|계산 이론 개론]] | 상위 문서: [[계산 이론 개론#Finite Automata|계산 이론 개론]] | ||
| 19번째 줄: | 19번째 줄: | ||
===State Diagrams=== | ===State Diagrams=== | ||
[[파일:Figure 1. State Diagram.png|섬네일|Figure 1. State Diagram]] | |||
Finite automata는 상태 다이어그램(state diagram) 으로 시각적으로 표현할 수 있다. 이는 figure 1과 같이 표현된다. Figure 1에 나타난 예시 상태 다이어 그램을 해석하면 아래와 같다. | Finite automata는 상태 다이어그램(state diagram) 으로 시각적으로 표현할 수 있다. 이는 figure 1과 같이 표현된다. Figure 1에 나타난 예시 상태 다이어 그램을 해석하면 아래와 같다. | ||
* Q1: 시작 상태, 입력 0이 들어오면 Q1에 머무름, 1이 들어오면 Q2로 이동. | * Q1: 시작 상태, 입력 0이 들어오면 Q1에 머무름, 1이 들어오면 Q2로 이동. | ||
| 28번째 줄: | 29번째 줄: | ||
DFA(Deterministic Finite Automaton)은 아래와 같은 5-튜플(<math>Q, \Sigma, \delta, q_0, F</math>)로 정의할 수 있다: | DFA(Deterministic Finite Automaton)은 아래와 같은 5-튜플(<math>Q, \Sigma, \delta, q_0, F</math>)로 정의할 수 있다: | ||
* <math>Q</math>: 유한 상태 집합 | * <math>Q</math>: 유한 상태 집합 | ||
* <math>\Sigma</math>: 유한 입력 기호 집합 | * <math>\Sigma</math>: 유한 입력 기호 집합(입력 알파벳) | ||
* <math>\delta</math>: <math>Q\times \Sigma \rightarrow Q</math>: 전이 함수(transition function), 현재 상태와 입력 기호를 다음 상태로 매핑 | * <math>\delta</math>: <math>Q\times \Sigma \rightarrow Q</math>: 전이 함수(transition function), 현재 상태와 입력 기호를 다음 상태로 매핑 | ||
** <math>Q\times \Sigma</math>는 | ** <math>Q\times \Sigma</math>는 상태 집합과 알파벳 집합의 모든 가능한 쌍이며, 전이 함수 <math>\delta</math>는 이 쌍을 받아서 새로운 상태로 매핑하는 역할을 한다. 이때 전이 함수는 모든 (state, input) 쌍에 대해 하나의 출력만 존재해야 한다. 따라서 결정적(deterministic)이라고 한다. | ||
* <math>q_0 \in Q</math>: 시작 상태(start state) | * <math>q_0 \in Q</math>: 시작 상태(start state) | ||
* <math>F \subseteq Q</math>: 수용 상태 집합(accept states) | * <math>F \subseteq Q</math>: 수용 상태 집합(a set of accept states) | ||
이를 통해서 DFA M이 수용하는 어떤 문자열 집합 <math>w = w_1w_2\cdots w_n</math>일 때, <math>M = (Q, \Sigma, \delta, q_0, F)</math>이 <math>w</math>를 "수용"한다는 것은 아래와 같이 정의된다. | 이를 통해서 DFA M이 수용하는 어떤 문자열 집합 <math>w = w_1w_2\cdots w_n</math>일 때, <math>M = (Q, \Sigma, \delta, q_0, F)</math>이 <math>w</math>를 "수용"한다는 것은 아래와 같이 정의된다. | ||
어떤 순열 <math>r_0r_1r_2\cdots r_n</math>이 존재하여 아래의 조건을 만족한다. | 어떤 상태 순열(a sequence of states) <math>r_0r_1r_2\cdots r_n</math>이 존재하여 아래의 조건을 만족한다. | ||
1. 시작 상태: <math>r_0 = q_0</math> | 1. 시작 상태: <math>r_0 = q_0</math> | ||
2. 각 단계에서 <math>\delta(r_i, w_{i+1}) = r_{i+1}, i = 0,1,\cdots,n-1</math> | 2. 각 단계에서 <math>\delta(r_i, w_{i+1}) = r_{i+1}, i = 0,1,\cdots,n-1</math> | ||
3. <math>r_n \in F</math>: 문자열을 다 읽은 뒤 마지막 상태 <math>r_n</math>이 수용 상태 집합에 포함 | 3. <math>r_n \in F</math>: 문자열을 다 읽은 뒤 마지막 상태 <math>r_n</math>이 수용 상태 집합에 포함 | ||
이를 바탕으로 위 조건을 만족하는 문자열 <math>w</math>들의 | 이를 바탕으로 위 조건을 만족하는 문자열 <math>w</math>들의 집합은 M이 인식하는 언어(language recognized by M)이며, 아래와 같다: | ||
<math>L(M) = \{w\in \Sigma^*|M\,\, accepts\,\, w\}</math> | <math>L(M) = \{w\in \Sigma^*|M\,\, accepts\,\, w\}</math> | ||
이러한 언어는 [[Regular Languages|정규 언어(regular language)]]라고 정의된다. 정규 언어에 대한 자세한 내용은 [[Regular Languages]] 문서를 참조해 주십시오. | |||
==[[Nondeterministic Finite Automata]]== | |||
자세한 내용은 [[Nondeterministic Finite Automata]] 문서를 참조하십시오. | |||
==[[Generalized NFA]]== | |||
자세한 내용은 [[Generalized NFA]] 문서를 참조하십시오. | |||
==Equivalence of Automata== | |||
어떤 두 오토마타가 동일(equivalent)하다고 하기 위해서는 두 오토마타가 동일한 언어를 인식하면 된다. 이때 중요한 것은 아래의 정리이다: | |||
모든 NFA는 equivalent한 DFA를 가진다. | |||
사실 DFA는 NFA의 특수한 경우이며, DFA <math>\subseteq</math> NFA이다. 이는 DFA의 <math>\delta</math>를 <math>\delta '</math>로 바꾸어 집합 형태로 표현하면 NFA의 정의에 부합하기 때문이다. 즉, DFA는 ε-transition을 안 쓰고 항상 단일한 전이만 존재하는 NFA이다. | |||
이보다 더욱 중요한 것은, NFA와 DFA는 표현력(인식할 수 있는 언어)이 동일하다는 것이다. 즉, NFA든 DFA든 인식하면 정규 언어이다. DFA는 "동시에 여러 상태"에 있을 수 없지만, NFA는 여러 경로를 따라갈 수 있다. 따라서 DFA는 NFA의 가능한 모든 상태 집합의 각각의 원소를 하나의 상태로 취급한다. 즉, DFA의 상태 집합은 NFA 상태 집합의 멱집합(Powerset)이다. 따라서 NFA의 상태가 n개라면 DFA는 최대 2<sup>n</sup>개의 상태가 필요하다. 예를 들어 NFA의 상태 집합 Q가 <math>\{q_0,q_1,q_2\}</math>라면, DFA의 상태는 Q의 부분집합들 전체:<br><math>\mathcal{P}(Q) = \{\empty,\{q_0\},\{q_1\},\{q_2\},\{q_0,q_1\},\{q_1,q_2\},\{q_2, q_0\},\{q_0,q_1,q_2\}\}</math>이 된다. 즉, 원래는 3개의 상태밖에 없던 NFA가 DFA로 바뀌면 최대 8개의 상태를 가질 수 있다. | |||
이때 NFA <math>N = (Q, \Sigma, \delta, q_0, F)</math>가 주어졌을 때, equivalent한 DFA M은: | |||
* <math>M = (Q', \Sigma, \delta', q'_0, F')</math> | |||
* <math>Q' = \mathcal{P}(Q)</math>: NFA 상태들의 모든 부분 집합 | |||
* <math>F' = \{R\in Q' | R \cap F \ne \emptyset\}</math>: Accept 상태가 포함된 부분 집합들 | |||
* <math>q'_0 = E(\{q_0\})</math>: 시작 상태에서 ε-transition으로 도달 가능한 모든 상태 모음 | |||
* <math>\delta'(R, a) = \bigcup_{r\in R}E(\delta(r,a))</math>: DFA에서의 전이는 NFA의 여러 전이를 동시에 고려한 집합 | |||
이때 <math>E(R)</math>은 집합 R에서 시작해서 ε-transition만 따라갔을 때 도달 가능한 모든 상태를 의미한다. 이는 Powerset Construction에서 꼭 필요하다. 어떤 입력을 읽기 전에 미리 ε-transition으로 퍼질 수 있으니까, 이를 미리 포함해서 DFA 상태를 정의해야 하기 때문이다. | |||
[[파일:Figure 2. NFA example.png|섬네일|Figure 2. NFA example]] | |||
[[파일:Figure 3. DFA example.png|섬네일|Figure 3. DFA example]] | |||
Figure 2의 NFA 다이어그램은 figure 3의 DFA 다이어그램으로 변경될 수 있다. Figure 2를 분석하면 아래와 같다: | |||
<math>q'_0 = E({Q_1}) = \{Q_1, Q_2\}</math> | |||
<math>\delta'(\{Q_1, Q_2\}, 0) = E(\{Q_1, Q_3\}) = \{Q_1, Q_2, Q_3\}</math> | |||
<math>\delta'(\{Q_1, Q_2\}, 1) = E(\{Q_1, Q_3\}) = \{Q_1, Q_2, Q_3\}</math> | |||
<math>\delta'(\{Q_1, Q_2, Q_3\}, 0) = E(\{Q_1, Q_3\}) = \{Q_1, Q_2, Q_3\}</math> | |||
<math>\delta'(\{Q_1, Q_2, Q_3\}, 1) = E(\{Q_1, Q_3\}) = \{Q_1, Q_2, Q_3\}</math> | |||
즉, DFA는 사실상 2개의 상태만 가진다: | |||
<math>q_0 = \{Q_1, Q_2\}</math> | |||
<math>q_1 = \{Q_1, Q_2, Q_3\}</math> | |||
이에 따라 figure 3의 다이어그램이 만들어진다. 이때 accept state가 <math>q_1</math>인 이유는 원래 NFA의 accept state인 <math>Q_3</math>를 포함하기 때문이다. 따라서 DFA의 유일한 수용 상태는 <math>q_1</math>이다. 또한 원래 <math>\{Q_1, Q_2, Q_3\}</math>의 부분집합은 총 8개 이지만, 실제로 도달할 수 있는 것은 <math>\{Q_1, Q_2\}, \{Q_1, Q_2, Q_3\}</math> 두개 뿐이므로 나머지 6개 집합은 reachable하지 않고 DFA에서 무시해도 된다. | |||
==Other Ways to Model Computing Devices== | ==Other Ways to Model Computing Devices== | ||
2026년 1월 15일 (목) 15:20 기준 최신판
상위 문서: 계산 이론 개론
개요
Finite Automaton[1]은 유한한 메모리를 가진 단순한 계산 장치를 수학적으로 모델링한 것이며, FSM(Finite State Machine)의 가장 기본적인 형태이다. 이는 단순한 계산 장치이며, "유한 메모리"이기 때문에 무한한 기억이나 복잡한 연산이 불가능하고, 오직 현재 상태와 입력에 따라 동작만 결정된다는 특징이 있지만, 다양한 활용 분야를 가지고 있다. 예를 들어 자판기, 엘리베이터, 가전제품과 같은 단순 동작 장치들은 모두 finite automata로 모델링될 수 있다. 이들은 현재 상태(예: 금액 투입 상태, 층 수, 전원 상태)에 따라 행동을 정한다. 또한 텍스트 에디터, 스팸 필터, 검색 엔진, 컴파일러 등은 문자열 패턴 매칭 문제를 해결하기 위해 해당 원리를 사용한다. 중요한 것은 모든 실제 컴퓨터도 유한한 메모리를 가지므로, 이론적으로는 finite automaton이라고 볼 수 있다.
Finite Automata as Language Recognizers
Finite automata는 문자열(언어)을 인식하는 기계로 이해할 수 있으며, 이는 아래와 같은 구성 요소로 이뤄 진다:
- Finite Control: 현재 내부 상태를 저장하는 장치.
- Input Tape: 기계에 주어지는 입력 문자열이 있는 테이프.
- Read Head: 입력 테이프에서 현재 어떤 위치(문자)를 읽고 있는지 가리키는 지시자.
이러한 finite automata는 아래와 같은 단계를 거쳐 작동한다:
- 문자열을 왼쪽에서 오른쪽으로 차례대로 한 글자씩 읽음.
- 각 단계에서 finite control이 현재 상태와 입력 문자에 따라 "다음 상태"를 결정.
- 입력 문자열 끝까지 다 읽으면, current state에 따라 문자열을 수용(accepted) 또는 거부(rejected).
이때 어떤 finite automaton이 수용하는 모든 문자열 집합을 그 automaton이 인식(recognize)하는 언어라고 부른다.
State Diagrams
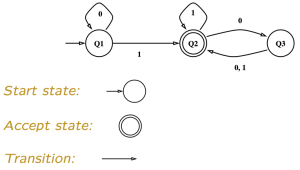
Finite automata는 상태 다이어그램(state diagram) 으로 시각적으로 표현할 수 있다. 이는 figure 1과 같이 표현된다. Figure 1에 나타난 예시 상태 다이어 그램을 해석하면 아래와 같다.
- Q1: 시작 상태, 입력 0이 들어오면 Q1에 머무름, 1이 들어오면 Q2로 이동.
- Q2: 수용 상태, 입력 1이면 Q2에 머무르고, 0이면 Q3으로 이동.
- Q3: 수용 상태 아님, 입력(0,1) 모두 다시 Q2로 돌아감.
즉, 해당 finite automata는 마지막 입력이 1, 혹은 0이 문자열 끝에 짝수개 만큼 있으면 해당 문자열을 수용한다.
Formal Definition of Finite Automaton
DFA(Deterministic Finite Automaton)은 아래와 같은 5-튜플([math]\displaystyle{ Q, \Sigma, \delta, q_0, F }[/math])로 정의할 수 있다:
- [math]\displaystyle{ Q }[/math]: 유한 상태 집합
- [math]\displaystyle{ \Sigma }[/math]: 유한 입력 기호 집합(입력 알파벳)
- [math]\displaystyle{ \delta }[/math]: [math]\displaystyle{ Q\times \Sigma \rightarrow Q }[/math]: 전이 함수(transition function), 현재 상태와 입력 기호를 다음 상태로 매핑
- [math]\displaystyle{ Q\times \Sigma }[/math]는 상태 집합과 알파벳 집합의 모든 가능한 쌍이며, 전이 함수 [math]\displaystyle{ \delta }[/math]는 이 쌍을 받아서 새로운 상태로 매핑하는 역할을 한다. 이때 전이 함수는 모든 (state, input) 쌍에 대해 하나의 출력만 존재해야 한다. 따라서 결정적(deterministic)이라고 한다.
- [math]\displaystyle{ q_0 \in Q }[/math]: 시작 상태(start state)
- [math]\displaystyle{ F \subseteq Q }[/math]: 수용 상태 집합(a set of accept states)
이를 통해서 DFA M이 수용하는 어떤 문자열 집합 [math]\displaystyle{ w = w_1w_2\cdots w_n }[/math]일 때, [math]\displaystyle{ M = (Q, \Sigma, \delta, q_0, F) }[/math]이 [math]\displaystyle{ w }[/math]를 "수용"한다는 것은 아래와 같이 정의된다.
어떤 상태 순열(a sequence of states) [math]\displaystyle{ r_0r_1r_2\cdots r_n }[/math]이 존재하여 아래의 조건을 만족한다. 1. 시작 상태: [math]\displaystyle{ r_0 = q_0 }[/math] 2. 각 단계에서 [math]\displaystyle{ \delta(r_i, w_{i+1}) = r_{i+1}, i = 0,1,\cdots,n-1 }[/math] 3. [math]\displaystyle{ r_n \in F }[/math]: 문자열을 다 읽은 뒤 마지막 상태 [math]\displaystyle{ r_n }[/math]이 수용 상태 집합에 포함
이를 바탕으로 위 조건을 만족하는 문자열 [math]\displaystyle{ w }[/math]들의 집합은 M이 인식하는 언어(language recognized by M)이며, 아래와 같다:
[math]\displaystyle{ L(M) = \{w\in \Sigma^*|M\,\, accepts\,\, w\} }[/math]
이러한 언어는 정규 언어(regular language)라고 정의된다. 정규 언어에 대한 자세한 내용은 Regular Languages 문서를 참조해 주십시오.
Nondeterministic Finite Automata
자세한 내용은 Nondeterministic Finite Automata 문서를 참조하십시오.
Generalized NFA
자세한 내용은 Generalized NFA 문서를 참조하십시오.
Equivalence of Automata
어떤 두 오토마타가 동일(equivalent)하다고 하기 위해서는 두 오토마타가 동일한 언어를 인식하면 된다. 이때 중요한 것은 아래의 정리이다:
모든 NFA는 equivalent한 DFA를 가진다.
사실 DFA는 NFA의 특수한 경우이며, DFA [math]\displaystyle{ \subseteq }[/math] NFA이다. 이는 DFA의 [math]\displaystyle{ \delta }[/math]를 [math]\displaystyle{ \delta ' }[/math]로 바꾸어 집합 형태로 표현하면 NFA의 정의에 부합하기 때문이다. 즉, DFA는 ε-transition을 안 쓰고 항상 단일한 전이만 존재하는 NFA이다.
이보다 더욱 중요한 것은, NFA와 DFA는 표현력(인식할 수 있는 언어)이 동일하다는 것이다. 즉, NFA든 DFA든 인식하면 정규 언어이다. DFA는 "동시에 여러 상태"에 있을 수 없지만, NFA는 여러 경로를 따라갈 수 있다. 따라서 DFA는 NFA의 가능한 모든 상태 집합의 각각의 원소를 하나의 상태로 취급한다. 즉, DFA의 상태 집합은 NFA 상태 집합의 멱집합(Powerset)이다. 따라서 NFA의 상태가 n개라면 DFA는 최대 2n개의 상태가 필요하다. 예를 들어 NFA의 상태 집합 Q가 [math]\displaystyle{ \{q_0,q_1,q_2\} }[/math]라면, DFA의 상태는 Q의 부분집합들 전체:
[math]\displaystyle{ \mathcal{P}(Q) = \{\empty,\{q_0\},\{q_1\},\{q_2\},\{q_0,q_1\},\{q_1,q_2\},\{q_2, q_0\},\{q_0,q_1,q_2\}\} }[/math]이 된다. 즉, 원래는 3개의 상태밖에 없던 NFA가 DFA로 바뀌면 최대 8개의 상태를 가질 수 있다.
이때 NFA [math]\displaystyle{ N = (Q, \Sigma, \delta, q_0, F) }[/math]가 주어졌을 때, equivalent한 DFA M은:
* [math]\displaystyle{ M = (Q', \Sigma, \delta', q'_0, F') }[/math] * [math]\displaystyle{ Q' = \mathcal{P}(Q) }[/math]: NFA 상태들의 모든 부분 집합 * [math]\displaystyle{ F' = \{R\in Q' | R \cap F \ne \emptyset\} }[/math]: Accept 상태가 포함된 부분 집합들 * [math]\displaystyle{ q'_0 = E(\{q_0\}) }[/math]: 시작 상태에서 ε-transition으로 도달 가능한 모든 상태 모음 * [math]\displaystyle{ \delta'(R, a) = \bigcup_{r\in R}E(\delta(r,a)) }[/math]: DFA에서의 전이는 NFA의 여러 전이를 동시에 고려한 집합
이때 [math]\displaystyle{ E(R) }[/math]은 집합 R에서 시작해서 ε-transition만 따라갔을 때 도달 가능한 모든 상태를 의미한다. 이는 Powerset Construction에서 꼭 필요하다. 어떤 입력을 읽기 전에 미리 ε-transition으로 퍼질 수 있으니까, 이를 미리 포함해서 DFA 상태를 정의해야 하기 때문이다.
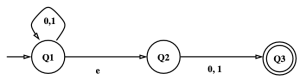
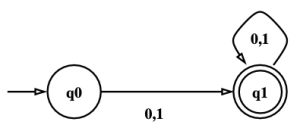
Figure 2의 NFA 다이어그램은 figure 3의 DFA 다이어그램으로 변경될 수 있다. Figure 2를 분석하면 아래와 같다:
[math]\displaystyle{ q'_0 = E({Q_1}) = \{Q_1, Q_2\} }[/math] [math]\displaystyle{ \delta'(\{Q_1, Q_2\}, 0) = E(\{Q_1, Q_3\}) = \{Q_1, Q_2, Q_3\} }[/math] [math]\displaystyle{ \delta'(\{Q_1, Q_2\}, 1) = E(\{Q_1, Q_3\}) = \{Q_1, Q_2, Q_3\} }[/math] [math]\displaystyle{ \delta'(\{Q_1, Q_2, Q_3\}, 0) = E(\{Q_1, Q_3\}) = \{Q_1, Q_2, Q_3\} }[/math] [math]\displaystyle{ \delta'(\{Q_1, Q_2, Q_3\}, 1) = E(\{Q_1, Q_3\}) = \{Q_1, Q_2, Q_3\} }[/math]
즉, DFA는 사실상 2개의 상태만 가진다:
[math]\displaystyle{ q_0 = \{Q_1, Q_2\} }[/math] [math]\displaystyle{ q_1 = \{Q_1, Q_2, Q_3\} }[/math]
이에 따라 figure 3의 다이어그램이 만들어진다. 이때 accept state가 [math]\displaystyle{ q_1 }[/math]인 이유는 원래 NFA의 accept state인 [math]\displaystyle{ Q_3 }[/math]를 포함하기 때문이다. 따라서 DFA의 유일한 수용 상태는 [math]\displaystyle{ q_1 }[/math]이다. 또한 원래 [math]\displaystyle{ \{Q_1, Q_2, Q_3\} }[/math]의 부분집합은 총 8개 이지만, 실제로 도달할 수 있는 것은 [math]\displaystyle{ \{Q_1, Q_2\}, \{Q_1, Q_2, Q_3\} }[/math] 두개 뿐이므로 나머지 6개 집합은 reachable하지 않고 DFA에서 무시해도 된다.
Other Ways to Model Computing Devices
유한 오토마타를 언어 인식기(language recognizer)로만 인식할 수 있는 것은 아니며, 아래와 같이 간주할 수 있다:
- Language generators: 입력을 소비(consuming)하는 대신 기호를 생성(emitting)하는 모델.
- Transducers: 기호를 읽으면서 동시에 다른 기호를 출력.
- Interactive: 환경과 상호작용(interaction)하면서 동작하는 오토마타.
각주
- ↑ 단수형이 automaton, 복수형이 automata이다.
