다른 명령
| (같은 사용자의 중간 판 7개는 보이지 않습니다) | |||
| 24번째 줄: | 24번째 줄: | ||
==Hash Functions== | ==Hash Functions== | ||
해시 함수(Hash function)의 가장 중요한 역할은 사전 자료구조 원소의 키(key) 를 정수(integer) 로 변환하는 것이다. 예를 들면 키가 "apple"일 때, 이를 어떤 정수값으로 바꾸는 것이다. 이때 좋은 해시 함수의 조건은 아래와 같다: | |||
# 계산이 저렴해야 함(Is cheap to evaluate)<br>해시 함수가 복잡하면 해시 테이블을 쓰는 의미가 없으므로, 빠르고 단순하게 변환해야 한다. | |||
# 모든 해시 테이블 슬롯을 고르게 사용(Tends to use all positions from 0 … M uniformly)<br>해시 테이블의 크기가 M이라면, 해시 함수의 결과로 인덱스 0부터 M-1까지 고르게 값이 나와야 충돌(collisions)이 줄어든다. | |||
아래는 문자열 키를 정수로 바꾸는 어떤 해시 함수이다: | |||
<math>h=\sum^{Key\,Length}_{i=0}128^i\times char(key[i])</math> | |||
위와 같은 해시 함수의 결과로는 매우 큰 정수가 나올 수 있다. 만약 해시 함수의 결과가 1,928,374,982 같은 수라면, 해시 테이블 크기보다 훨씬 클 수 있다. 따라서 해당 결과를 테이블 크기에 맞게 줄이는 작업을 해야 한다. 이는 아래와 같은 방법을 사용한다. | |||
<math>h(k) = k\, mod\, M</math> | |||
위에서 k는 해시 함수를 통해 1차적으로 얻은 큰 정수를 의미하며, M은 해시 테이블의 크기를 의미하며, 모듈러 연산을 통해 결과값이 항상 0~k-1 범위 내에 있도록 한다. 이때 M의 값은 2<sup>i</sup>-1<ref>i는 k를 이진수로 표현하였을 때 필요한 비트의 수를 의미하며, 2<sup>i</sup>-1은 i개의 비트로 만들 수 있는 가장 큰 수에 해당한다.</ref>에 너무 가깝지 않은 M은 큰 소수로 선택하는 것이 권장된다. 만약 M을 2의 거듭제곱수로 사용한다면, k를 이진수로 바꾸었을 때 하위 비트만을 이용하므로 충돌이 증가한다. 또한 M이 소수가 아니라면, 키 값이 특정 배수 패턴을 가질 때 특정 버킷들에 모이므로 충돌이 늘어난다. | |||
<math></math> | 예를 들어, 사회보장번호(SSN)의 앞 세 자리를 해시 키로 쓰는 경우는 나쁜 해시 함수이다. 그 이유는 사회보장번호 앞 세 자리는 지역이나 특정 규칙에 따라 배정되므로 값이 편향되어 있기 때문이다.<ref>주민등록번호의 경우에도 2020년 법 개정 이전에는 앞 여섯 자리는 성별과 출생 주소지 등에 대한 정보를 담고 있으므로 나쁜 해시 함수로 볼 수 있다.</ref> 하지만 SSN의 뒷 세 자리를 해시 키로 쓰는 경우는 좋은데, 마지막 세 자리는 지역과 상관없이 거의 무작위(random)로 배정되므로 훨씬 균일한 분포를 보이기 때문이다. | ||
<math></math> | |||
===The Birthday Paradox=== | |||
아무리 좋은 해시 함수를 사용하더라도 충돌은 피하기 힘들다. 그 이유는 birthday paradox 때문인데, 이는 23명만 모여도 생일이 같은 두 사람이 있을 확률이 50% 이상이 된다는 것이다. 이는 삽입할 때마다 충돌 확률은 누적되어 올라가기 때문이다. 해시 테이블의 크기가 m일 때 n개의 키를 삽입하면 아래와 같은 충돌 확률을 가진다: | |||
<math>P(no collision) = \frac{m}{m} \times \frac{m-1}{m} \times \frac{m-2}{m} \times \cdots \times \frac{m-n+1}{m} = \prod^{n-1}_{i=0}\frac{m-i}{m}</math> | |||
==Applications of Hashing== | |||
===Performance on Set Operations=== | |||
해시 테이블을 이용한 딕셔너리 연산들의 성능을 분석하면 아래와 같다: | |||
* Search (탐색)<br>기대 성능(Expected): O(1) <math>\rightarrow</math> 해시 함수가 키를 고르게 분산한다면 평균적으로 한 번에 원하는 원소를 찾을 수 있음.<br>최악의 경우(Worst case): O(n) <math>\rightarrow</math> 모든 원소가 같은 버킷에 몰려 linked list처럼 되면 전체를 다 탐색해야 함 | |||
* Insert (삽입)<br>기대 성능(Expected): O(1) <math>\rightarrow</math> 해시 함수 계산 후 그 자리에 넣기만 하면 됨.<br>최악의 경우(Worst case): O(n) <math>\rightarrow</math> 충돌이 많이 나서 특정 버킷에 길게 쌓이면 삽입도 느려짐. | |||
* Delete (삭제)<br>기대 성능(Expected): O(1) <math>\rightarrow</math> 원소를 찾고 삭제하면 끝.<br>최악의 경우(Worst case): O(n) | |||
* Min / Max / Predecessor / Successor: <math>\Theta(n+m)</math> <math>\rightarrow</math> 해시 테이블은 정렬 구조가 아니기 때문에 최솟값/최댓값이나 이전/다음 원소 같은 연산은 효율적으로 할 수 없기 때문. | |||
정리하자면, 해시 테이블은 탐색/삽입/삭제 연산에 평균적으로 매우 빠른 시간 복잡도를 제공한다. 하지만 최악의 경우 시간 복잡도는 선형적으로 늘어나기 때문에, 성능은 예측 불가능하다고 말할 수 있다. 따라서 보다 안정적인 성능의 연산을 사용하고자 할 때에는 [[Binary Search Tree|균형 이진 탐색 트리(Balanced Binary Search Tree)]]가 더욱 낫다. | |||
===Hashing in Managing Big Files/Data=== | |||
Google의 Udi Manber는 "구글의 세 가지 중요한 알고리즘은 hashing, hashing, hashing"이라고 말한 적이 있다. 이는 해싱이 검색과 데이터 처리에서 매우 큰 역할을 한다는 것을 알려준다. 이는 해싱이 큰 데이터를 짧고 독특한 해시 코드로 표현할 수 있다는 특징 때문이다. 이러한 해싱의 특징은 문서 유서도를 판별하거나 표절을 감지하는데에도 사용된다. 새 문서를 해시하여 기존 문서들의 해시와 비교했을 때 같은 해시 값이 존재한다면 중복 문서로 판단하는 것이다. 또한 문서를 여러 겹치는 구간(window)로 나누어 해시를 하고, 이를 비교하는데 사용하여 해시 충돌이 있다면 표절로 볼 수 있다. | |||
===Integrity Checking=== | |||
파일이 변조되지 않았음을 확인하는 방법으로는 암호학적 해시(cryptographic hash)가 있다. 이는 어떤 파일의 해시를 처음 계산해 기록해 둔 후, 나중에 다시 해시를 계산했을 때 값이 동일하면 파일이 변하지 않은 것이다. 단 1바이트라도 바뀌면 해시 값이 완전히 달라진다. 이는 소프트웨어 배포 시 SHA-256 해시를 제공하여 다운로드 받은 파일의 해시를 비교해 변조 여부 확인하는 방식으로 활용된다. | |||
===Hashing as a Representation=== | |||
목적에 맞게 디자인된 해싱 함수(Custom-designed Hashing)는 원소들을 버킷에 표준화된 표현(cannonical representation)으로 저장하는데 사용될 수 있다. 예를 들면, "skiena"와 같은 단어를 알파벳 순으로 정렬하면 "aeikns"가 되는데, 이러한 해싱은 같은 글자들로 이뤄진 단어들을 같은 해시 버킷에 모으는데 활용될 수 있다. 이 역시 예를 들자면 "dog"와 "god"는 같은 문자로 이루어져 있으므로, "dgo"를 의미하는 버킷에 담긴다. 이러한 방식은 비슷한 것끼리 같은 버킷에 모으는 proximity-preserving hashing이라고 한다. | |||
==The Rabin-Karp Algorithm== | |||
Substring Pattern Matching 문제는 아래와 같은 형식을 가지는 문제이다: | |||
Input: 텍스트 문자열 t 와 패턴 문자열 p | |||
문제: t 안에 p가 부분 문자열로 존재하는가? 존재한다면 어디에 있는가? | |||
예를 들면, 성경에 "Skiena"라는 단어가 존재하는지 찾는 문제이다. 이 문제를 해결하는 가장 단순한 방법은 브루트 포스 탐색(Brute Force Search)이다. 이는 p를 t의 각 위치에 겹쳐놓고, 문자가 모두 일치하는지 검사하는 방식이다. 이때 t의 길이가 n, p의 길이가 m이라면 시간 복잡도는 O(nm)이다. | |||
이를 조금 더 빠르게 해결하기 위해서 해싱을 활용하여 문자열을 해시 값으로 바꾸어 비교할 수 있다. 이는 아래와 같은 방식으로 동작한다: | |||
# p의 해시 값을 계산한다. | |||
# t의 길이가 m인 부분 문자열들의 해시값을 계산한다. | |||
# 해시값이 같으면 문자열이 같을 가능성이 높으므로 직접 비교해서 최종 확인한다. | |||
이는 문자열 전체를 비교하지 않고, 해시값만 비교하므로 더욱 빠르다. 하지만 서로 다른 문자열인데 해시값이 같아지는 경우에는 오류 가능성이 있다. 하지만 좋은 해시 함수를 사용한다면 그 확률은 매우 낮다. 해당 알고리즘은 시간 복잡도는 아래와 같이 계산된다. | |||
부분 문자열 개수 = n - m + 1 | |||
각 부분 문자열의 해시 계산 비용 = O(m) | |||
전체 시간 복잡도: O(mn) | |||
따라서 여전히 전체 복잡도는 O(mn)으로 브루트 포스 알고리즘과 일치한다. | |||
===The Rabin-Karp Algorithm=== | |||
The Rabin-Karp Algorithm은 해시값을 재활용하여 더욱 빠르게 해시 함수를 실행하는 알고리즘이다. 해당 알고리즘에서는 해시 함수를 아래와 같이 정의한다: | |||
<math>H(S, j) = \sum^{m-1}_{i=0}\alpha^{m-(i+1)}\times char(s_{i+j})</math><ref>H(S, j)는 문자열 S의 j번째 위치에서 시작하는 길이 m의 부분 문자열의 해시값을 의미한다.</ref><ref><math>\alpha</math>는 보통 큰 수이며, 위치에 따라 가중치를 주는데 사용된다.</ref> | |||
<math>H(S, j+1) = (H(S, j)-\alpha^{m-1}char(s_j))\cdot \alpha + s_{j+m}</math> | |||
이는 j 번째 해시값을 알고 있다면, j+1 번째 해시값을 상수 시간 O(1) 연산만으로 계산할 수 있다는 것을 의미한다. 이 경우 전체 시간 복잡도는 아래와 같이 계산된다: | |||
O(n): 각 부분 문자열에 대해 해시값 업데이트 | |||
O(m): 탐색할 패턴의 해시값 계산 | |||
총 O(n + m) | |||
즉, Rabin-Karp 알고리즘은 Brute Force보다 훨씬 효율적인 문자열 검색 방법이다. | |||
==각주== | ==각주== | ||
2025년 9월 24일 (수) 22:02 기준 최신판
상위 문서: Data Structures
개요
해시 테이블(Hash Table)은 사전(Dictionary)을 구현하는 데에 매우 실용적인 자료 구조이다. 해시 테이블의 근본적인 아이디어는 배열에서 인덱스만 주어지면 이를 바탕으로 원하는 원소에 즉시 접근할 수 있다는 것이다. 이때 키(key)는 보통 정수(integer)가 아니므로, 임의의 키를 정수 인덱스로 바꾸는 해시 함수(hash function)를 구현하고 응용하는 것이 해시 테이블의 골자이다.
Collisions
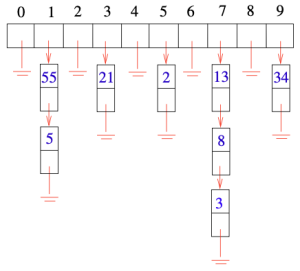
충돌(Collision)이란 서로 다른 두 키가 동일한 해시 값에 매핑되는 현상이다. 충돌이 발생할 경우에는 해당 버킷 안에 여러 키가 모이게 된다. 이때 키들이 해시 함수에 의해 균등(uniformly)하게 버킷들에 분포된다면, 각 버킷에는 몇 안되는 원소들만 들어간다. 따라서 이 경우에는 각 버킷 내부의 작은 리스트만 탐색하면 되므로 여전히 효율적이다. Figure 1은 해시 테이블의 크기가 10인 자료구조에 키 55, 21, 2, 13, 34, 5, 8, 3 등이 해시 값에 따라 여러 버킷에 들어가 있는 것을 보여준다.
Collision Resolution by Chaining
Chaining은 충돌이 발생하였을 때 이를 해결하는 방법중 하나로, 각 버킷마다 연결 리스트(linked list)를 두어 충돌이 발생할 때마다 새 원소를 해당 버킷의 리스트에 추가하는 방식이다. 이는 구현이 단순하고 직관적이라는 장점이 존재하지만, 각 리스트가 포인터를 필요로 하므로 메모리 낭비가 발생한다는 단점이 있다.[1] Figure 1은 Chaining의 한 예시로, 버킷에 해당하는 키 값들이 포인터를 통해 연결되어 있다.
시간 복잡도는 삽입/삭제/탐색 연산이 모두 리스트에서 처리되므로 리스트 길이에 비례한다. 이때 리스트의 길이는 평균적으로 [math]\displaystyle{ n/m }[/math][2]이므로 따라서 시간복잡도는 [math]\displaystyle{ O(n/m) }[/math]이다. 이때 [math]\displaystyle{ n/m }[/math]은 적재율(load factor)라고 불린다.
Open Addressing
Open addressing은 체이닝 대신 포인터를 쓰지 않고, 테이블 내부에서 다른 빈 공간을 찾아 저장하는 방식이다. 해당 방식은 원래의 해시 값이 가리키는 칸이 비어 있으면 삽입하고, 이미 차 있으면 다음 위치에 삽입하는 것을 시도하는 방식이다. 이때 충돌할 경우 다음 위치를 정하는 규칙은 아래와 같다:
- Sequentially: h,h+1,h+2,...
- Quadratically: h, h+12, h+22, h+32, ...
- Linearly: h, h+k, h+2k, h+3k, ...
Figure 2는 linear probing 방식의 한 예시를 보여준다. 해당 방식은 별도의 포인터 저장이 불필요하다는 장점이 있지만, 원소들이 뭉쳐서 연속 구간을 차지하면(Primary Clustering) 탐색 성능이 저하된다는 단점이 있다. 또한 해당 방식은 원소를 삭제할 때 어려움을 겪는데, 이는 원소를 삭제할 때 단순히 해당 칸을 비워버리면 문제가 생기기 때문이다. 왜냐하면 삭제 이후 탐색 시 “그 원소가 충돌 때문에 다른 칸에 있는지” 구분이 불가능해져서[3], 일부 원소가 검색 불가능해지기 때문이다. 따라서 보통은 “삭제된 자리”를 특별한 마커(예: DELETED flag)로 표시해 해결한다.
Hash Functions
해시 함수(Hash function)의 가장 중요한 역할은 사전 자료구조 원소의 키(key) 를 정수(integer) 로 변환하는 것이다. 예를 들면 키가 "apple"일 때, 이를 어떤 정수값으로 바꾸는 것이다. 이때 좋은 해시 함수의 조건은 아래와 같다:
- 계산이 저렴해야 함(Is cheap to evaluate)
해시 함수가 복잡하면 해시 테이블을 쓰는 의미가 없으므로, 빠르고 단순하게 변환해야 한다. - 모든 해시 테이블 슬롯을 고르게 사용(Tends to use all positions from 0 … M uniformly)
해시 테이블의 크기가 M이라면, 해시 함수의 결과로 인덱스 0부터 M-1까지 고르게 값이 나와야 충돌(collisions)이 줄어든다.
아래는 문자열 키를 정수로 바꾸는 어떤 해시 함수이다:
[math]\displaystyle{ h=\sum^{Key\,Length}_{i=0}128^i\times char(key[i]) }[/math]
위와 같은 해시 함수의 결과로는 매우 큰 정수가 나올 수 있다. 만약 해시 함수의 결과가 1,928,374,982 같은 수라면, 해시 테이블 크기보다 훨씬 클 수 있다. 따라서 해당 결과를 테이블 크기에 맞게 줄이는 작업을 해야 한다. 이는 아래와 같은 방법을 사용한다.
[math]\displaystyle{ h(k) = k\, mod\, M }[/math]
위에서 k는 해시 함수를 통해 1차적으로 얻은 큰 정수를 의미하며, M은 해시 테이블의 크기를 의미하며, 모듈러 연산을 통해 결과값이 항상 0~k-1 범위 내에 있도록 한다. 이때 M의 값은 2i-1[4]에 너무 가깝지 않은 M은 큰 소수로 선택하는 것이 권장된다. 만약 M을 2의 거듭제곱수로 사용한다면, k를 이진수로 바꾸었을 때 하위 비트만을 이용하므로 충돌이 증가한다. 또한 M이 소수가 아니라면, 키 값이 특정 배수 패턴을 가질 때 특정 버킷들에 모이므로 충돌이 늘어난다.
예를 들어, 사회보장번호(SSN)의 앞 세 자리를 해시 키로 쓰는 경우는 나쁜 해시 함수이다. 그 이유는 사회보장번호 앞 세 자리는 지역이나 특정 규칙에 따라 배정되므로 값이 편향되어 있기 때문이다.[5] 하지만 SSN의 뒷 세 자리를 해시 키로 쓰는 경우는 좋은데, 마지막 세 자리는 지역과 상관없이 거의 무작위(random)로 배정되므로 훨씬 균일한 분포를 보이기 때문이다.
The Birthday Paradox
아무리 좋은 해시 함수를 사용하더라도 충돌은 피하기 힘들다. 그 이유는 birthday paradox 때문인데, 이는 23명만 모여도 생일이 같은 두 사람이 있을 확률이 50% 이상이 된다는 것이다. 이는 삽입할 때마다 충돌 확률은 누적되어 올라가기 때문이다. 해시 테이블의 크기가 m일 때 n개의 키를 삽입하면 아래와 같은 충돌 확률을 가진다:
[math]\displaystyle{ P(no collision) = \frac{m}{m} \times \frac{m-1}{m} \times \frac{m-2}{m} \times \cdots \times \frac{m-n+1}{m} = \prod^{n-1}_{i=0}\frac{m-i}{m} }[/math]
Applications of Hashing
Performance on Set Operations
해시 테이블을 이용한 딕셔너리 연산들의 성능을 분석하면 아래와 같다:
- Search (탐색)
기대 성능(Expected): O(1) [math]\displaystyle{ \rightarrow }[/math] 해시 함수가 키를 고르게 분산한다면 평균적으로 한 번에 원하는 원소를 찾을 수 있음.
최악의 경우(Worst case): O(n) [math]\displaystyle{ \rightarrow }[/math] 모든 원소가 같은 버킷에 몰려 linked list처럼 되면 전체를 다 탐색해야 함 - Insert (삽입)
기대 성능(Expected): O(1) [math]\displaystyle{ \rightarrow }[/math] 해시 함수 계산 후 그 자리에 넣기만 하면 됨.
최악의 경우(Worst case): O(n) [math]\displaystyle{ \rightarrow }[/math] 충돌이 많이 나서 특정 버킷에 길게 쌓이면 삽입도 느려짐. - Delete (삭제)
기대 성능(Expected): O(1) [math]\displaystyle{ \rightarrow }[/math] 원소를 찾고 삭제하면 끝.
최악의 경우(Worst case): O(n) - Min / Max / Predecessor / Successor: [math]\displaystyle{ \Theta(n+m) }[/math] [math]\displaystyle{ \rightarrow }[/math] 해시 테이블은 정렬 구조가 아니기 때문에 최솟값/최댓값이나 이전/다음 원소 같은 연산은 효율적으로 할 수 없기 때문.
정리하자면, 해시 테이블은 탐색/삽입/삭제 연산에 평균적으로 매우 빠른 시간 복잡도를 제공한다. 하지만 최악의 경우 시간 복잡도는 선형적으로 늘어나기 때문에, 성능은 예측 불가능하다고 말할 수 있다. 따라서 보다 안정적인 성능의 연산을 사용하고자 할 때에는 균형 이진 탐색 트리(Balanced Binary Search Tree)가 더욱 낫다.
Hashing in Managing Big Files/Data
Google의 Udi Manber는 "구글의 세 가지 중요한 알고리즘은 hashing, hashing, hashing"이라고 말한 적이 있다. 이는 해싱이 검색과 데이터 처리에서 매우 큰 역할을 한다는 것을 알려준다. 이는 해싱이 큰 데이터를 짧고 독특한 해시 코드로 표현할 수 있다는 특징 때문이다. 이러한 해싱의 특징은 문서 유서도를 판별하거나 표절을 감지하는데에도 사용된다. 새 문서를 해시하여 기존 문서들의 해시와 비교했을 때 같은 해시 값이 존재한다면 중복 문서로 판단하는 것이다. 또한 문서를 여러 겹치는 구간(window)로 나누어 해시를 하고, 이를 비교하는데 사용하여 해시 충돌이 있다면 표절로 볼 수 있다.
Integrity Checking
파일이 변조되지 않았음을 확인하는 방법으로는 암호학적 해시(cryptographic hash)가 있다. 이는 어떤 파일의 해시를 처음 계산해 기록해 둔 후, 나중에 다시 해시를 계산했을 때 값이 동일하면 파일이 변하지 않은 것이다. 단 1바이트라도 바뀌면 해시 값이 완전히 달라진다. 이는 소프트웨어 배포 시 SHA-256 해시를 제공하여 다운로드 받은 파일의 해시를 비교해 변조 여부 확인하는 방식으로 활용된다.
Hashing as a Representation
목적에 맞게 디자인된 해싱 함수(Custom-designed Hashing)는 원소들을 버킷에 표준화된 표현(cannonical representation)으로 저장하는데 사용될 수 있다. 예를 들면, "skiena"와 같은 단어를 알파벳 순으로 정렬하면 "aeikns"가 되는데, 이러한 해싱은 같은 글자들로 이뤄진 단어들을 같은 해시 버킷에 모으는데 활용될 수 있다. 이 역시 예를 들자면 "dog"와 "god"는 같은 문자로 이루어져 있으므로, "dgo"를 의미하는 버킷에 담긴다. 이러한 방식은 비슷한 것끼리 같은 버킷에 모으는 proximity-preserving hashing이라고 한다.
The Rabin-Karp Algorithm
Substring Pattern Matching 문제는 아래와 같은 형식을 가지는 문제이다:
Input: 텍스트 문자열 t 와 패턴 문자열 p 문제: t 안에 p가 부분 문자열로 존재하는가? 존재한다면 어디에 있는가?
예를 들면, 성경에 "Skiena"라는 단어가 존재하는지 찾는 문제이다. 이 문제를 해결하는 가장 단순한 방법은 브루트 포스 탐색(Brute Force Search)이다. 이는 p를 t의 각 위치에 겹쳐놓고, 문자가 모두 일치하는지 검사하는 방식이다. 이때 t의 길이가 n, p의 길이가 m이라면 시간 복잡도는 O(nm)이다.
이를 조금 더 빠르게 해결하기 위해서 해싱을 활용하여 문자열을 해시 값으로 바꾸어 비교할 수 있다. 이는 아래와 같은 방식으로 동작한다:
- p의 해시 값을 계산한다.
- t의 길이가 m인 부분 문자열들의 해시값을 계산한다.
- 해시값이 같으면 문자열이 같을 가능성이 높으므로 직접 비교해서 최종 확인한다.
이는 문자열 전체를 비교하지 않고, 해시값만 비교하므로 더욱 빠르다. 하지만 서로 다른 문자열인데 해시값이 같아지는 경우에는 오류 가능성이 있다. 하지만 좋은 해시 함수를 사용한다면 그 확률은 매우 낮다. 해당 알고리즘은 시간 복잡도는 아래와 같이 계산된다.
부분 문자열 개수 = n - m + 1 각 부분 문자열의 해시 계산 비용 = O(m) 전체 시간 복잡도: O(mn)
따라서 여전히 전체 복잡도는 O(mn)으로 브루트 포스 알고리즘과 일치한다.
The Rabin-Karp Algorithm
The Rabin-Karp Algorithm은 해시값을 재활용하여 더욱 빠르게 해시 함수를 실행하는 알고리즘이다. 해당 알고리즘에서는 해시 함수를 아래와 같이 정의한다:
[math]\displaystyle{ H(S, j) = \sum^{m-1}_{i=0}\alpha^{m-(i+1)}\times char(s_{i+j}) }[/math][6][7] [math]\displaystyle{ H(S, j+1) = (H(S, j)-\alpha^{m-1}char(s_j))\cdot \alpha + s_{j+m} }[/math]
이는 j 번째 해시값을 알고 있다면, j+1 번째 해시값을 상수 시간 O(1) 연산만으로 계산할 수 있다는 것을 의미한다. 이 경우 전체 시간 복잡도는 아래와 같이 계산된다:
O(n): 각 부분 문자열에 대해 해시값 업데이트 O(m): 탐색할 패턴의 해시값 계산 총 O(n + m)
즉, Rabin-Karp 알고리즘은 Brute Force보다 훨씬 효율적인 문자열 검색 방법이다.
각주
- ↑ 이는 해시 테이블 자체의 크기를 제한하기도 한다.
- ↑ n은 키의 개수, m은 테이블의 크기를 의미한다.
- ↑ probing chain이 끊기기 때문이다.
- ↑ i는 k를 이진수로 표현하였을 때 필요한 비트의 수를 의미하며, 2i-1은 i개의 비트로 만들 수 있는 가장 큰 수에 해당한다.
- ↑ 주민등록번호의 경우에도 2020년 법 개정 이전에는 앞 여섯 자리는 성별과 출생 주소지 등에 대한 정보를 담고 있으므로 나쁜 해시 함수로 볼 수 있다.
- ↑ H(S, j)는 문자열 S의 j번째 위치에서 시작하는 길이 m의 부분 문자열의 해시값을 의미한다.
- ↑ [math]\displaystyle{ \alpha }[/math]는 보통 큰 수이며, 위치에 따라 가중치를 주는데 사용된다.