페이지 테이블

개요

컴퓨터 과학에서 페이지 테이블(page table)은 페이징 기법에서 사용되는 자료구조로서, 프로세스의 페이지 정보를 저장하고 있는 테이블이다. 하나의 프로세스는 하나의 페이지 테이블을 가진다. 테이블은 다음과 같이 색인과 내용으로 구성되어 있다.

• 색인 : 페이지 번호.
• 내용 : 해당 페이지에 할당된 물리 메모리(프레임)의 시작 주소. 이 시작 주소와 페이지 주소를 결합하여 물리 메모리 주소를 알 수 있다.

리눅스에서는 4단계 페이지 테이블을

PGD PUD PMD PTE (global direcotry / upper directory / mid-level directory / table entry)

로 구분한다.

Page Directory

각각의 페이지 테이블은, 전체내용을 모두 적기에는 주소 공간이 부족함으로 recursive하게 정리하여 페이지 테이블에 대한 크기를 줄였다. (모든 데이터를 저장한다면 크기는 오히려 page directory를 사용한 쪽이 조금 더 클 것이다, 그러나 그런 경우는 절대 없음으로 sparse하게 분포되는 경우 이 방식이 훨씬 데이터 크기를 적게 유지할 수 있다.) 이중 말단을 제외한 부분을 page direcotry라고 한다.

Page Table entry

page table에서 끝에 위치한 부분을 의미한다.

페이지 테이블 엔트리

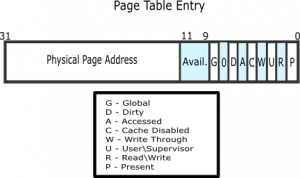
페이지 테이블 엔트리는 페이지 테이블에서 최하위에 위치한 실제 Physical memory를 가르치는 엔트리이다.

• S, Page Size: 하나의 페이지 엔트리가 가르키는 페이지 테이블 크기
• A, Accessed: 페이지가 읽히거나 써졌는지를 나타낸다. A비트는 CPU에서 의해서 정리되지 않고 OS의 특정한 목표로 인해서 clear된다.
• D, Dirty Flag: 페이지 테이블에 write이 있었는지
• C, Cached: 페이지 테이블을 TLB에 올려서 캐싱할것인지. (Page directory에서는 다른 비트)
• P, Present: 페이지가 존재하는지. 즉 Present란 현재 페이지가 Physical memory에 있다는 것을 나타낸다. 만약 swap-out되면 present는 clear되게 된다.
• R, Read/Write: R비트가 표시되어 있으면 read/write이 가능하며 아니면 read-only이다.
• U, User/Supervisor: U가 표시되어 있으면 CPL=3에서도 사용가능하나, 아니면 CPL=0에서만 사용가능하다.
• W, Write-Through: 페이지 교체 Policy를 Write-back 으로 할 것인가 아니면 Write-Back으로 할 것인가.
• G, Global: cr3 리셋에서 이 페이지를 TLB에서 제거하지 않는다.

Recursive Page Table

Recursive page table이란 페이지 테이블 말단에 자기자신을 향하는 주소를 할당하는 것을 말한다. 이 방식을 통해서 각각의 페이지 테이블에 대한 인덱스를 page table walking없이도 찾아 올 수 있다.