다른 명령
새 문서: 분류: Decision Making == 개요 == AI가 알고 있다고 가정하는 정보와, AI가 모른다고 가정하는 정보를 구분하여, 그 정보를 가지고 적절한 상황판단을 하는 것을 말한다. 이러한 상황에서 가장 좋은 판단을 어떻게 하는가를 구분하는 일을 한다. 예를 들어 리그오브레전드에서 전장의 안개가 있을 경우, AI가 그러한 정보를 이용하도록 하는 것이 중요하다. 이때 또한 중... |
편집 요약 없음 |
||
| 1번째 줄: | 1번째 줄: | ||
[[분류: | [[분류: 의사 결정]] | ||
== 개요 == | == 개요 == | ||
2023년 2월 24일 (금) 09:05 기준 최신판
개요
AI가 알고 있다고 가정하는 정보와, AI가 모른다고 가정하는 정보를 구분하여, 그 정보를 가지고 적절한 상황판단을 하는 것을 말한다. 이러한 상황에서 가장 좋은 판단을 어떻게 하는가를 구분하는 일을 한다. 예를 들어 리그오브레전드에서 전장의 안개가 있을 경우, AI가 그러한 정보를 이용하도록 하는 것이 중요하다. 이때 또한 중요한 것은 Phase를 조절하는 일이다. AI가 너무 사람을 괴롭히면 게임의 흥미가 떨어지게 된다. Player을 봐주기도 하고 실수를 하기도 하면서 Decision을 내려야 좋은 Fun을 제공할 수 있다. 결국 게임 AI의 최종 목표는 흥미의 전달이기 때문이다. 여기서 제시하는 방법은 즉각적인 피드백을 바탕으로 판단이 이루어지기 때문에 look ahead를 볼 수는 없다. 이러한 방법은 Adversarial search에서 제시한다.
방법
- Scripting: 제일 간단한 방법으로, 모든 상황에 대해서 일일이 다 기술하는 것을 말한다. 개발자 입장에서는 쉽고 빠르게 모든 상황에 대해서 처리할 수 있다는 장점이 있지만, 비개발자 입장에서는 이해하기 어렵다는 점과 모든 상황을 고려하는 점이 노동집약적이라는 점, 그리고 플레이어가 누군지 상관없이 똑같은 패턴의 작업만 반복한다는 한계가 존재한다.
- Finite State Machines: 유한 상태 머신을 이용한 방식으로, Scripting의 한계를 극복하기 위해서 그래픽 기반으로 desinger도 접근할 수 있도록 하는 것을 의미한다. 여러개의 상태를 기술하는 state들과 이러한 state들의 전이로 구성되어 작동한다. Switch문을 이용하여 쉽게 Scripting으로도 구현할 수 있다. 여기서 복잡도를 줄이기 위해서 FSM을 구조적으로, 즉 Hierarchical FSM을 이용하여 기술할 수 있다.
- Decision Trees: 기본적으로 If-else문을 이용하여 코딩을 하는 것을 생각하면된다. 예를들어서 특정한 조건이 true이면 공격하고 false이면 수비하는 것을 들 수 있다. FSM은 Decisino Tree와 기본적으로 서로 치환 가능하다.
Behavior Tree
Tasks
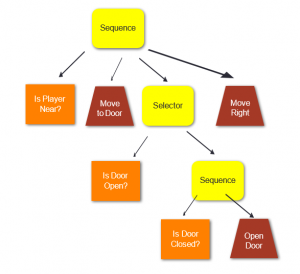
- Action: Action task 는 실제 행동을 표현하는 단말 노드이다. 항상 true 나 false 를 반환하게 되어 있다.
- Condition: 조건을 따지는 단말 노드이다. 참이면 true 거짓이면 false를 리턴한다.
- Composite: 중간에 위치하는 노드로써, Action이나 Condition노드 혹은 다른 Composite노드를 자식으로 두면서 특정한 기능을 수행한다.
- Sequence: 노드들을 왼쪽에서 오른쪽으로 차례대로 실행시키면서, 하나라도 실패하면 fail을 리턴하고 현재 실행을 종료한다. 그러나 모든 노드가 성공하면 success를 리턴하고 다음 Task로 이동한다.
- Selector: Fallback Task라고도 불리며, 노드들을 왼쪽에서 오른쪽으로 차례대로 실행시키면서, 하나라도 성공하면 거기서 멈추고 return true를 한다. 모두 실패하면 return false를 한다.
- 기타: RandomSelector.. RandomSequence.. Parallel..등 Sequence는 Task Node들을 어떻게 실행시키냐에 따라서 여러 종류가 올 수 있다.
- Decorators: 자식 노드에 특별한 역활을 할 수 있도록 도와준다. Repeat, UntilFail, Filter, Inverter, Semaphore등이 있다.
중요한 점은 Composite 노드들 (Sequence, Selector)노드는 항상 중간에 Action Condition Node는 말단에 위치해야 한다는 점이다.
구현
모든 노드들은 Task를 상속하여 이루어진다. Task들은 return값으로 SUCCESS혹은 FAIL을 상황에 따라서 리턴하게 된다. Composite는 Task를 상속한다. 이때 Composite는 중간노드이기 때문에, 자식 노드들을 List형태로 저장하게 된다. Sequences나 Selector와 같은 경우는 Composite을 상속하게 된다. 상속받은 Composite중간 노드들은 List에 저장된 Task들을 run하고 결과에 따라서 SUCCESS혹은 FAILURE을 리턴하면 된다. 이때 Sequence와 같은 노드들은 별도의 thread로 넣거나, 한 프레임에 한 노드만 작동하게하는등 제약을 주어야 노드들의 계산에 의한 시간으로 게임이 block되는 것을 막을 수 있다.
Task가 Player의 정보와 같은 Data에 접근하기 위해서 blackboard와 같은 것을 사용할 수 있다. blackboard란 공유 메모리에 원하는 정보를 작성해 놓고 필요한 노드가 정보를 얻는 것을 말한다. 예를 들어서, 플레이어가 가까울 경우 접근하는 Sequence는 Move to player가 Is player Near에서 얻은 정보를 바탕으로 움직여야 될 것이다.
Autonomous AI
AI가 스스로 전략을 결정하여 행동하는 것을 말한다. FSM, Decision Tree와 같은 Hardcode된 전략을 따르는 것이 아니라 AI가 Decision을 스스로 만들어 내게 된다. 최근에 강화학습을 이용해서 만들어 내는 AI들은 Autonomous하다고 할 수 있다.
Decision Theory
상황이 주어진경우 다음상태를 봤을때 가장 좋아보이는 Action을 도출하는 것을 말한다. 좋고 나쁨을 나타내는 함수 (Utility Fuction) U(X)를 정의할 수있다. 이 함수의 입력은 State이며 출력은 Action이다. 이러한 U함수는 미리 정의해 두어야 한다. 예를 들어 체스에서 U(X)는 X는 체스판위의 말들의 위치가 될 것이고, U(X)는 말들의 점수의 차라고 할 수 있을 것이다.
더 예를 들자면 RTS게임에서 Utility함수는 다음과 같이 정의 될 수 있다.
- [math]\displaystyle{ U(s)=\sum_t w_t({c_t}^{friendly} - {c_t}^{enemy}) }[/math]
여기서 t는 유닛의 종류, w는 유닛의 중요도에 따른 가중치, c는 유닛의 개수가 될 수 있다. 물론 여기에 여러 변수를 더해서 좀더 복잡하지만 정확하게 만들 수도 있다.
여기에 더해서 Action을 a로 하고 State를 s라고 할때, Result(s,a)를 정의할 수 있다. Result(s,a)는 action과 state에 따라서 계산된 다음 State를 계산하는 함수이다. 이때 우리는 S에 대한 모든 정보를 알 수 없기 때문에, Result(s,a)는 어디까지나 확률로 나온다. 예를 들어서 내가 부쉬에 들어가서 킬각을 노릴때 다음결과과 갱을 당할지 아니면 성공적으로 딜교를 할지는 모르는 것이기 때문에 조건부 확률로 나오게 되는 것이다. 여기서 s'은 예상되는 다음결과이며, e는 내가 아는 s에 대한 정보이다.
- [math]\displaystyle{ P(Result(s,a)=s' | e) }[/math]
최종적으로 내가 e(estimated current state)가 주어진 경우 Action a를 할 경우 생기는 최종적인 U값은 다음과 같이 정의된다.
- [math]\displaystyle{ \sum_{s'} P(Result(a,s) = s'|e)U(s') }[/math]
여기서 체스와 같은 퍼즐게임은 Result와 U가 쉽게 정의된다. 그러나 RTS게임과 같은 경우 정의하는 것이 매우 복잡하기 때문에 단순히 정의할 수 없다. 따라서 RTS와 같은 경우 Simulation을 통해서 학습을 통해 위에 있는 함수를 정의하게 된다.
계산에, Utility함수와 가능한 Action의 리스트 그리고 Result를 계산하기 위한 Simulation하는 함수가 필요하다. 이러한 3개의 함수를 바탕으로 Action이 이루어지기 전에 game에서 요구되는 Effect를 계산하고 가장큰 U를 가지는 Action을 취하는 것이다. 시물레이션이 Stochastic한 경우아 Deterministic한 경우로 나뉜다. Stochastic한 경우는 시간이 허락하는 범위내에서 여러번 시물레이션 하고 평균적으로 어떤일이 이루어지는지 알아낸뒤 그 평균값을 이용하면 된다. 이는 몬테 카를로 법칙에 의하여 최적의 값을 도출하는 것이 알려져 있다.
현재 상황에서 Action의 유틸리티에 대해서 상태를 따지지 않고, Utility를 정의하는 방식도 있다. 이러한 방식은 Result함수를 정의하지 않고도 U값을 따질 수 있게 해준다. 한 예를 보자면, 심즈에서 Utility를 두 단계로 나누어서 계산하는 방식을 들 수 있다. 행동에대한 Motivation단계와 Action단계를 나누어서 Motivation을 충족시키기 위해 필요한 Action들만 고려해 주는 것이다.
이때 정보의 중요성또한 고려될 수 있다. 이러한 Value of Information은 다음과 같이 정의된다. 내가 알려고 하는 정보들이 여러가지 것들중에 하나일때, 내가 그러한 정보를 얻을 경우 생기는 효용성을 계산하는 것을 말한다. 예를들면, 내가 상대방 부쉬에 들어가는 것을 계산할 수있다. 첫번째 가능성으로는 정글이 부쉬에서 기다리고 있을 수도 있다. 이러한 경우 나는 죽는 것이 패널티로 부과된다. 두번째는 부쉬에 아무도 없는 경우를 들 수 있다. 이러한 경우 와드를 박는 다는 것은 미지의 정보(부쉬에 정글이 있는 확률)에 대한 이득을 따져서 결정되게 된다. 즉 VPI는 정보를 알때의 예측값과 정보를 모를때의 예측의 차이로 계산된다.
- [math]\displaystyle{ VPI_e(E) = \sum_k P(E = e_k)EU(a_k^*|e, E=e_k) - EU(a^*|e) }[/math]
이를 통해서 얻게 되는 VPI는 정보를 얻게 됨으로써 얻게 되는 이득이다. 이때 내가 저 정보를 얻기 위해서 드는 노력은 저 값보다는 작아야 한다. 그래야 그 것이 이득이 된다. 결국 와드값 75원보다 갱 회피가 더 큰 이득이면 와드를 사야하는 것이다. 이래서 프로게이머들이 항상 와드를 사는 것을 알 수 있다.
