개요
카메라의 위치와 원점을 잡는 과정이다. 좌표공간의 카메라는 3개의 변수들을 가진다. 위치, 카메라의 시선의 방향, 그리고 카메라의 위쪽 방향. 쉽게 설명하자면 어떤 사물을 바라보는 사람의 머리는 위치, 사물로의 방향, 정수리의 방향으로 나타내는 것을 말한다. 이러한 변수들은 유저가 입력하게 되고, 월드 좌표계에서 할당된다.
수식
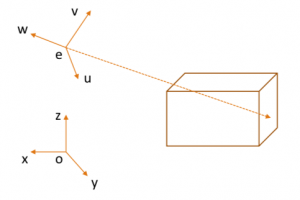
카메라의 위치를 [math]e=(x_e,y_e,z_e) [/math]
카메라가 향하는 방향을 [math]g=(x_g,y_g,z_g) [/math]
카메라의 위쪽 방향을 (정수리 방향) [math]t=(x_t,y_t,z_t) [/math] 라 정의하자
이때 이런 값들은 사용자가 입력하는 것이다. (예를 들어 사용자가 마우스로 고개를 돌린 상황) 또한 이러한 값들은 월드 좌표계에서 정의된다.
왜냐하면 Viewing Transformation은 월드 좌표계에서 카메라 좌표계로 옮기는 좌표계이기 때문이다. 이제 할 일은 카메라를 중심으로 하는 새로운 기저 벡터들을 설정하는 것이다. 기저 벡터를 잡는 다는 것은 쉽게 생각해서 카메라를 중심으로하는 새로운 좌표축들을 설정한다고 생각하면 된다. 그래야 이 좌표축들을 중심으로 사물들의 위치를 나타낼 수 있다.
이제 우리는
[math]w=-\frac{g}{\lVert g \rVert}[/math]
[math]u=\frac{t*w}{\lVert t*w \rVert}[/math]
[math]v=w*u[/math]
로 새로운 좌표축을 세울 수 있다. 당연히 세 기저 벡터들은 서로 수직이며 새로운 좌표축을 정의한다.
행렬
Homogeneous Matrix를 통해서 나타내면 다음과 같다.
첫번째로 카메라 위치 e를 월드좌표계의 원점으로 이동시킨다
다음으로 u, v, w를 x, y, z와 정렬되도록 변환한다. 변환 행렬 역행렬참고 (orthogonal 형렬의 역행렬은 transpose 행렬과 같다.)
[math] M_{view} = \begin{bmatrix} u & v & w & e \\ 0 & 0 & 0 & 0 \end{bmatrix}^{-1} = \begin{bmatrix} x_u & y_u & z_u & 0 \\ x_v & y_v & z_v & 0 \\x_w & y_w & z_w & 0 \\0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -x_e \\0 & 1 & 0 & -y_e \\0 & 0 & 1 &-z_e \\0 & 0 & 0 & 1 \end{bmatrix} [/math]