Time-bounded A*

개요

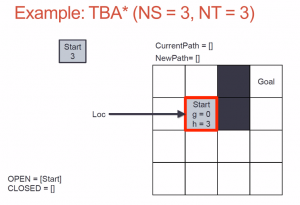
A*는 목적지까지의 경로를 찾아야만, 탐색이 종료된다. 실시간 게임에서 이러한 과정을 기다리기는 너무 오래 결릴 수도 있음으로, 경로 탐색이 끝나기 전에 납득할 만한 경로를 주는 알고리즘이 TBA* (Time-Bounded A*)이다.

Real-time이며 Optimal하다.

알고리즘

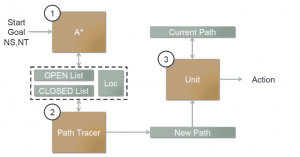
A*알고리즘을 이용하면서 경로를 만든다. 그러나 경로를 만들던 도중에 현재 생각되는 최선의 위치라고 생각되는 Path를 탐색하고 움직임에 반영시킨다. 그러면서 한정된 자원 (NS _ 탐색할 수 있는 노드의 개수, NT - 탐색할 수 있는 경로의 깊이)를 이용하여 Path를 계속 추적하고 현재 AI가 움직이는 Path와 새로운 Path가 겹치는 지점이 있으면, 새로운 패스를 반영하고 아니면 현재 패스를 백트래킹시킨다. 그 외의 경우에는 현재 패스를 따라가게 된다. 여기서 NS와 NT는 컴퓨터 속도에 따라서 자유롭게 설정 가능하다.

결국 기본적으로는 A*와 같지만, 중간에 산출되는 결과물을 AI가 이용할 수 있도록 추가하는 과정이 있는 알고리즘이다.

우선 기본적인 a*알고리즘을 이용해서 ns개의 노드만큼 경로를 탐색한다. Path Tracer는 closed된 노드중에 h값이 제일 작은 nt개의 path를 만든다. 여기서 한턴에 신장할 수 있는 최대 path의 길이는 nt개로 제한된다. 이 작업을 계속 반복하면된다.

Pseudocode

function reconstruct_path(cameFrom, current)
    total_path := {current}
    while current in cameFrom.Keys:
        current := cameFrom[current]
        total_path.prepend(current)
    return total_path

// A* finds a path from start to goal.
// h is the heuristic function. h(n) estimates the cost to reach goal from node n.
function A_Star(start, goal, h)
    // The set of discovered nodes that may need to be (re-)expanded.
    // Initially, only the start node is known.
    // This is usually implemented as a min-heap or priority queue rather than a hash-set.
    openSet := {start}

    // For node n, cameFrom[n] is the node immediately preceding it on the cheapest path from start
    // to n currently known.
    cameFrom := an empty map

    // For node n, gScore[n] is the cost of the cheapest path from start to n currently known.
    gScore := map with default value of Infinity
    gScore[start] := 0

    // For node n, fScore[n] := gScore[n] + h(n). fScore[n] represents our current best guess as to
    // how short a path from start to finish can be if it goes through n.
    fScore := map with default value of Infinity
    fScore[start] := h(start)

    while openSet is not empty
        // This operation can occur in O(1) time if openSet is a min-heap or a priority queue
        current := the node in openSet having the lowest fScore[] value
        if current = goal
            return reconstruct_path(cameFrom, current)

        openSet.Remove(current)
        for each neighbor of current
            // d(current,neighbor) is the weight of the edge from current to neighbor
            // tentative_gScore is the distance from start to the neighbor through current
            tentative_gScore := gScore[current] + d(current, neighbor)
            if tentative_gScore < gScore[neighbor]
                // This path to neighbor is better than any previous one. Record it!
                cameFrom[neighbor] := current
                gScore[neighbor] := tentative_gScore
                fScore[neighbor] := gScore[neighbor] + h(neighbor)
                if neighbor not in openSet
                    openSet.add(neighbor)

    // Open set is empty but goal was never reached
    return failure