상위 문서: Data Structures
개요
해당 문서에서는 알고리즘등에서 많이 응용되는 우선순위 큐(priority queue)에 대해 설명한다. 우선순위 큐는 FIFO 원칙을 따르는 일반적인 queue와는 달리, 우선순위 큐는 각 원소에 우선순위를 부여하고, 우선순위가 가장 높은 우선순위 원소가 먼저 처리되는 자료구조이다. 즉 단순 정렬과 다르게, 새로운 작업이 들어올 때마다 전체를 다시 정렬하지 않고 효율적으로 관리할 수 있는 구조를 제공한다.
데이터를 한 번 정렬해 놓으면, “가장 작은 값”이나 “가장 큰 값”을 바로 알 수 있다. 하지만 이러한 방식으로 가장 중요한 원소를 찾는 것은 새로운 데이터가 들어올 때마다 번거롭게 전체를 다시 정렬해야 한다는 문제가 있다.(O(n log(n)) 시간) 하지만 우선순위 큐는 가장 중요한(작은/큰) 원소만 빠르게 찾을 수 잇게 설계된 자료구조이므로, 정렬을 유지할 필요가 없다. 새로운 데이터가 들어오면 그냥 힙에 삽입하면 되고, 이는 O(log n)만 걸린다.
Priority Queue Operations
아래는 우선순위 큐에서 지원하는 기본적인 연산 3가지이다:
- Insert(Q, x): 새로운 원소 x를 우선순위 큐 Q에 삽입한다.
- 원소는 보통 (key, value) 형태로 들어오며, key가 우선순위를 나타낸다.
- 시간 복잡도는 O(log n)이다. (힙에서 삽입 시 트리 높이만큼 조정 필요)
- Find-Minimum(Q) / Find-Maximum(Q): 큐 안에서 가장 작은 key(또는 가장 큰 key)를 가진 원소를 반환한다.
- 최소 힙(min-heap)이라면 Find-Minimum은 O(1)로 가능.
- 최대 힙(max-heap)이라면 Find-Maximum은 O(1)로 가능.
- 시간 복잡도는 O(log n)이다. (루트 제거 후 재정렬 필요)
- Delete-Minimum(Q) / Delete-Maximum(Q): 가장 작은 key(혹은 큰 key)를 가진 원소를 큐에서 제거한다.
- 시간 복잡도는 O(1)이다. (힙의 루트 확인만 하면 됨)
Heap
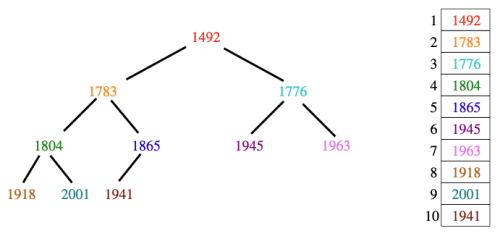
힙(Heap)은 완전 이진트리(complete binary tree) 기반의 자료구조이다. 즉, 모든 레벨이 다 채워져 있고, 마지막 레벨만 예외적으로 왼쪽부터 채워지는 트리를 기반으로 한다. 힙 자료 구조는 아래와 같은 조건을 만족해야 한다.
- 리프(leaf)노드는 마지막 두 층에서만 리프가 분포할 수 있다.
- 마지막 레벨은 노드 들이 왼쪽부터 순서대로 채워지고, 그 위 레벨들은 전부 채워져야 한다.
- 루트의 키는 자식들의 키보다 작거나 같아야 하며(min heap의 경우), 모든 서브트리도 다시 힙 구조여야 한다.
조건 1, 2는 트리의 형태(shape) 를, 조건 3은 순서 규칙(ordering) 을 규정한다. Figure 1은 각각 트리 구조와 배열 인덱스를 통해 표현한 힙 자료구조의 예시이다. 힙은 이러한 조건을 통해서 partial order를 유지한다. 이는 전체를 정렬하지 않아도 최솟값/최댓값을 빠르게 식별 가능하게 한다.
Array-Based Heaps
일반적으로 트리는 각 노드가 자식 포인터를 가지지만, 힙은 배열 기반 표현이 더 자연스럽다. 배열 인덱스를 통해 binary tree를 나타내기 위해서는 아래와 같은 규칙을 가지면 된다:
- 노드 k의 왼쪽 자식: 2k
- 오른쪽 자식: 2k+1
- 부모: ⌊k/2⌋
- heap의 루트 노드의 인덱스는 "1"
이때 트리가 희소(sparse) 하면 비효율적이다. 예를 들어, 높이 h를 가지는 트리에 대해 [math]\displaystyle{ n \lt 2^h }[/math]일 때, 존재하지 않는 내부 노드도 배열 공간을 차지한다. 따라서 트리가 perfect balanced tree라는 것은 주어진 노드 수에 대해 높이 h가 최소라는 것을 의미하므로, 주어진 노드 수에 대해 배열을 최대한 활용할 수 있다. 또한 배열 기반의 표현은 포인터 기반 트리보다 수정 유연성이 떨어진다.
Implementing Heap
해당 문단에서는 힙의 삽입과 삭제를 하는 코드와, 이를 구현하기 위한 다른 코드들에 대해서 살펴본다. 이때 해당 문단은 min heap의 구현을 기준으로 살펴본다.
Constructing Heaps
Heap은 한번에 모든 원소들을 삽입하는 것이 아니라, 한번에 하나씩 트리에 원소들을 삽입하며 점진적(heapify by insertion)으로 생성한다. 이를 위해서 배열의 가장 왼쪽 빈 칸에 새 원소를 삽입하고, 부모보다 작으면 이를 swap(bubble-up)하는 방식이다. 이때 perfect balanced tree는 힙의 높이 h가 n개의 노드가 있을 때, h = ⌊log n⌋여야 한다. 이에 따라 시간 복잡도는 각각의 원소 삽입에 대한 시간 복잡도는 O(log(n))이며, 전체 n개의 노드에 대한 시간 복잡도는 O(n log(n))이다. 이를 구현하기 위한 코드는 아래와 같다:
void pq_insert(priority_queue *q, item_type x) {
if (q->n >= PQ_SIZE) { //PQ_SIZE는 배열이 저장할 수 있는 노드의 최대 크기
printf("Warning: priority queue overflow!\n");
} else {
q->n = q->n + 1; //원소를 마지막 위치에 배치
q->q[q->n] = x;
bubble_up(q, q->n); //적절한 위치에 도달할 때 까지 swap
}
}
해당 코드는 큐가 가득 차면 overflow를 경고한다. 그렇지 않으면 원소를 마지막 위치에 넣고, bubble_up으로 힙 조건을 유지한다. bubble_up 코드는 아래와 같이 구현된다.
void bubble_up(priority_queue *q, int p) {
if (pq_parent(p) == -1) return; // 루트 도달, 더 이상 부모 없음
if (q->q[pq_parent(p)] > q->q[p]) { //부모가 자식보다 값이 크면 스왑
pq_swap(q, p, pq_parent(p));
bubble_up(q, pq_parent(p)); //재귀적으로 배치
}
}
해당 bubble up 코드는 배열로 구현된 heap의 마지막에 삽입된 원소를 부모와 비교하며, 해당 원소를 재귀적으로 위로 올리는 방식이다.
Extracting the Minimum Element
Min heap의 구현에서 필수적인 코드 중 하나는 루트의 값(최솟값)을 꺼내고, 마지막 원소를 루트로 가져온 뒤 bubble_down으로 재정렬하는 것이다. 이는 아래와 같이 구현된다:
item_type extract_min(priority_queue *q) {
int min = -1;
if (q->n <= 0) {
printf("Warning: empty priority queue.\n");
} else {
min = q->q[1]; // 루트 값
q->q[1] = q->q[q->n]; // 마지막 원소를 루트에 배치한다.
q->n = q->n - 1;
bubble_down(q, 1); // 이를 밑으로 bubble_down하면서 heap 조건을 복구한다.
}
return min;
}
아래는 이를 구현할 때 사용하는 bubble_down 함수를 구현하는 코드이다:
void bubble_down(priority_queue *q, int p) {
int c = pq_young_child(p); //자식 노드의 인덱스(c = 2p)
int min_index = p; //min_index는 p, 2p, 2p+1 중에서 가장 작은 원소의 인덱스 추적
for (int i = 0; i <= 1; i++) { // 왼쪽(i=0), 오른쪽(i=1) 자식 검사
if ((c + i) <= q->n) { // 자식 인덱스가 힙 크기 범위 안이면
if (q->q[min_index] > q->q[c + i]) {
min_index = c + i; // 더 작은 자식을 찾으면 갱신
}
}
}
if (min_index != p) {
pq_swap(q, p, min_index); // p와 q를 swap
bubble_down(q, min_index); // 재귀적으로 수행
}
}
Faster Way to Build a Heap
힙을 한 원소씩 insert + bubble_up을 통해 점진적으로 생성하면 O(n log(n))의 시간 복잡도가 소요된다. 하지만 아래와 같은 heapify를 이용하면 더 빠르게 O(n)에 힙을 만들 수 있다.
void make_heap_fast(priority_queue *q, item_type s[], int n) {
int i;
q->n = n;
for (i = 0; i < n; i++) {
q->q[i + 1] = s[i]; // 배열을 힙에 그대로 복사
}
for (i = q->n/2; i >= 1; i--) {
bubble_down(q, i); // 자식이 있는 모든 노드에 대해 bubble_down 수행
}
}
이는 배열 s[]를 통째로 복사 후, 내부 노드(leaf 아님)부터 거꾸로 bubble_down 실행하는 방식이다. 해당 알고리즘의 시간 복잡도는 아래와 같이 계산할 수 있다:
- 높이가 h인 노드는 최대 [math]\displaystyle{ \lceil\frac{n}{2^{h+1}}\rceil }[/math]개 존재
- 높이가 h인 각 노드의 bubble_down 비용은 [math]\displaystyle{ O(h) = O(log(n)) }[/math]
[math]\displaystyle{ \therefore\,\, O(\sum^{log(n)}_{h=0}\frac{n}{2^{h+1}}\cdot h) = O(n \sum^{log(n)}_{h=0}\frac{h}{2^{h}}) }[/math]
이제 우리가 해야하는 것은 위 시간복잡도가 O(n)으로 수렴한다는 것을 보이는 것이다. 이는 아래와 같다:
- 기하급수(geometric series): [math]\displaystyle{ \sum^{\infty}_{k=0}x^k=\frac{1}{1-x}, |x|\lt 1 }[/math]
- 양변을 미분: [math]\displaystyle{ \sum^{\infty}_{k=0}kx^{k-1}=\frac{1}{(1-x)^2} }[/math]
- [math]\displaystyle{ x }[/math]를 양변에 곱하면: [math]\displaystyle{ \sum^{\infty}_{k=0}kx^{k}=\frac{x}{(1-x)^2} }[/math]
- [math]\displaystyle{ x = 1/2 }[/math]를 대입하면: [math]\displaystyle{ \sum^{\infty}_{k=0}k(1/2)^{k}=2 }[/math]
따라서 [math]\displaystyle{ O(n \sum^{log(n)}_{h=0}\frac{h}{2^{h}}) }[/math]는 h가 양의 방향으로 발산할 때, [math]\displaystyle{ O(2n) = O(n) }[/math]으로 수렴한다.
Applications of Priority Queues
사실은 일반적인 stack(LIFO)이나 queue(FIFO)도 사실은 특수한 형태의 우선순위 큐이다. stack은 가장 최근에 들어온 원소가 우선순위가 높고, queue는 가장 먼저 들어온 원소가 우선순위가 높은 것이다.
우선순위 큐는 시뮬레이션(simulation) 에서 매우 자주 활용된다. 시뮬레이션은 시간의 흐름에 따라 사건(event)이 발생하는데, 각 사건의 발생 시간이 다르다. 이때 우선순위 큐를 이용하면 “가장 빨리 일어날 사건(최소 시간)”을 효율적으로 뽑아낼 수 있다. 예를 들면 공항에서 다음 비행기 착륙, 주차장에서 다음 차량 입출차 등이 있다.
또한 heap은 그 특성 덕에 정렬 알고리즘에 응용되어 heap sort 알고리즘을 만드는데 쓰인다. 자세한 내용은 heap sort 문서를 참조해 주십시오.
