개요
Discriminative model을 사용한 분류기중 가장 널리 사용되는 방식이다. Logistic Regression은 각각의 샘플들이 특정한 class에 분류될 확율을 Regression시킨다. Logistic Regression 은 Logistic fuction을 이용하여 class들을 분류한다. Logistic Regression 은 선형분류의 한예라고도 할 수있다.
Logistic Function
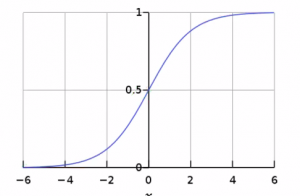
여기서 L은 커브의 높이(대부분 1로 주어짐), x_0는 중간값 (여기서는 0으로 주어짐), K는 함수의 기울기를 의미한다.
- [math]f(x)=\frac{L}{1 + e^{-k(x-x_0)}}[/math]
현대의 Deep Neural Networks들은 cross entropy를 loss function으로 사용한다.
- [math]J(w)=-\frac{1}{N} \sum[y_nlog\hat{y}_n + (1-y_n)log(1-\hat{y}_n)][/math]
이경우 Logistic Regression loss function은 다음과 같다.
특징
- 결과 값이 확률값처럼 0과 1사이에서 정의된다.
- 미분값이 전 구간에서 정의되어서 전 구간에서 연속이다.
- Mirror symmetric성질을 가진다. 이는 중심점에대해서 점대칭인 특징을 가지는 것을 의미한다.
- 미분을 계산하기 매우 편리하다. 이는 미분할 필요도 없이 다음과 같은 공식으로 주어진다. [math]S'(x)=S(x)(1-S(x))[/math]
Logistic Regression
로지스틱 함수는 0과 1 사이의 값을 가진다. 이는 Logistic함수를 확률을 나타내기 위해서 사용할 수 있다는 말과 같다. 즉 Logistic Regression은 조건부 확률 P(X|Y)를 Logistic function으로 나타내어서 classfication을 한다.
Binary Classification
바이너리 케이스인경우 경우가 두가지만 나옴으로 치환을 통해서 p(x)로 나타낼수 있다. 이런 경우 식은 다음과 같이 정리된다.
- [math]p\left( x \right) \gt 1-p\left( x \right) \\ \frac { p\left( x \right) }{ 1-p\left( x \right) } \gt 1\\ \log { \frac { p\left( x \right) }{ 1-p\left( x \right) } } \gt 0 \\ \\ { \overrightarrow { \beta } }^{ T }\overrightarrow { x } \gt 0[/math]
파라미터의 학습
[math]w_o[/math]는 특별히 bias로 불리운다. 만약 feature가 d개의 dimension을 가지면, [math]w_o, w_1, ... , w_{d-1}[/math] 로 파라미터를 나타낼 수 있다.