개요

가장 먼저 개발된 일루미네이션 방식으로써, 물체의 표면의 색을 ambient, diffuse, specular 로 나누어서 계산하는 방식이다. 각각 물체의 전반적인 색, 깊이에 따라 달라지는 색, 반사광을 담당한다. 물체의 색을 매우 휴리스틱한 방식으로 처리하며, 결과는 오래된 기술 답게 빠르지만 지금의 시점으로써는 안좋은 결과를 가져온다.
전체 수식
ambient, diffuse, specular 를 각 빛마다 모두 더해서 구하게 된다.
- [math]\displaystyle{ I_{total} = \sum_{i=1}^{number of lights}L_a^iK_a+L_d^iK_dmax(0,n*l^i)+L_s^iK_smax(0,r^i*v)^s }[/math]
Ambient
모든 면이 같은 양의 빛 에너지를 받는다는 가정하에 처리하는 항이다. 표면의 위치나 방향, 관찰자의 방향, 빛의 방향같은 것은 모조리 무시한다.
- [math]\displaystyle{ I=L_a*K_a }[/math] (L_a:빛의 강도, K_a:ambient 항의 계수)
Diffuse
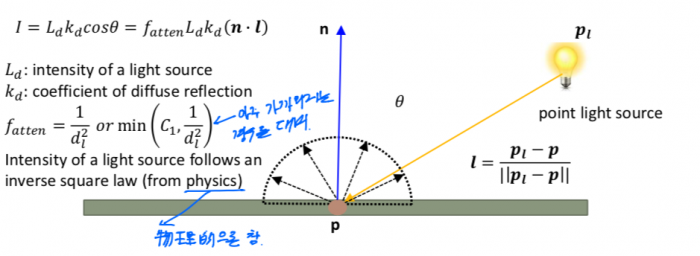
빛이 이상적인 diffuse 표면과 만났을 경우 (Lambertian), 반사되는 정도를 계산한다. 이때 반사되는 빛의 양은 표면의 노말 벡터와 빛의 방향 오로지 두개에 의해서 영향을 받는다는 가정하에 계산하게 된다. 만약 diffuse 계수가 1보다 크면 빛이 오히려 다 많이 나오는 경우도 생긴다. 즉 diffuse 계수는 1보다는 작아야 한다.
- [math]\displaystyle{ I = f_{atten}L_dK_d\cos\theta }[/math]
- [math]\displaystyle{ \cos\theta = n*l }[/math] (만약 n 과 l 이 unit 벡터이면 성립한다. (내적의 성질))
- [math]\displaystyle{ f_{atten} = \frac{1}{d^2} }[/math]
Specular Reflection
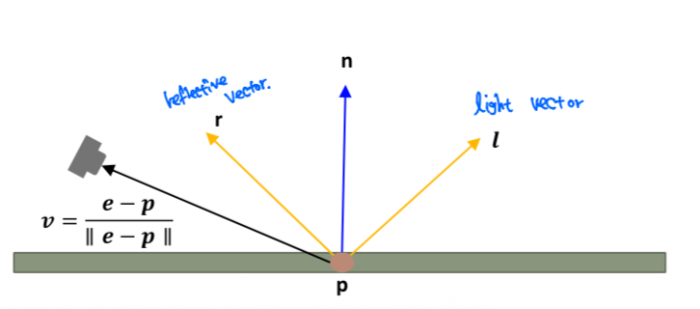
빛이 빛나는 불체와 만날경우 생기는 하이라이트를 계산하기 위해서 더해준다. 빛이 보는 방향과 shiness 를 변수로 하여 계산한다. snell의 법칙에 따르면 이상적인 표면에서 빛은 들어온 각도와 정확히 같은 각도로 반사된다. ([math]\displaystyle{ n_i=n_o }[/math]임으로)
- [math]\displaystyle{ I = L_sK_s\cos^s\alpha=L_sK_s(r*v)^s }[/math] s 는 shiness (빛나는 정도)
- [math]\displaystyle{ r=2(n*l)n-l }[/math] 이 식이 이미하는 것은 그림과 같이 n에 대해서 같은 정 반대에 있는 l을 작도한 것이다.
Blinn-Phong
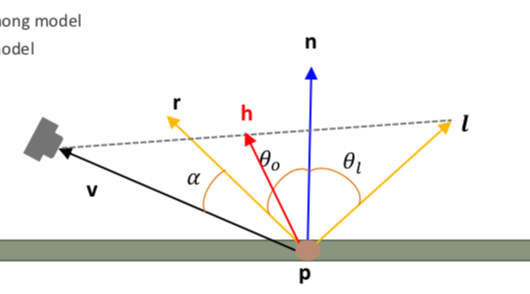
퐁 specular 을 보다 더 빠르게 하기위해서 정확한 r을 계산하는 것이 아니라 근삿값 h를 계산하는 방식이다. 현재 아무도 정말 아무도 사용하지 않는 방식이다.
- [math]\displaystyle{ h=\frac{l+v}{\lVert l + v \rVert} }[/math]
- [math]\displaystyle{ I=L_sK_s(n*h)^s }[/math]
