Edit Distance

youngwiki

상위 문서: Dynamic Programming

개요

문자열을 비교할 때는 오탈자가 있는 문자열을 고려해야 하는 경우가 있으며, 이를 위해서 근사(approximate) 매칭이 필요하다. 이를 위해서 두 문자열이 얼마나 다른지를 측정하는 척도가 필요하며, 이를 Edit Distance라고 한다. 이는 문자열 A를 문자열 B로 바꾸기 위해 필요한 최소 변경 횟수에 해당한다. Edit Distance는 보통 세 가지 연산을 기반으로 한다:

  1. Substitution (치환): 한 글자를 다른 글자로 바꾸기[1]
  2. Insertion (삽입): 문자 하나를 새로 삽입[2]
  3. Deletion (삭제): 문자 하나 삭제[3]

Simple Recursive Algorithm

Edit Distance 계산은 문자열 뒤에서부터 비교하면서 재귀적으로 해결할 수 있다. 이는 두 문자열 두 문자열 S[1..i], T[1..j]이 있을때 마지막 문자를 비교하여 해결할 수 있다. 만약 비교하는 두 문자가 같으면 비용 증가 없이 이전 문제로 이동한다.[4] 반면 두 문자가 다른 경우에는 substitution을 통해 Edit Distance를 1 증가시킨다.[5]

Recurrence Relation

위에서 설명한 원리를 점화식으로 풀면 아래와 같다: 

D[i,j] is minimum of:
• D[i−1,j−1] if S[i]=T[j]: 둘이 같으면 비용 추가 안 됨
• D[i−1,j−1]+1 if S[i]≠T[j]: 둘이 다르면 substitution 필요
• D[i,j−1]+1 for an insertion into S: T에서 문자를 하나 가져오는 경우(insertion)
• D[i−1,j]+1 for a deletion from S: S에서 문자를 하나 버리는 경우(deletion)

Recursive Edit Distance Code

아래는 단순 재귀 기반의 알고리즘을 C 코드로 옮긴 예시이다: 

#define MATCH   0      /* enumerated type symbol for match */
#define INSERT  1      /* enumerated type symbol for insert */
#define DELETE  2      /* enumerated type symbol for delete */

int string_compare_r(char *s, char *t, int i, int j) {
    int k;             /* counter */
    int opt[3];        /* cost of the three options */
    int lowest_cost;   /* lowest cost */

    if (i == 0) {      /* indel is the cost of an insertion or deletion */
        return (j * indel(' '));
    }

    if (j == 0) {
        return (i * indel(' '));
    }

    /* match is the cost of a match/substitution */

    opt[MATCH]  = string_compare_r(s, t, i-1, j-1) + match(s[i], t[j]);
    opt[INSERT] = string_compare_r(s, t, i,   j-1) + indel(t[j]);
    opt[DELETE] = string_compare_r(s, t, i-1, j  ) + indel(s[i]);

    lowest_cost = opt[MATCH];

    for (k = INSERT; k <= DELETE; k++) {
        if (opt[k] < lowest_cost) {
            lowest_cost = opt[k];
        }
    }

    return (lowest_cost);
}

Recursive Algorithm Using DP

위에서 구현한 단순한 재귀 알고리즘은 같은 (i, j) 상태를 수백 번, 수천 번 다시 계산한다. 이때 전체 가능한 상태의 수는 |S|×|T| 뿐인데, 이를 매번 재계산하기 때문에 비효율적이다. 실제로, 단순 재귀 알고리즘을 실제로 구현할 경우 시간 복잡도는 무려 O(3m+n)이다.

이를 단축시키기 위해 (i, j)를 계산한 값을 테이블에 저장하고, 이를 다시 사용하여 시간을 단축시킬 수 있다. 이는 동적 프로그래밍(DP)을 활용하여 구현될 수 있다. 이를 구현하기 위한 DP 테이블은 2D 배열 m[i][j]으로 구성된다. 테이블의 각 칸에는 그 위치까지 컴퓨팅한 최소 비용(cost)과, 어떤 연산(MATCH/INSERT/DELETE)으로 이 칸에 왔는지 추적하기 위한 포인터(parent)가 저장된다. 이때 parent는 실제 편집 경로(edit sequence)를 복원하는 데에 사용된다. 아래는 해당 자료구조를 C언어 코드로 구현한 예시이다: 

typedef struct { 
    int cost;               /* cost of reaching this cell */
    int parent;             /* parent cell */
} cell;

cell m[MAXLEN+1][MAXLEN+1]; /* dynamic programming table */

이때 DP 테이블의 각 칸은 vertex처럼 간주할 수 있으며, (i, j) → (i+1, j), (i, j+1), (i+1, j+1) 방향으로 edge가 존재한다고 할 수 있다. 즉, 이렇게 간주하면 DAG(Directed Acyclic Graph)이므로 topological order(위상 정렬)로 평가할 수 있다. 이는 DP 테이블에 “다음 칸을 계산하려면 이전 칸들이 먼저 계산되어야 한다”는 방향성이 있기 때문에 성립한다.

이때 위의 DP 테이블 인덱스(i, j)를 문자열 인덱스와 동일하게 사용하기 위해서는 문자열의 첫 인덱스에는 아무것도 저장하지 않아야 한다. 예를 들어 문자열 배열 s에 "An"을 저장하고자 한다면 s[0]=, s[1]='A', s[2]='n'과 같이 저장된다.

이 알고리즘이 단순 재귀적인 알고리즘과 구분되는 점은 재귀 알고리즘과 같이 D[i][j]를 계산하기 위해서 D[i−1][j], D[i][j−1], D[i−1][j−1]를 또 재귀 호출하는 대신 배열 lookup을 사용하여 단순히 테이블에 저장된 값을 읽기만 하여 훨씬 빠른 속도를 보장[6]하고, parent 포인터를 저장하여 편집 경로를 복원할 수 있다는 것이다. 또한 goal_cell() 같은 일반화된 함수 사용하여 여러 문제로 이를 확장할 수 있다는 장점이 있다.

Dynamic Programming Edit Distance Code

아래는 동적 프로그래밍을 사용한 알고리즘을 C언어로 구현한 것이다: 

int string_compare(char *s, char *t, cell m[MAXLEN+1][MAXLEN+1]) {
    int i, j, k;      /* counters */
    int opt[3];       /* cost of the three options */

    for (i = 0; i <= MAXLEN; i++) {
        row_init(i, m);
        column_init(i, m);
    }

    for (i = 1; i < strlen(s); i++) {
        for (j = 1; j < strlen(t); j++) {

            opt[MATCH]  = m[i-1][j-1].cost + match(s[i], t[j]);
            opt[INSERT] = m[i][j-1].cost   + indel(t[j]);
            opt[DELETE] = m[i-1][j].cost   + indel(s[i]);

            m[i][j].cost   = opt[MATCH];
            m[i][j].parent = MATCH;

            for (k = INSERT; k <= DELETE; k++) {
                if (opt[k] < m[i][j].cost) {
                    m[i][j].cost   = opt[k];
                    m[i][j].parent = k;
                }
            }
        }
    }

    goal_cell(s, t, &i, &j);
    return (m[i][j].cost);
}

Example of Implementation

Figure 1은 "thou shalt"를 "you should"로 편집하기 위한 Edit Distance를 구한 결과 DP 테이블이다. 해당 DP 테이블의 값들은 해당 인덱스가 가리키는 부분문자열을 일치시키기 위해서 요구되는 Edit Distance(편집 횟수)를 의미한다. 예를 들어 m[3, 2]는 "tho"를 "so"로 편집하기 위해서 요구되는 편집 횟수를 의미한다. 이때 각각의 값들은 두 문자열의 마지막 문자를 서로 비교하며 결정되며 사용되는 식은 아래와 같다: 

D[i,j] is minimum of:
• D[i−1,j−1] if S[i]=T[j]: 둘이 같으면 비용 추가 안 됨(match)
• D[i−1,j−1]+1 if S[i]≠T[j]: 둘이 다르면 치환 필요(substitution)
• D[i,j−1]+1 for an insertion into S: T에서 문자를 하나 가져오는 경우(insertion)
• D[i−1,j]+1 for a deletion from S: S에서 문자를 하나 버리는 경우(deletion)
Figure 1. Example of DP Table

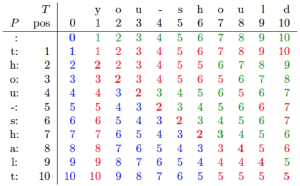
위 연산을 의식하면 DP 테이블에 대해 더욱 깊이 이해할 수 있다. 제시된 DP 테이블에는 색칠이 되어 있는데, 이는 각각의 원소들이 어떠한 연산을 통해 구해졌는지를 의미한다. 먼저, 빨간색은 일치(match)나 치환(substitution)을 의미한다. 즉, 이는 해당 원소의 부모가 되는 원소가 대각선에 일치함을 의미한다. 이때 부모 원소와 비교하여 값이 보존되었다면 일치(M), 값이 증가하였다면 치환(S) 연산을 통해 구해진 것이다. 두번째로, 초록색은 삽입 연산(Insertion)을 의미한다. 즉, 이는 해당 원소의 부모가 되는 원소가 왼쪽에 일치함을 의미한다. 마지막으로, 파란색은 삭제 연산(Deletion)을 의미한다. 즉, 이는 해당 원소의 부모가 되는 원소가 위쪽에 일치함을 의미한다.

이를 통하여 m[10, 10] 부터 연산을 역추적하면 Edit Distance를 5로 만들기 위한 Edit Sequence가 DSMMMMMISMS임을 알 수 있다. 이때 주어진 Edit Sequence에서 M을 제외한 편집 횟수는 5이며, 이는 m[10][10]을 통해 주어진 Edit Distance인 5와 일치한다.

Reconstructing the Path

DP 테이블을 기반으로 연산 경로를 복원하기 위해서는 DP 테이블의 m[|S|][|T|]에서 시작하여 parent를 따라가는 것이다. 즉, goal state인 m[i][j]에서 시작하여 parent 방향으로 (i-1, j), (i, j-1), (i-1, j-1) 중 하나로 이동하며, 이 과정에서 발생한 연산인 M/S/I/D를 기록하면 되는 것이다. 하지만 이는 뒤집혀진 순서이므로, 기록된 것을 reverse하여 출력해야 한다. 혹은 재귀(recursion)를 반대로 실행하면 자동으로 정방향 순서를 구할 수 있다. 아래는 주어진 DP 테이블을 바탕으로 경로를 복원하는 함수를 C언어로 구현한 예시이다: 

void reconstruct_path(char *s, char *t, int i, int j, cell m[MAXLEN+1][MAXLEN+1]) {
    if (m[i][j].parent == -1) {
        return;
    }

    if (m[i][j].parent == MATCH) {
        reconstruct_path(s, t, i-1, j-1, m);
        match_out(s, t, i, j);
        return;
    }

    if (m[i][j].parent == INSERT) {
        reconstruct_path(s, t, i, j-1, m);
        insert_out(t, j);
        return;
    }

    if (m[i][j].parent == DELETE) {
        reconstruct_path(s, t, i-1, j, m);
        delete_out(s, i);
        return;
    }
}

Variant of Edit Distance

Edit Distance 알고리즘을 커스터마이징 하면 다른 많은 문제들에 대해 적용할 수 있다. 이를 하기 위해서는 먼저, row_init() 와 column_init() 함수가 하는 일에 대해 알아야 한다. 이들은 DP 테이블의 0번째 행과 0번째 열을 초기화하는 함수들이다. 이는 각각 아래와 같은 의미이다:

  1. row_init(): 0번째 행 (m[0][j]) = 문자열 S가 비어있을 때 T[1..j]를 만들기 위해 삽입만 j번 해야 함
  2. column_init(): 0번째 열 (m[i][0]) = 문자열 T가 비어있을 때 S[1..i]를 만들기 위해 삭제만 i번 해야 함

즉, 이 함수들이 기본 DP 테이블의 경계 조건(base case)을 설정한다.

하지만 커스터마이징의 핵심은 penalty cost를 조절하는 것이다. penalty cost란 연산 M/S/I/D에 대해 임의로 부여한 비용을 의미한다. 이때 match(c, d)는 문자 c를 d로 바꾸는 비용을 의미한다. 이에 따라 두 문자가 같다면 비용이 0이고, 다르면 일반적으로는 1이다. 또한 indel(c)은 c를 삭제/추가하는데 발생하는 비용을 의미하며, 일반적인 Edit Distance 알고리즘에서는 1비용이 1로 설정된다. 이때 match(c, d)와 indel(c)의 비용을 조절하는 것을 통해서 다양한 커스터마이징을 할 수 있다.

goal_cell() 함수는 traceback이 어디서 끝나는지 결정한다. 기본적인 Edit Distance에서는 목표 셀(goal cell)은 DP 테이블의 오른쪽 아래, 즉 (len(S), len(T))로 자동으로 설정된다. 이는 문자열 S 전체를 문자열 T 전체로 변환해야 하기 떄문이다. 하짐ㄴ substring edit distance처럼 패턴 S가 텍스트 T 어디에나 나타날 수 있을 때는 goal cell이 마지막 행의 최솟값이 될 수 있다. 따라서 이러한 경우에는 goal_cell() 함수를 커스터마이징 해야 한다.

Substring Matching

부분 문자열 매칭(Substring Matching)은 문자열 S(패턴)이 문자열 T(긴 텍스트) 안에서 가장 잘 맞는 위치를 찾는 것을 목표로 한다. 이때 기존의 일반적인 Edit Distance 알고리즘을 그대로 활용하지 않는 이유는 S 전체와 T 전체를 비교하여 S 를 T 로 완전히 바꾸는 비용을 계산하기 때문에 매우 비효율적이기 때문이다. 예를 들어 패턴 S 가 길이 6인데 T 가 길이 2000이면, T 안의 S 위치를 찾기 위해 T 나머지 부분 전체를 delete 해야 한다.

따라서 이러한 문제를 해결하기 위해서는 패턴 매칭 비용이 텍스트 길이에 의존하지 않도록 하는 것이다. 따라서 위에서 구현된 함수를 커스터마이징해야 한다. 먼저 아래는 수정된 row_init() 함수이다: 

void row_init(int i, cell m[][]) {
    m[0][i].cost = 0;
    m[0][i].parent = -1;
}

기존의 초기화 함수는 0행의 편집횟수를 m[0][j] = j으로 설정한 반면에, 위 함수는 0행의 전체 비용을 0으로 만든다. 이를 통해 텍스트 T 의 어느 위치든 “비용 없이” 시작할 수 있게하여 S의 첫 글자와 T의 어떤 위치라도 “매칭 시작점”이 될 수 있도록 한다. 아래는 수정된 goal_cell() 함수이다: 

*i = strlen(s) - 1;
*j = 0;
for (k = 1; k < strlen(t); k++) {
    if (m[*i][k].cost < m[*i][*j].cost)
        *j = k;
}

기존의 편집거리인 goal cell은 (len(S), len(T))이어서 S 전체를 T 전체로 변환하는 비용이었다. 하지만 위 함수는 S 전체가 끝나기만 하면 T 의 어떤 j 위치여도 괜찮아야 하므로 S 의 마지막 행 i = |S| 을 고정하고 그 행 전체에서 최소 비용을 갖는 열 j를 찾는다.

Longest Common Subsequence

LCS(Longest Common Subsequence) 문제는 두 문자열 중에서 가장 긴 공통 부분수열을 찾는 문제이다. 예를 들어 "democrat"과 "republican" 사이의 LCS는 "eca"이다. 이는 e,c,a가 두 문자열 모두에서 인덱스 순서를 유지하는 가장 긴 부분 수열이기 때문이다.

원래의 Edit Distance 알고리즘을 LCS 문제에 그대로 적용하는 것은 부적절하다. 왜냐하면 LCS는 “일치하는 문자”만 중요하고 문자가 다르면 match가 아니라 그냥 버리면(delete)되기 때문이다. 따라서 substitution(치환)을 “금지”하는 방식으로 알고리즘을 커스터마이징해야 한다. 이는 아래와 같은 코드로 구현된다: 

int match(c, d) {
    if (c == d) return 0;
    return MAXLEN;  // 엄청 큰 값 = 사실상 불가능
}

즉, 이를 통해서 DP는 문자가 같으면 match하고, 문자가 다르면 delete/insert로 스킵한다. 이를 통해 가장 많은 match 를 모으는 방향으로 DP가 움직이며, 그 match들의 집합이 바로 LCS가 된다.

LCS 문제를 응용하면 LIS(Longest Increasing Subsequence) 문제도 해결할 수 있다. LIS는 Maximum Monotone Subsequence이라고도 불리며, 이는 원래 수열에서 일부 숫자를 삭제해 증가하는(subsequence) 형태를 유지하면서 가장 긴 수열을 만드는 문제이다. 예를 들어 243517698에서 LIS는 23568이다. 이는 LIS는 LCS 문제와 동일하기 때문이다. 이는 문자열 S가 있을 때, 아래와 같은 과정을 통해서 풀 수 있다:

  1. S를 정렬(sorted) 해서 새로운 수열 T를 만든다.
  2. LCS(S, T)를 구한다.
  3. 그 LCS가 바로 LIS이다.

각주

  1. ↑ 예를 들어, shot → spot의 경우는 ‘g’를 삽입하므로 Insertion 1회에 해당한다.
  2. ↑ 예를 들어, ago → agog의 경우는 ‘h’를 ‘p’로 바꾸므로 Substitution 1회에 해당한다.
  3. ↑ 예를 들어, hour → our의 경우는 ‘h’ 삭제 → Deletion 1회에 해당한다.
  4. ↑ (s[1..i-1], t[1..j-1])에 해당한다.
  5. ↑ 혹은 S에 문자를 추가하거나 삭제하는 방식을 취할 수도 있다.
  6. ↑ 시간 복잡도가 O(|S|×|T|)로 줄어든다.
원본 주소 "https://junhoahn.kr/junyoung/index.php?title=Edit_Distance&oldid=4043"