Shortest Paths

개요

해당 문서에서는 그래프에서의 최단 경로(shortest path)를 찾는 알고리즘을 설명한다.

Applications for Shortest Paths

그래프 상 두 노드 간 최단 경로를 찾는 문제는 실제 여러 분야에서 나타나며, 아래와 같다:

교통 문제(Transportation problems): 두 지점 사이의 가장 저렴하거나 빠른 이동 경로를 찾는 문제
- 대표적인 사례가 네트워크 라우팅이며, 이는 LS 라우팅 알고리즘 문서에서 자세히 확인할 수 있다.
이동 계획(Motion planning): 로봇이나 캐릭터가 장애물을 피해 이동하는 경로를 구하는 문제.
통신 문제(Communications problems): 두 노드 간 신호 전송이 가장 빠른 경로를 찾는 문제

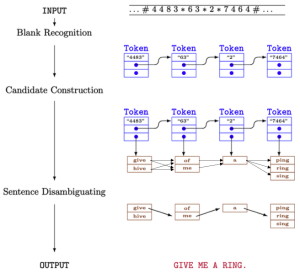
또한, 자연어 처리에 최단 경로 문제를 응용할 수 있다. 숫자키를 이용하여 문자를 입력하고자 할때, 여러 단어 후보가 생긴다. 예를 들어 4483을 입력한다면 가능한 단어는 “give” 또는 “hive”이다. 이때 각 가능한 단어를 정점(vertex) 으로, 단어 간 가능한 연결 관계를 간선(edge) 으로 표현할 수 있다. 따라서 최단 경로 문제를 활용하여 문장 해석을 하는 것은, 가능한 후보 중 의미적으로 가장 자연스러운 조합(=가장 짧은 경로) 를 찾는 과정이다. 이 과정은 figure 1에 잘 나타나 있다. 이때 그래프에는 간선(단어 간 연결)에 “확률 기반 가중치(weight)”를 부여해야 한다. 이는 두 단어가 문장에서 인접할 확률을 기반으로 한다. 이 경우에는 Dynamic Programming 또는 Viterbi 알고리즘을 사용해 DAG(Directed Acyclic Graph) 내에서 최소 가중치 경로를 찾아야 한다.

Kind of Shortest Paths Problem

최단 경로 문제의 가장 기본적인 형태는 가중치 그래프(weighted graph)에 대한 것이다. 그 이유는 가중치 그래프에 대한 최단 경로가 도로 문제 등 다양한 문제에서 활용될 수 있기 때문이다. 하지만 최단 경로 문제는 그래프의 특성에 따라 여러 가지 고려할 점이 존재하며, 해당 문단에서는 이에 대해 설명한다.

Unweighted Graphs

비가중 그래프(Unweighted Graph)는 모든 간선의 비용이 동일한 그래프를 의미한다. 따라서 비가중 그래프에서의 최단 경로는 가장 적은 간선을 지나는 경로이다. 이는 n개의 정점과 m개의 간선이 주어졌을 때, BFS(Breadth-First Search)로 O(n + m) 시간에 해결 가능하다. 하지만 BFS 그래프를 가중 그래프에 적용할 수는 없는데, 이는 여러 개의 작은 간선을 지나는 게 한 개의 큰 간선을 지나는 것보다 더 저렴할 수 있기 때문이다.

Negative Edge Weights

그래프에 대해 음수 가중치 간선(negative edge) 이 존재하면 문제가 복잡해진다. 이는 “음수 가중치 순환(negative cycle)”이 있으면, 무한히 돌면서 비용을 계속 줄일 수 있어 최단 경로가 정의되지 않기 때문이다. 예를 들어, A → B → C → A 로 돌아오는데 합이 -3이라면 계속 순환할수록 더 짧은 경로가 생기므로 의미 없는 결과가 된다. 따라서 일반적으로는 모든 가중치를 양수라고 설정하며, 특히 Dijkstra는 양수 가중치만 다루는 알고리즘이다. 예외적으로 Bellman-Ford 알고리즘 등은 음수 가중치를 처리할 수 있다. 이때 MST(Minimum Spanning Tree)는 음수 가중치와 상관없으므로 이에 대해 혼동하면 안된다.^[1]

Dijkstra’s Algorithm

다익스트라 알고리즘(Dijkstra’s Algorithm)은 간선의 가중치가 양수인 가중치 그래프에서의 최단 경로를 탐색하는 알고리즘이다. 다익스트라 알고리즘의 핵심 원리는 부분 최적성(Optimal Substructure)이다. 부분 최적성이란, 만약 경로 s→…→x→…→t 가 최단 경로라면, 그 일부인 s→…→x 도 역시 최단 경로여야 한다는 뜻이다. 이를 이용하여 Dynamic Programming 방식으로 접근할 수 있다. 이는 이미 구한 가까운 노드들의 최단 경로 정보를 이용해 점점 멀리 있는 노드들의 최단 경로를 확장해 나가는 구조이다.

How Dijkstra’s Algorithm works

다익스트라 알고리즘의 시작 단계(Initialization)에서는 출발점 s에서 각 노드까지의 거리를 초기화한다. 이는 아래와 같다:

d(s, s) = 0 (자기 자신까지의 거리는 0)
나머지 노드는 무한대로 설정한^[2] 후, 정점 s에서 연결된 간선들을 이용해 인접 노드의 거리값을 갱신한다.

다익스트라 알고리즘은 시작 단계 이후, 주어진 거리 배열(distance array)를 업데이트(update)하며 최단 경로를 탐색한다. 이는 정점 s에서 어떤 정점 x에 대한 최단 경로가 확정되면, 그 노드와 연결된 모든 간선을 검사해 s→x→y 가 기존 s→y보다 짧은지 확인하고 갱신하는 방식이다. 즉, 거리 배열(distance array)을 유지하면서 새 노드를 확정할 때마다 그 이웃 노드들의 거리값을 업데이트하는 방식이다. 아래는 다익스트라 알고리즘에 대한 수도 코드이다:

//initialize
known = {s}
for i = 1 to n, dist[i] = <math>\infty</math>
for each edge (s, v), dist[v] = d(s, v) //s와 연결된 정점에 대해 dist 업데이트
last = s //마지막으로 확정된 정점

//update
while (last <math>\neq</math> t) //t는 목표 정점
       select v such that dist(v) = min<sub>unknown</sub>(dist(i))
       for each edge (v, x):
           dist[x] = min(dist[x], dist[v] + w(v, x))
       last = v
       known = known <math>\cup</math> {v}

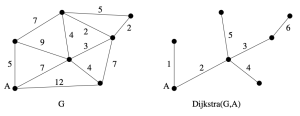
위 수도 코드에서 known 집합은 “최단 경로가 확정된 정점들”을 의미한다. 이때 각 과정에서는 아직 확정되지 않은 노드 중 가장 dist 값이 작은 것을 선택하여 dist값을 확정하며, 선택된 노드의 모든 인접 노드에 대해 거리를 갱신한다. 이 과정을 반복하여 최단 경로를 탐색한다. Figure 2는 다익스트라 알고리즘을 실행한 예시 결과이다.

다익스트라 알고리즘은 Prim 알고리즘과 유사하다. 이는 Prim도 “가장 작은 비용으로 확장하는 구조”를 사용하며, 둘 다 “가장 가까운 정점부터 추가”라는 탐욕적(greedy) 구조를 가지기 때문이다.

다익스트라 알고리즘은 배열 자료구조를 기반으로 하는 경우 Prim 알고리즘과 마찬가지로 O(n²)의 시간 복잡도를 가진다. 이는 각 정점에 대해 아직 포함되지 않은 노드 중 최솟값을 찾기 위해 O(n) 시간이 걸리기 때문이다. 하지만 단순 배열 대신 priority queue자료 구조를 사용하면 속도를 개선할 수 있다.
먼저 Binary Heap(이진 힙)을 사용하는 경우, 각 정점을 현재까지의 거리 distance[v] 기준으로 정렬해두고 “가장 짧은 거리의 정점”을 O(log n) 시간에 꺼낼 수 있다. 이 경우 시간 복잡도는 아래와 같이 계산된다:

정점을 꺼내는 작업은 n번 일어나며, 각각 O(log(n))의 시간복잡도를 가진다. → O(n log(n))
거리 갱신(relaxation)은 각 간선마다 최대 한 번 일어난다. → O(m log(n))
총 시간 복잡도: O((n+m)log(n))

이보다 더욱 효율적인 자료구조는 Fibonacci Heap이다. Fibonacci Heap은 Binary Heap보다 더 효율적인 우선순위 큐이며, 핵심 차이점은 decrease-key 연산이 매우 빠르다는 것이다. decrease-key 연산이란 아래와 같이 다익스트라에서 어떤 간선을 완화(relaxation)할 때:

if (distance[w] > distance[v] + weight(v,w))
    distance[w] = distance[v] + weight(v,w);

이처럼 기존 거리보다 짧은 경로를 발견하면 힙에서 해당 정점의 키(거리값)를 줄여야 하는데, 이 연산을 decrease-key 라고 부른다. 해당 연산은 Binary Heap에서는 O(log(n))의 시간 복잡도가 소요되지만, Fibonacci Heap에서는 평균 O(1)만에 수행 가능하다. 이에 따라 시간 복잡도는 O(nlog(n)+m)이 된다.

Dijkstra’s Implementation

int dijkstra(graph *g, int start) {
    int i;              /* counter */
    edgenode *p;        /* temporary pointer */
    bool intree[MAXV+1];/* is the vertex in the tree yet? */
    int distance[MAXV+1];/* cost of adding to tree */
    int v;              /* current vertex to process */
    int w;              /* candidate next vertex */
    int dist;           /* cheapest cost to enlarge tree */
    int weight = 0;     /* tree weight */

    for (i = 1; i <= g->nvertices; i++) {
        intree[i] = false;
        distance[i] = MAXINT;
        parent[i] = -1;
    }

    distance[start] = 0;
    v = start;

    while (!intree[v]) {
        intree[v] = true;
        if (v != start) {
            printf("edge (%d,%d) in tree \n", parent[v], v);
            weight = weight + dist;
        }

        p = g->edges[v];
        while (p != NULL) {
            w = p->y;
            if (distance[w] > (distance[v] + p->weight)) {   /* CHANGED */
                distance[w] = distance[v] + p->weight;       /* CHANGED */
                parent[w] = v;                               /* CHANGED */
            }
            p = p->next;
        }

        dist = MAXINT;
        for (i = 1; i <= g->nvertices; i++) {
            if ((!intree[i]) && (dist > distance[i])) {
                dist = distance[i];
                v = i;
            }
        }
    }

    return(weight);
}

Floyd’s Algorithm

Floyd 알고리즘은 그래프의 모든 정점 쌍 간 최단 경로(All-Pairs Shortest Path) 를 찾는 알고리즘이다. 하나의 정점 s로부터 다른 모든 정점까지의 최단경로는 Dijkstra 알고리즘으로 구할 수 있다. 하지만 모든 정점 쌍 사이의 최단 경로를 찾기 위해서 Dijkstra를 n번 실행하면 대략 O(n³)의 시간 복잡도가 소요된다. 따라서 모든 정점 쌍 사이의 최단 경로를 더욱 효율적으로 찾고자 하는 것이 Floyd 알고리즘의 시작점이다.

Dynamic Programming

Floyd 알고리즘은 동적 프로그래밍을 기반으로 한다. 동적 프로그래밍은 아래와 같은 단계를 통해 문제를 해결한다:

최적해의 구조를 파악한다.(Optimal Substructure)
그 값을 재귀적으로 정의한다.(Recurrence)
Bottom-up 방식으로 계산한다.
계산된 값으로부터 최적해를 복원한다.

따라서, Floyd 알고리즘을 수행하기 위해서는 아래와 같이 인접 행렬(Adjacency Matrix)로부터 초기 거리 행렬 D를 구성해야 한다:

 $D [i, j] = {\begin{cases} 0 & i f i = j \\ w (i, j) & i f e d g e (i, j) \in E \\ \infty, & o t h e r w i s e \end{cases}$

위의 식은 간선 (i,i)의 거리 D[i,i]는 0, 간선 (i, j)가 존재하면 거리 D[i,j]는 w(i,j), 간선 (i, j)가 존재하지 않으면 그 거리 D[i,j]는 무한대라는 것을 의미한다. 이때 동적 프로그래밍의 상태 정의는 아래와 같다:

$d [i, j]^{k}$ : 1~k번 정점만을 중간 노드로 사용할 수 있을 때, i→j의 최단거리
즉, k가 커질수록 고려할 수 있는 중간노드의 집합이 확장됨.
경로는 vertex k를 “지나거나(through k)” 또는 “지나지 않거나” 두 경우 뿐이다.

이를 기반으로 아래와 같이 점화식(Recurrence Relation)을 세울 수 있다:

 $d [i, j]^{k} = m i n (d [i, j]^{k - 1}, d [i, k]^{k - 1} + d [k, j]^{k - 1})$

즉, 위 점화식은 “i에서 j로 갈 때 vertex k를 거치는 것이 더 짧은가?”를 확인해서 갱신하는 것이다. k를 거치지 않은 최단거리 vs k를 거치는 경로의 거리 중 더 짧은 걸 선택하고, 이렇게 k=1→n 순서로 모든 정점을 중간노드로 고려하면, 최종적으로 모든 쌍의 최단경로를 완성할 수 있다.

Implementation of Floyd's Algorithm

아래는 Floyd 알고리즘의 수도코드이다.

d⁰ = w
for k = 1 to n:
    for i = 1 to n:
        for j = 1 to n:
            d[i,j] = min(d[i,j], d[i,k] + d[k,j])

위에서 시간복잡도는 Dijkstra n회와 복잡도는 같은 O(n³)이지만, Floyd 알고리즘은 구현이 단순하고 상수 계수가 작아 더 빠르게 작동한다. 아래는 이를 C언어로 구현한 코드이다:

typedef struct {
    int weight[MAXV+1][MAXV+1];
    int nvertices;
} adjacency_matrix;

void floyd(adjacency_matrix *g) {
    int i, j, k, through_k;
    for (k = 1; k <= g->nvertices; k++) {
        for (i = 1; i <= g->nvertices; i++) {
            for (j = 1; j <= g->nvertices; j++) {
                through_k = g->weight[i][k] + g->weight[k][j];
                if (through_k < g->weight[i][j]) {
                    g->weight[i][j] = through_k;
                }
            }
        }
    }
}

Transitive Closure

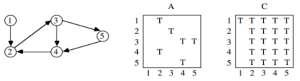
Floyd 알고리즘을 활용하여 가중치가 아니라 연결 여부(True/False) 만 고려하여 Transitive Closure에 활용할 수 있다. 이를 위해 아래와 같은 식을 만들 수 있다:

 $C [i, j] = 1 i f t h e r e e x i s t s a p a t h i \to j$

위 식을 이용하여 Floyd 알고리즘의 논리를 그대로 Boolean 연산으로 적용할 수 있다:

 $C [i, j] = C [i, j] \lor (C [i, k] \land C [k, j])$

Figure 3는 이를 쉽게 설명한 예시이다.

각주

↑ MST는 자체 정의에 의해서 사이클을 배제한 트리를 의미하기 때문이다.
↑ 다른 정점에 대한 거리를 모르기 때문이다.

[1] MST는 자체 정의에 의해서 사이클을 배제한 트리를 의미하기 때문이다.

[2] 다른 정점에 대한 거리를 모르기 때문이다.

[1]

[2]

익명 사용자

검색

Shortest Paths

이름공간

더 보기

문서 행위

목차

개요

Applications for Shortest Paths

Kind of Shortest Paths Problem

Unweighted Graphs

Negative Edge Weights

Dijkstra’s Algorithm

How Dijkstra’s Algorithm works

Dijkstra’s Implementation

Floyd’s Algorithm

Dynamic Programming

Implementation of Floyd's Algorithm

Transitive Closure

각주

둘러보기

둘러보기

위키 도구

위키 도구

익명 사용자

검색

Shortest Paths

개요

Applications for Shortest Paths

Kind of Shortest Paths Problem

Unweighted Graphs

Negative Edge Weights

Dijkstra’s Algorithm

How Dijkstra’s Algorithm works

Dijkstra’s Implementation

Floyd’s Algorithm

Dynamic Programming

Implementation of Floyd's Algorithm

Transitive Closure

각주

둘러보기

위키 도구

문서 도구

분류 목록