Pushdown Automaton

youngwiki
Pinkgo (토론 | 기여)님의 2025년 10월 30일 (목) 04:30 판 (→CFG from PDA Example)

상위 문서: Context-Free Languages

개요

정규 언어를 다루기 위해서는 FA(Finite Automaton)으로 충분하지만, 그보다 더 일반적인 언어인 CFG(Context-Free Languages)를 다루기 위해서는 PDA(Pushdown Automaton)[1]>가 사용된다. PDA는 FA의 한계를 보완하기 위해서 추가적인 기억 장치인 stack을 활용하며, 이를 통해서 추가적인 '기억'을 구현할 수 있다. 예를 들어 아래와 같은 언어를 고려해보자: 

L={wwR|w∈Σ*}

이는 아래와 같은 작동 과정을 거친다:

  1. 입력의 앞부분 w를 스택에 차례로 push 한다.
  2. w가 끝났다고 nondeterministically guess(추측)한다.
  3. 이후 입력의 나머지 부분을 읽으며, 스택에서 pop한 심볼과 비교한다.
  4. 모두 일치하고 스택이 비면 해당 문자열은 PDA에 의해서 accept된다.

이때, 모든 NFA는 PDA의 특수한 경우로 볼 수 있다. 왜냐하면 PDA는 스택을 가진 오토마타지만, 스택을 전혀 사용하지 않게 정의하면 그건 곧 NFA와 동일한 동작을 하기 때문이다. 이를 통해서 아래와 같은 명제가 성립한다: 

Context-Free Languages ⊇ Regular Languages

Formal Definition of nondeterministic PDA

PDA는 아래와 같은 5-튜플(Q,Γ,Σ,δ,q0,F)로 정의할 수 있다:

  • Q: 유한 상태 집합
  • Σ: 입력 알파벳
  • Γ: 스택 알파벳
  • δ: Q×Σ→Q: 전이 함수(transition function), 현재 상태와 입력 기호를 다음 상태로 매핑
    • δ:Q×Σϵ×Γϵ→P(Q×Γϵ)
    • 현재 상태, 입력 알파벳, 스택의 top 알파벳에 따라 여러 (r,b)∈δ(q,w,a) 쌍을 반환한다.
  • q0∈Q: 시작 상태(start state)
  • F⊆Q: 수용 상태 집합(a set of accept states)

이때 전이함수는 nondeterministic PDA 위에서 정의되므로 주어진 전이 함수 δ(q,w,a)는 여러 (r,b) 쌍을 가질 수 있다. 이때 (r,b)∈δ(q,w,a)는 현재 상태가 q이고, 입력 알파벳이 w, 스택의 top 알파벳이 a일 때, 상태 r로 전이하며 스택에서 a를 pop하고 b를 push한다는 것을 의미한다. 만약 (r,b)∈δ(q,w,a)에서 a=ϵ이면 스택을 pop하지 않는 것이고, b=ϵ이라면 스택에 push하지 않는 것이다. 이때 PDA의 스택이 비었는지를 직접 검사하는 것은 불가능하지만, 특수기호 $ 를 스택 바닥에 push하여 비어있음을 간접적으로 확인할 수 있다.

Computation of a PDA

PDA P가 입력 w=w1w2⋯wm을 수용(accept)한다는 것은 일련의 상태열 r0,r1,⋯rm과 스택 문자열열 s0,s1,⋯,sm이 존재해야 한다. 이를 위한 조건은 아래와 같다:

  1. r0=q0,s0=ϵ: PDA는 처음에 초기 상태 q0에서 시작하고 스택이 비어있다.
  2. For i=0,1,⋯,m−1, (∃ai,bi∈Γϵ)∧(t∈Γ*) such that (si=ait,si+1=bit)∧((ri+1,bi)∈δ(ri,wi+1,ai))
    • 아래는 이를 쉽게 풀이한 것이다:
    1. 현재 스택의 내용이 si=ait 형토로 되어 있다면(즉, top에 ai가 있다면)
    2. 입력 심볼 wi+1를 읽고,
    3. PDA의 전이함수 δ에 따라 ai를 pop하고 bi를 push하여 스택의 나머지 부분 t를 보존한다.
    4. 그 결과 PDA는 새로운 상태 ri+1에 도달한다.
    • 즉, DA가 스택의 맨 위를 조작하며 상태를 바꾸는 한 단계의 이동 규칙을 수학적으로 적은 것이다.
  3. rm∈F: 마지막으로 PDA가 모든 입력을 처리한 후 accept 상태 집합 F에 속하는 상태에 도달해있다.

Computation Example

Figure 1. PDA Example 1

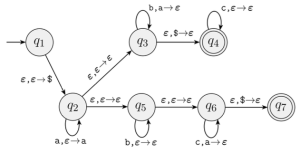
Figure 1은 아래 언어를 나타내는 언어의 구현을 나타낸 것이다: 

L={aibjck|i,j,k≥0∧(i=j∨i=k)}

즉, a,b,c의 개수 관계가 i=j 또는 i=k인 문자열을 인식한다. 아래는 Figure 1에 나타난 PDA에 대한 설명이다:

  1. q1→q2: 시작 시 스택에 기호 $ 삽입 (스택바닥표시).
  2. q2: a를 읽을 때마다 a를 push.
  3. q2→q3: ϵ 전이를 통해 “a와 b 개수를 비교하는 경로”로 진입
  4. q3: b를 읽을 때마다 a를 popg하여 i=j인 경우를 처리.
  5. q4: i=k이므로 수용 상태에 계속 머무른다.
  6. q5∼q7: 다른 경로 (nondeterminism)로 두 경우 모두 처리 가능하도록 설계.

PDA and CFG

PDA’s from CFG’s

모든 CFG는 어떤 PDA에 의해 인식되며, 이는 CFG→PDA 변환이 가능하다는 뜻이다. 이때 CFG를 PDA로 변환하는 것은 아래와 같이 스택을 이용하여 실현된다:

  1. 스택은 아직 남은 입력 문자열을 도출하기 위해 필요한 문장형식(sentential form)을 유지한다.
    • CFG에서 문장을 생성할 때에는 "시작 비단말기 S"에서 여러 변환 규칙을 걸치면서 생성된다.
    • PDA에서는 스택에 그 현재 문장형식(예: S→aSb→aabb) 의 “아직 처리되지 않은 부분”을 저장한다.[2]
  2. 스택의 top에 단말기가 있을 때, 그것이 현재 입력 문자열의 첫 글자와 비교한다.
    • 두 문자가 같다면 스택에서 pop하고 입력에서도 consume한다.
    • 같지 않다면 PDA의 그 “계산 경로(computation path)”는 실패한다.
  3. 만약 스택의 top이 비단말기라면, CFG의 생성 규칙 중 하나를 비결정적(nondeterministically) 선택한다.
    • 만약 선택된 생성 규칙이 A→aBb라면, 스택의 top인 A를 pop하고, b,B,a를 역순으로 push한다.
  4. 스택의 내용이 다 처리되어 비면[3] PDA는 accept state 로 이동한다.[4]

PDA's states

CFG에서 만든 PDA는 아래와 같은 세 가지 핵심적인 상태를 가진다:

  1. qstart: 시작 상태
    • 스택에 $S를 push한다.[5]
    • 다음 상태는 qloop이다.
  2. qloop: 반복 상태
    • 스택의 top이 단말기면 입력과 비교하여 “match” 후 pop한다.
    • 스택의 top이 비단말기면 CFG의 생성 규칙 중 하나를 비결정적으로 선택하여 스택을 확장한다.
    • 스택의 top이 $이면 qaccept로 이동
  3. qaccept: Accept 상태
    • 스택이 완전히 비고 입력이 끝난 상태이다.

이때 만약 여러 symbol을 한꺼번에 push해야 할 때는, “extra states”를 임시로 만들어 연속 push를 구현한다.

PDA from CFG Example

Figure 2. PDA Example 2

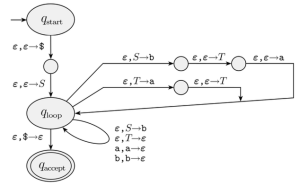
아래와 같은 CFG가 주어졌다고 가정해보자: 

S→aTb|b
T→Ta|ϵ

이를 구현하기 위해서는 qstart,qloop,qaccept를 구현해야 하며, 스택을 CFG 규칙에 맞추어 조작해야 한다. 이는 figure 2를 관찰하면 어떻게 구현이 되었는지 잘 이해할 수 있다.

CFG’s from PDA’s

모든 PDA는 어떤 CFG를 생성하는데, 이는 PDA→CFG 변환이 가능하다는 뜻이다. 이를 CFG의 비단말기는 Apq 형태로 만든다.[6] 이때 아래의 식이 성립한다: 

Apq⇒*w⇔PDA가 입력되는 w를 읽으면서 상태 p에서 q로 이동하고, 스택이 완전히 비워짐

즉, CFG의 규칙은 PDA의 이동경로를 기반으로 구성된다. 또한 아래는 CFG를 만들기 위한 PDA 단순화 전제이다:

  1. PDA P는 정확히 하나의 Accept 상태 qaccept 만을 가진다.
  2. Accept 상태에 도달하기 위해서는 스택이 완전히 비워져야 한다.
  3. 각 전이함수는 push 하나 또는 pop 하나만 수행한다.

Definition of G

위의 내용을 사용하여 CFG를 구체적으로 아래와 같이 정의한다:

  1. 변수 집합: V={Apq|p,q∈Q}
    • 각 변수는 PDA의 상태 p에서 시작해, 상태 q에서 끝나는 모든 문자열들을 생성하는 비단말기를 의미한다.[7]
  2. 시작 변수: S=Aq0,qaccept[8]
  3. 생성 규칙: “u를 스택에 넣고 다시 꺼내는 과정 사이에 있는 계산 전체”를 문법 규칙 하나로 표현한다:
    1. (r,u)∈delta(p,a,ϵ)∧(q,ϵ)∈δ(s,b,u)이면 Apq→aArsb이다.[9]
    2. Apr→ApqAqr
    3. App→ϵ[10]

이러한 규칙을 통해 CFG가 PDA의 “스택 조작 기반 계산 경로”를 그대로 재현할 수 있다.

CFG from PDA Example

Figure 3. CFG from PDA Example

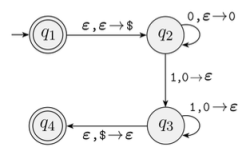
Figure 3에서 CFG는 아래와 같이 유도된다: 

A14→A23 ($를 push한 후, $를 pop)
A23→0A231 (0을 push한 후, 0을 pop)
A23→0A221 (0을 push한 후, 0을 pop)
A22→ϵ

위에서 A14는 PDA의 시작 상태 q1에서 accept 상태 q4까지 가는 모든 입력 문자열을 생성하는 비단말기이다. 따라서 해당 비단말기는 주어진 PDA가 인식하는 언어 전체를 생성해야 하므로 S=A14가 PDA로부터 정의되는 문법의 시작 기호 역할을 한다.

A14→A23과 같은 규칙은 아래의 두 전이: 

(q1,ϵ,ϵ)→(q2,$)
(q3,ϵ,$)→(q4,ϵ)

을 $에 대한 push와 pop의 짝으로 연결한 것이다. 첫 단계에서는 스택에 $를 push하며, 마지막 단계에서는 $를 스택에서 pop한다. 이에 따라 A23는 두 단계 사이의 계산, 즉 PDA의 q2에서 q3까지의 계산을 의미하는 비단말기이다. 즉, A14→A23 규칙은 q1에서 $를 push하는 것으로 시작해 q4에서 $를 pop하며 끝나는 전체 계산은 q2에서 q3 사이에서의 계산과 같다는 것을 의미한다.

A23→0A231과 같은 규칙은 아래의 두 전이: 

(q2,0,ϵ)→(q2,0)
(q3,1,0)→(q3,ϵ)

을 0에 대한 push와 pop의 짝으로 연결한 것이다. 또한 A23→0A221과 같은 규칙은 아래의 두 전이: 

(q2,0,ϵ)→(q2,0)
(q2,1,0)→(q3,ϵ)

을 0에 대한 push와 pop의 짝으로 연결한 것이다. 이때 다른 두 비단말기에 비해 이질적인 A22은 그 정의에 따르면 PDA가 q2에서 시작해서 다시 q2로 돌아오는 과정에서 스택의 상태가 처음과 같게 유지되는 모든 문자열들의 집합을 표현하는 비단말기이다. 이에 따라 스택이 유지되기 위해서는 push와 pop의 수가 같아야 하므로, A33에서 유도될 수 있는 문자열은 ϵ 뿐이다.

각주

  1. ↑ 해당 문서에서는 특별한 언급이 없는 이상 nondeterministic PDA를 기본으로 하여 서술한다.
  2. ↑ 즉, 스택은 “현재 어디까지 유도했는지”를 나타낸다.
  3. ↑ 스택의 top이 $기호인 경우이다.
  4. ↑ 이는 모든 입력이 정확히 문법으로부터 생성될 수 있다는 뜻이다.
  5. ↑ S는 시작 비단말이고, $는 스택의 바닥을 표시한다.
  6. ↑ p, q는 PDA의 상태 집합의 원소이다.
  7. ↑ 쉽게 말하면, “상태 p에서 시작해서 q로 갈 수 있는 입력 문자열”을 대표하는 문법 기호이다.
  8. ↑ PDA의 시작 상태 q0에서 accept 상태까지 가는 문자열을 생성해야 하므로, 문법의 시작기호는 이렇게 설정됩니다.
  9. ↑ p에서 q로 가는 계산은 a를 읽고 u를 푸시한 뒤, 중간에 r에서 s로 이동하면서 u를 팝하며 b를 읽는다는 것을 나타낸다.
  10. ↑ 같은 상태에서 아무 동작 없이 스택이 빈 경우이다.
원본 주소 "https://junhoahn.kr/junyoung/index.php?title=Pushdown_Automaton&oldid=3907"