Regular Expressions

youngwiki
Pinkgo (토론 | 기여)님의 2025년 9월 29일 (월) 15:44 판 (→Converting GNFA to RE)

상위 문서: Regular Languages

개요

정규 표현식(regular expression)은 문자열에서 특정한 패턴을 찾거나 치환·검증하기 위해 사용하는 표현식이다.

Formal Definition of Regular Expressions

정규 표현식 집합 ℛℰ는 알파벳 집합 Σ에 대해 아래의 닫힘 조건(closure conditions)을 만족하는 최소 집합을 의미한다:

  1. a∈ℛℰ,∀a∈Σ
  2. 빈 문자열 ϵ에 대해, ϵ∈ℛℰ
  3. 어떤 문자열도 포함하지 않는 공집합 ∅에 대해, ∅∈ℛℰ
  4. Union: If R1∈ℛℰ,R2∈ℛℰ, then (R1∪R2)∈ℛℰ
  5. Concatenation: If R1∈ℛℰ,R2∈ℛℰ, then (R1∘R2)∈ℛℰ
  6. Kleene Star: If R1∈ℛℰ, then (R1*)∈ℛℰ

이때 정규 표현식은 단순히 문자열(strings)이며, {∅,ϵ,(,),∪,∘,*}∪Σ라는 알파벳 집합 위에서 정의된다. 따라서, a∪b라는 정규표현식이 문자열로 해석되어 단순히 알파벳 a,∪,b의 조합인지, 혹은 정규표현식 a,b의 합집합으로 해석되는지는 맥락에 따라 달라진다.

Structural Induction for RE

어떤 성질 P(R)이 모든 정규 표현식 R에 대해 성립함을 보이고 싶다면 먼저, 아래와 같은 기본 케이스를 규정해야 한다: 

1. P(a),∀a∈Σ 
2. P(ϵ),P(∅)

이를 바탕으로 두 ℛℰR1,R2에 대해 P(R1),P(R2)가 성립한다고 가정하면, 아래도 성립함을 보인다: 

1. P(R1∪R2)
2. P(R1∘R2)
3. P((R1*))

이 과정을 거치면 P(R)은 모든 정규 표현식 R에 대해 참이라는 결론을 얻을 수 있다.

The Language Denoted by a Regular Expression

아래는 정규 표현식 R이 나타내는 언어 L(R)을 귀납적으로 정의한 것이다:

  • L(a)={a} → 단일 문자열 { "a" }.
  • L(∅)=∅ → 아무 문자열도 없음.
  • L(ϵ)=ϵ → 오직 빈 문자열 하나만.
  • L(R1∪R2)=L(R1)∪L(R2)
  • L(R1∘R2)=L(R1)∘L(R2) → R1의 문자열과 R2의 문자열을 이어붙여 생성.
  • L(R1*)=(L(R1))* → R1이 만드는 문자열들의 0번 이상의 반복.

이때 아래와 같은 중요한 정리(Lemma)가 존재한다. 

 For all regular expressions R the language L(R) is a regular language.

이를 증명하기 위해서는 구조적 귀납법(Structural Induction)을 사용하며, 이를 위해 아래의 명제들을 증명해야 한다:

Figure 1. NFA for L(a)
Figure 2. NFA for L(ϵ)
Figure 3. NFA for L(∅)
  1. ∀a∈Σ,L(a) is a regular language.
  2. L(ϵ) is a regular language.
  3. L(∅) is a regular language.
  4. L(R1∪R2)=L(R1)∪L(R2) is a regular language.
  5. L(R1∘R2)=L(R1)∘L(R2) is a regular language.
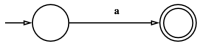
  6. L(R1*)=(L(R1))* is a regular language.

먼저, 명제 1, 2, 3들은 figure 1, 2, 3에 제시된 NFA를 통해 나타내어진다. 또한, 정규 언어들은 각 연산에 대해 닫혀(close)되어 있으므로, 명제 3, 4, 5번또한 성립한다고 할 수 있다.

Simplifying Operators

연산자 우선순위를 설정하여 괄호를 생략할 수 있는데, 그 순서는 ∪<∘<*(Kleene Star)와 같다. 또한 ∘ 기호를 생략하여 보통 문자열 처럼 붙여 쓸 수 있다. 따라서, 01*과 같은 정규 표현식은 0∘(1*)과 같다. 또한 아래는 복잡한 정규 표현식을 단순화한 예시이다. 

R≡(0∪(1∪(0(((0∪1)*)0))∪(1(((0∪1)*)1))))
R≡0∪1∪0(0∪1)*0∪1(0∪1)*1

위의 예시는 사람이 읽기에 훨씬 편하도록 R을 만든 것이다. 이는 연산자 우선순위 규칙과 괄호 생략 규칙을 도입한 이유이다.

Constructing a RE from a NFA

모든 정규 언어는 정규표현식으로 표현될 수 있다. 즉, NFA가 주어지면 반드시 동치인 정규표현식이 존재한다. 이는 아래와 같은 정리(Lemma)를 통해 나타낼 수 있다: 

If L is a regular language, then L = L(R) for some regular expression R.

이를 증명하는 방법은 상태 제거 절차(state elimination procedure)이며, 이는 NFA의 상태들을 하나씩 제거하면서, 그 상태를 통과하는 경로들을 정규표현식으로 바꿔가며 단순화하는 것이다. 이때 일반적인 NFA는 각각의 전이(transit)에 해당하는 화살표가 단일 문자(혹은 ϵ)으로 라벨링되어 있다. 하지만 상태를 제거하다 보면, 두 상태를 연결하는 경로가 단일 문자가 아니라 정규표현식 전체로 표현되는 경우가 생기며, 이를 더욱 쉽게 나타낼 수 있도록 GNFA(Generalized NFA)라는 개념을 도입할 수 있다. 즉, GNFA는 “전이가 단일 문자 대신 정규표현식으로 라벨링된 NFA”를 의미한다. 주어진 NFA를 GNFA로 치환하는 절차를 포함한 GNFA에 대한 자세한 설명은 GNFA 문서를 참조하면 된다.

Converting GNFA to RE

GNFA에서 RE를 얻는 절차는 기저 조건과, 재귀적 단계로 나뉜다. 먼저 기저 조건은 아래와 같다:

  • 만약 상태가 2개(시작/종료)뿐이면, 답은 δ(qstart,qaccept)이다.

이는 시작 상태에서 종료 상태로 전이하는 라벨이 곧 정규표현식이라는 것을 의미한다. 재귀적 단계는 아래와 같다:

  1. 상태가 2개 초과라면, 제거할 상태 qrip을 하나 선택한다. 이때 qstart,qend는 제외한다.
  2. qrip를 제외한 새로운 상태 집합 Q′=Q−{qrip}을 정의한다.
  3. 이에 따라 전이 δ를 δ′(qi,qj)=R1(R2)*R3∪R4와 같이 재정의한다. 이때 R1,R2,R3,R4는 아래와 같다:
    1. R1=δ(qi,qrip)
    2. R2=δ(qrip,qrip) → 자신으로 돌아오는 루프
    3. R3=δ(qrip,qj)
    4. R4=δ(qi,qj)

qi에서 qj로 가는 경우는 qrip를 거치는 경우와 아닌 경우 두 가지로 나뉜다. 먼저, R4=δ(qi,qj)는 qi에서 qj로 qrip을 거치지 않고 전이가 이뤄지는 라벨을 의미한다.
qrip을 거쳐서 가는 경우는 figure 4와 같이 표현된다. 따라서 이와 같은 경우에서 읽어들이는 문자열은 R1(R2)*R3이다. 따라서 두 경로를 합친 전이 라벨은 δ′(qi,qj)=R1(R2)*R3∪R4이다.

각주

원본 주소 "https://junhoahn.kr/junyoung/index.php?title=Regular_Expressions&oldid=3616"