Hash Table

상위 문서: Data Structures

개요

해시 테이블(Hash Table)은 사전(Dictionary)을 구현하는 데에 매우 실용적인 자료 구조이다. 해시 테이블의 근본적인 아이디어는 배열에서 인덱스만 주어지면 이를 바탕으로 원하는 원소에 즉시 접근할 수 있다는 것이다. 이때 키(key)는 보통 정수(integer)가 아니므로, 임의의 키를 정수 인덱스로 바꾸는 해시 함수(hash function)를 구현하고 응용하는 것이 해시 테이블의 골자이다.

Collisions

Figure 1. Chaining Hash Table

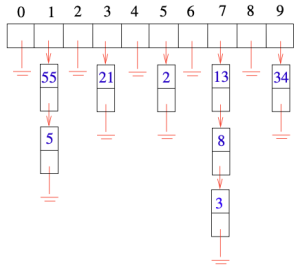
충돌(Collision)이란 서로 다른 두 키가 동일한 해시 값에 매핑되는 현상이다. 충돌이 발생할 경우에는 해당 버킷 안에 여러 키가 모이게 된다. 이때 키들이 해시 함수에 의해 균등(uniformly)하게 버킷들에 분포된다면, 각 버킷에는 몇 안되는 원소들만 들어간다. 따라서 이 경우에는 각 버킷 내부의 작은 리스트만 탐색하면 되므로 여전히 효율적이다. Figure 1은 해시 테이블의 크기가 10인 자료구조에 키 55, 21, 2, 13, 34, 5, 8, 3 등이 해시 값에 따라 여러 버킷에 들어가 있는 것을 보여준다.

Collision Resolution by Chaining

Chaining은 충돌이 발생하였을 때 이를 해결하는 방법중 하나로, 각 버킷마다 연결 리스트(linked list)를 두어 충돌이 발생할 때마다 새 원소를 해당 버킷의 리스트에 추가하는 방식이다. 이는 구현이 단순하고 직관적이라는 장점이 존재하지만, 각 리스트가 포인터를 필요로 하므로 메모리 낭비가 발생한다는 단점이 있다. Figure 1은 Chaining의 한 예시로, 버킷에 해당하는 키 값들이 포인터를 통해 연결되어 있다.

시간 복잡도는 삽입/삭제/탐색 연산이 모두 리스트에서 처리되므로 리스트 길이에 비례한다. 이때 리스트의 길이는 평균적으로 $n/m$이므로 따라서 시간복잡도는 $O(n/m)$이다. 이때 $n/m$은 적재율(load factor)라고 불린다.

Open Addressing

Figure 2. Sequential Open Address

Open addressing은 체이닝 대신 포인터를 쓰지 않고, 테이블 내부에서 다른 빈 공간을 찾아 저장하는 방식이다. 해당 방식은 원래의 해시 값이 가리키는 칸이 비어 있으면 삽입하고, 이미 차 있으면 다음 위치에 삽입하는 것을 시도하는 방식이다. 이때 충돌할 경우 다음 위치를 정하는 규칙은 아래와 같다:

• Sequentially: h,h+1,h+2,...
• Quadratically: h, h+1², h+2², h+3², ...
• Linearly: h, h+k, h+2k, h+3k, ...

Figure 2는 linear probing 방식의 한 예시를 보여준다. 해당 방식은 별도의 포인터 저장이 불필요하다는 장점이 있지만, 원소들이 뭉쳐서 연속 구간을 차지하면(Primary Clustering) 탐색 성능이 저하된다는 단점이 있다. 또한 해당 방식은 원소를 삭제할 때 어려움을 겪는데, 이는 원소를 삭제할 때 단순히 해당 칸을 비워버리면 문제가 생기기 때문이다. 왜냐하면 삭제 이후 탐색 시 “그 원소가 충돌 때문에 다른 칸에 있는지” 구분이 불가능해져서, 일부 원소가 검색 불가능해지기 때문이다. 따라서 보통은 “삭제된 자리”를 특별한 마커(예: DELETED flag)로 표시해 해결한다.

${\displaystyle }$ ${\displaystyle }$