The Big Oh Notation

개요

주어진 어떤 알고리즘에 대한 시간 복잡도는 가능한 문제 인스턴스 크기에 대한 함수들이며, 이들을 정밀하게 다루는 것은 매우 어렵다. 따라서 이들을 단순화하여 분석하는 것이 매우 좋은 방식 중 하나이다. 예를 들어, $T(n)=12754n^2+4353n+834lo{g}_2^n+13546$와 같은 시간 복잡도 함수는 정밀하게 분석하기란 매우 어렵지만, 시간 복잡도가 n에 대해 2차적으로 증가한다는 관찰이 틀렸다고 볼 수는 없다.

해당 문서에서는 이러한 특성을 이용한 “빅 오(Big Oh)” 표기에 대해 알아본다.

내용

Figure 1. Big Oh, Omega, Theta

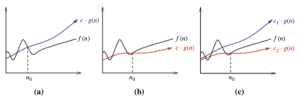
“빅 오(Big Oh)” 표기는 시간 복잡도 함수를 상한/하한으로 나타내어 이를 단순화 하는 방식이다. 함수 $f(n)=2n$과 $g(n)=n$은 빅 오 분석에서 동일하다. 빅 오 표기에는 아래와 같은 세 가지 정의가 존재한다.

• $f(n)=O(g(n))$는 $c\cdot g(n)$가 $f(n)$에 대한 상한임을 의미한다.
  • 따라서 어떤 상수 c가 존재하여 충분히 큰 모든 n에 대하여 $f(n)\le c\cdot g(n)$가 성립한다.
• $f(n)=\mathrm{\Omega }(g(n))$는 $c\cdot g(n)$가 $f(n)$에 대한 하한임을 의미한다.
  • 따라서 어떤 상수 c가 존재하여 충분히 큰 모든 n에 대하여 $f(n)\ge c\cdot g(n)$가 성립한다.
• $f(n)=O(g(n))$는 $c_1\cdot g(n)$가 $f(n)$에 대한 상한이고 $c_2\cdot g(n)$가 $f(n)$에 대한 하한임을 의미한다.
  • 따라서 어떤 상수 c₁, c₂가 존재하여 충분히 큰 모든 n에 대하여 $c_2\cdot g(n)\le f(n)\le c_1\cdot g(n)$가 성립한다.

이러한 정의들은 figure 1에 잘 제시되어 있다. 이들 정의 각각은 어떤 상수 n₀가 존재하여 그 이후에는 조건이 만족된다는 것을 보여준다.

Working with the Big Oh

일반적인 대수 계산을 빅 오 표기에 적용하는 것은 중요하면서도 조금 모호하다. 이는 대부분의 대수 계산에 대한 상식이 유지되면서도 꼭 모두 적용된다고는 말할 수 없기 때문이다.

Big Oh Addition/Subtraction

어떠한 차수가 같은 함수 $f(n),g(n)$에 대해 $f(n)=O(n^2),g(n)=O(n^2)$를 가정해 보자. 이때 함수 $g^{\prime }(n)=f(n)+g(n)$에 대한 빅 오 표기는 아래와 같이 계산할 수 있다.

$f(n)\le c_1\cdot n^2,g(n)\le c_2\cdot n^2$이라 하면
$g^{\prime }(n)=f(n)+g(n)\le (c_1+c_2)n^2,\therefore g^{\prime }(n)=O(n^2)$

즉, 같은 차수의 함수끼리 더해도 결국 그 차수는 변하지 않는다. 하지만 빅 오 표기에서의 뺄셈은 최대 차수의 계수에 따라 그 결과가 달라지기 때문에, 모호하게 작동한다. 예를 들어 함수 $g^{″}(n)=f(n)-|g(n)|$에 대해:

$f(n)=n^2,g(n)=n^2$이라면 , $f(n)-g(n)=0$
$f(n)=2\cdot n^2,g(n)=n^2$이라면, $f(n)-g(n)=n^2$

따라서 어떤 차수가 같은 함수 $f(n),g(n)$에 대해 뺼셈을 진행한다면, 일반적으로 $O(n^2)$라고 말할 수 있을 뿐이며, 해당 차수가 보존되는 지에 대해서는 말할 수 없다.

Multiplying Functions

곱셈은 반복된 덧셈과 같이 취급할 수 있다. 따라서, $c>0$를 만족하는 상수 c에 대해 아래와 같이 계산된다.

$O(c\cdot g(n))\to O(g(n))$
$\mathrm{\Omega }(c\cdot g(n))\to \mathrm{\Omega }(g(n))$
$\mathrm{\Theta }(c\cdot g(n))\to \mathrm{\Theta }(g(n))$

하지만 증가함수인 두 함수를 서로 곱하는 경우에는, 두 함수가 모두 결과에 준다. 이는 아래와 같이 나타낼 수 있다.

$O(f(n))\cdot O(g(n))\to O(f(n)\cdot g(n))$
$\mathrm{\Omega }(f(n))\cdot \mathrm{\Omega }(g(n))\to \mathrm{\Omega }(f(n)\cdot g(n))$
$\mathrm{\Theta }(f(n))\cdot \mathrm{\Theta }(g(n))\to \mathrm{\Theta }(f(n)\cdot g(n))$

Reasoning about Efficiency

알고리즘의 실행 시간에 대한 추론은 보통 쉽다. 이에 대한 예시는 Sorting Problem에 대한 문서를 참조하면 된다.