Relational algebra: 두 판 사이의 차이
편집 요약 없음 |
|||
| 56번째 줄: | 56번째 줄: | ||
===union: <math>\smile</math> === | ===union: <math>\smile</math> === | ||
union 연산자는 두 | union 연산자는 두 relation튜플들의 합집합의 원소를 그 튜플로 하는 relation을 만드는 연산자이다. 이는 다음과 같이 사용한다. | ||
<math>r \smile s</math> | <math>r \smile s</math> | ||
| 70번째 줄: | 70번째 줄: | ||
[[파일:UnionOp.png|테두리|프레임없음|300x300픽셀]] | [[파일:UnionOp.png|테두리|프레임없음|300x300픽셀]] | ||
===intersection: <math>\frown</math> === | |||
union 연산자는 두 relation튜플들의 교집합의 원소를 그 튜플로 하는 relation을 만드는 연산자이다. 이는 다음과 같이 사용한다. | |||
<math>r \frown s</math> | |||
위 연산자를 사용하기 위해서는 r(R), s(S)를 만족하는 두 r, s사이에 다음이 성립해야 한다. | |||
* r, s는 반드시 arity가 동일해야 한다. (속성의 수가 같아야 한다.) | |||
* 두 attribute는 반드시 compatible해야 한다. (두 relation간의 domain이 호환되어야 한다.) | |||
이를 더 잘 이해하기 위해 다음 예시를 볼 수 있다. | |||
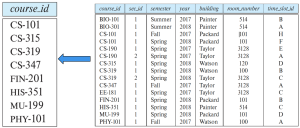
<span style="font-size: 15px;"><math>\prod_{}^{}</math></span><math>_{course\_id}(\sigma</math><sub>semester="Fall"</sub><math>_\land</math><sub> year = 2017</sub><math>(section)) \,\, \frown</math> | |||
<span style="font-size: 15px;"><math>\prod_{}^{}</math></span><math>_{course\_id}(\sigma</math><sub>semester="Spring"</sub><math>_\land</math><sub> year = 2018</sub><math>(section))</math> | |||
[[파일:IntersectionOp.jpg|테두리|프레임없음|450x450픽셀]] | |||
===set difference: - === | ===set difference: - === | ||
2025년 3월 17일 (월) 18:43 판
상위 문서: Relational Query Languages
개요
Relational algebra는 procedural 언어에 해당하며 하나 혹은 두개의 relation을 입력으로 받고 새로운 relation을 출력하는 여러 연산자로 구성된다. 이러한 Relational algebra는 SQL Query Languages의 이론적인 토대를 형성한다.
Six Basic Operator
아래에서 수식에 쓰이는 r은 relation 인스턴스를 의미한다.
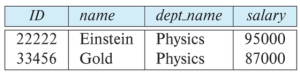
select:
위에서 select 연산은 주어진 조건(p)을 만족하는 tuple 만을 골라내어서 relation을 새로 구성한다.
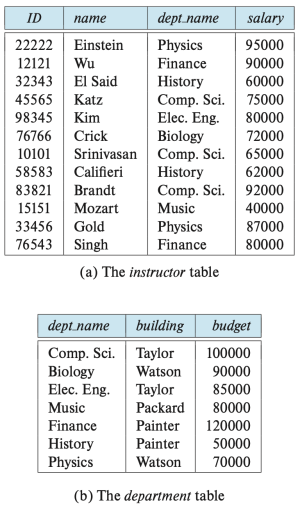
예를 들어서 "Physics" department에 속하는 instructor들이 속하는 tuple들의 relation은 다음과 같이 만들 수 있다.
- Query: dept_name = "Physics"</math>(instructor)</math>
project:
project operation은 에 속하는 속성들 만을 나타내는 k개의 column들로 이뤄진 relation을 만든다. 이때 중복되는 값이 있다면 relation은 기본적으로 집합이기 때문에 삭제된다.
예를 들어 dept_name 속성을 instructor에서 제거한 relation을 얻고 싶다면 다음과 같이 만들 수 있다.
- Query:
Cartesian-Product Operation
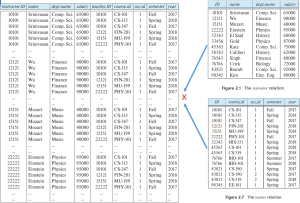
The Cartesian-product 연산자(denoted by X)는 두 relation들로부터의 정보를 섞도록 한다. 이때 우리는 결과 relation을 구성하는 tuple들을 가능한 모든 튜플들의 조합을 통해 만든다. 예를 들어 튜플의 개수가 각각 n, m인 relation A, B의 cartesian product인 A X B인 경우, A의 각 튜플들은 B의 모든 튜플들과 쌍을 이루어 n*m개의 튜플을 가지는 relation를 만든다. 다음은 instructor relation과 teaches relation간에 cartesian product 연산을 실행한 계산식과 결과의 예시이다.
instructor X teaches
Join Operation
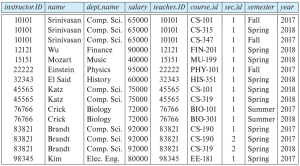
위 cartesian product 예시의 경우 instructor.ID, teaches.ID가 일치하지 않는 경우에도 하나의 튜플로 합치는 경우가 있다. 이는 필요가 없는 정보이다. 이와 같이 필요없는 튜플의 생성을 최소화하기 위한 연산자가 join 연산자이며, 이는 selection 연산자와 cartesian product 연산자의 조합으로 이루어진다. 예를 들어 instructor relation과 teaches relation간에 cartesian product 연산을 실행한 후 instructor.ID와 teaches.ID가 같은 경우의 튜플만 남기기 위해서는 다음과 같이 연산한다. 그리고 그 결과는 다음과 같다.
위에서 사용한 연산의 형식은 굉장히 자주 사용되는 형식이기에, 이를 하나의 연산자로 통합한 것이 join 연산자이다. join 연산자의 기본적인 식은 다음과 같다.
위는 A, B간의 cartesian product 연산을 실행한 후, 에 나와있는 조건(predicate)에 따라 튜플들을 select한다는 뜻이다. 즉, 이를 이용하여 위 예제의 식을 다시 표현하면 다음과 같다.
이때 join 연산자는 기본적으로 매우 큰 연산량을 필요로하는 cartesian product 연산자보다도 더욱 큰 연산량을 필요로 하므로 신중히 사용하는 것이 좋다.
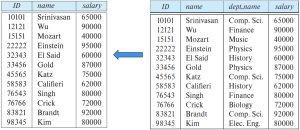
union:
union 연산자는 두 relation튜플들의 합집합의 원소를 그 튜플로 하는 relation을 만드는 연산자이다. 이는 다음과 같이 사용한다.
위 연산자를 사용하기 위해서는 r(R), s(S)를 만족하는 두 r, s사이에 다음이 성립해야 한다.
- r, s는 반드시 arity가 동일해야 한다. (속성의 수가 같아야 한다.)
- 두 attribute는 반드시 compatible해야 한다. (두 relation간의 domain이 호환되어야 한다.)
- 예를 들어, 첫 번째 컬럼이 정수형이라면 두 관계 모두 첫 번째 컬럼이 정수형이어야 한다.
이를 더 잘 이해하기 위해 다음 예시를 볼 수 있다.
semester="Fall" year = 2017 semester="Spring" year = 2018
intersection:
union 연산자는 두 relation튜플들의 교집합의 원소를 그 튜플로 하는 relation을 만드는 연산자이다. 이는 다음과 같이 사용한다.
위 연산자를 사용하기 위해서는 r(R), s(S)를 만족하는 두 r, s사이에 다음이 성립해야 한다.
- r, s는 반드시 arity가 동일해야 한다. (속성의 수가 같아야 한다.)
- 두 attribute는 반드시 compatible해야 한다. (두 relation간의 domain이 호환되어야 한다.)
이를 더 잘 이해하기 위해 다음 예시를 볼 수 있다.
semester="Fall" year = 2017 semester="Spring" year = 2018
set difference: -
cartesian product: x
rename:
Composition of Relational Operations
realtional-algebra operation의 결과는 relation이기 때문에 연산의 결과를 다른 realtional-algebra operation의 피연산자로 사용할 수 있다.
예를 들어서 physics department에 속하는 모든 instructor들의 이름을 찾는 query를 만들면 다음과 같다. namedept_name = "Physics"