Sorting Problem

상위 문서: 알고리즘 설계와 분석

개요

해당 문제는 알고리즘의 기본이라고 할 수 있는 정렬 알고리즘에 대해 다룬다. 정렬 알고리즘은 입력으로는 n개의 수 $a_1,...,a_n$으로 이루어진 수열이 주어지며, 이때 출력은 해당 수열을 재배열하여 $a{\text{'}}_1\le a{\text{'}}_2\le ...\le a{\text{'}}_n$이 되도록 하는 것이다.

Importance of Sorting

Figure 1. Difference between O(n²) and O(n log(n))

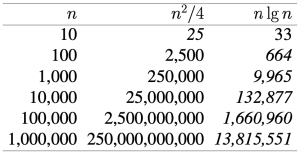
정렬은 매우 단순한 작업처럼 보이지만, 이는 실제로 매우 중요한 주제이다. 그 이유는 컴퓨터가 많은 시간을 정렬에 사용하기 때문이다. 역사적으로 컴퓨터는 약 25%의 시간을 정렬 알고리즘을 수행하는데 사용한다. 이러한 이유로, 정렬은 가장 잘 연구된 문제 중 하나이다.

컴퓨터 과학에서 정렬은 수많은 알고리즘이 연구된 주제이며, 따라서 분할 정복(divide-and-conquer), 무작위화(randomized algorithms), 시간 복잡도의 하한(lower bounds) 등과 같은 많은 개념들을 정렬 알고리즘을 공부함을 통해 배울 수 있다.

또한 데이터가 정렬되어 있으면 탐색, 중복 제거, 순위 계산, 범위 질의(range query) 등이 훨씬 쉽게 해결된다. 이때 단순한 O(n²) 정렬 알고리즘은 데이터가 커지면 사용할 수 없다. 따라서 O(n log(n)) 알고리즘을 사용해야 대규모 데이터 처리를 할 수 있다. 이는 본질적으로 시간 복잡도 측면에서 O(n²)와 O(n log(n))이 매우 큰 차이를 보이기 때문이다. Figure 1은 입력의 크기가 100,000일 때 걸리는 시간이 약 1500배나 난다는 것을 보여준다.

Pragmatics of Sorting

Comparison Functions

어떤 순열을 정렬하고자 할때, 어떤 기준으로 비교하는지는 중요한 문제이다. 예를 들어 문자열 정렬은 Alphabetizing을 기준으로 이루어 진다. 또한 그 중에서도 텍스트 문자열을 정렬할 때는 단순히 글자 순서뿐 아니라 대소문자, 구두점, 띄어쓰기 등 세부 규칙이 필요하다. 예를 들어 "Big"과 "big"을 동일시 할지 말지, 혹은 "A-B"가 "A B"보다 앞에 있을지 말지이다. 즉, 정렬이 세부적으로 어떤 기준으로 정렬할 지는 두 원소를 비교하는 함수(comparison function)에 달려 있다. 이러한 비교함수는 름차순/내림차순 여부, 대소문자 무시 여부, 사전식 정렬 여부 등을 결정한다.

Equal Elements

동일한 키를 가지는 원소들을 다룰 때에는 문제가 발생할 수 있다. 정렬 과정에서 같은 값을 가지는 원소들은 정렬 후 모두 같은 위치 근처에 위치한다. 하지만 이들의 상대적인 위치가 중요한 경우가 존재한다. 예를 들어, 한 학교 내에 있는 학생들의 성명을 성씨를 기준으로 정렬하는 경우, 성은 같더라도 이름이 다른 경우가 존재하기 때문이다. 따라서 주 키(primary key)로 구분이 안 되는 경우, 2차 키(secondary key)를 이용하여 정렬을 세밀화할 수 있다. 이는 비교 함수에서 처리되어야 한다. 이떄 퀵정렬 같은 알고리즘은 동일 원소가 많을 때 성능 저하가 생길 수 있다. 따라서 동일 원소가 많으면 특별한 처리가 필요하다.

Library Functions

우리가 프로그램을 구현할 때 정렬 기능을 이용해야 한다면, 프로그래밍 언어가 제공하는 표준 정렬 함수를 사용하는 것이 권장된다. 거의 모든 현대 프로그래밍 언어는 내장 정렬 함수를 제공한다. 이는 직접 구현하는 것보다 빠르고 안전하며, 최적화도 잘 되어 있다. 예를 들어 C언어의 qsort()는 아래와 같은 함수이다.

void qsort(void *base, size_t nel, size_t width, 
           int (*compare)(const void *, const void *));

해당 함수에서 base는 배열의 시작 주소, nel은 원소의 개수, width는 각 원소의 크기, compare는 두 원소를 비교하는 함수 포인터이다.

int intcompare(int *i, int *j) {
    if (*i > *j) return 1;
    if (*i < *j) return -1;
    return 0;
}

위는 정수 배열을 오름차순 정렬할 때 사용하는 비교 함수입니다.

Application of Sorting

정렬 문제가 수많은 사람들에 의해서 연구되고, 컴퓨터가 연산 시간의 많은 부분을 정렬에 할애하는 것은 정렬이 매우 많은 활용도를 가지기 때문이다. 해당 문단에서는 정렬이 응용이 되는 중요한 몇 가지 방식에 대해 설명한다.

Searching

정렬의 가장 대표적인 응용은 이진 탐색(Binary Search)이다. 이진 탐색은 정렬된 배열에서 어떤 원소가 있는지 검사할 때, O(log n) 시간에 가능하게 한다. 데이터가 정렬되어 있지 않으면 O(n)의 시간 복잡도를 가지는 선형 탐색밖에 못 하므로, 정렬 후 탐색하는 것이 훨씬 효율적이다. 따라서 "탐색 전처리(Search preprocessing)”은 정렬의 가장 중요한 응용 중 하나이다.

Closest Pair

Closest Pair 문제는 n개의 숫자가 주어졌을 때, 서로 가장 가까운 두 수를 찾는 것이다. 정렬하지 않은 경우, O(n²)의 시간 복잡도 동안 모든 쌍을 비교해야 한다. 이때 가장 가까운 쌍은 정렬된 배열에서 인접한 두 원소 중에 반드시 존재한다. 이러한 사실을 이용하면, Closest Pair 문제는 전체를 정렬한 뒤 O(n)의 시간 복잡도 동안 한 번만 선형 스캔하면 해결된다. 따라서 Closest Pair 문제의 시간 복잡도는 아래와 같이 계산 된다:

$O(nlog(n))$(정렬) + $O(n)$(선형 검사) = $O(nlog(n))$

Element Uniqueness

Element Uniqueness 문제는 n개의 원소가 주어졌을 때, 모두 다른 값인지 아니면 중복된 값이 있는지 확인하는 문제이다. 배열을 정렬하면, 동일한 값들은 반드시 연속해서 나타나므로, 따라서 정렬 후 선형 스캔을 하면서 인접한 원소가 같은지만 확인하면 된다. 사실상 사실상 “Closest Pair” 문제의 특수한 경우이다.

Mode

최빈값(Mode) 문제는 n개의 아이템 중 가장 많이 등장하는 원소를 찾는 문제이다. 배열을 정렬하면 동일한 값들이 연속해서 나타난다. 이에 따라 해당 문제를 해결하기 위해서는, 선형 스캔을 하며 “같은 값이 몇 번 연속하는지(run length)”를 세어 최댓값을 찾으면 된다. 즉, 인접 구간들의 길이를 비교하면 최빈값을 알 수 있다.

이때 어떤 원소 k가 몇 번 나타나는지 확인하려면, O(log(n))의 이진 탐색으로 k−ϵ과 k+ϵ의 위치를 찾은 뒤, 그 구간 길이를 계산할 수 있다. 어찌 되었건 간에, 시간 복잡도는

$O(nlog(n))$(정렬) + $O(n)$(스캔) = $O(nlog(n))$

Median and Selection

Selection 문제는 집합에서 k번째로 큰 원소를 찾는 것이다. 이때 중간값(median)은 k를 n/2로 설정하여 구할 수 있다. 해당 문제도 정렬을 활용하면 간단하다. 배열을 정렬하면, k번째 원소를 한 번의 인덱싱으로 O(1)에 찾을 수 있기 때문이다. 따라서 해당 방법의 시간 복잡도는 O(n log(n))이다. 실제로는 "Median of Medians" 알고리즘 같은 특별한 방법으로 O(n)에 중간값을 구할 수 있지만, 아이디어는 여전히 "부분 정렬(partial sorting)"과 관련이 있다.

Finding Convex Hulls

Figure 2. Finding Convex Hull

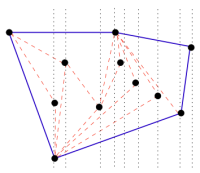
Finding Convex Hulls 문제는 2차원 평면 위에 n개의 점이 주어졌을 때, 이 모든 점을 내부 혹은 껍질(hull)에 포함하는 가장 작은 볼록 다각형(convex polygon)을 찾는 문제이다. 직관적으로는 Figure 2와 같이 볼록 껍질을 찾는다는 것은 고무 밴드를 점들을 둘러싸듯이 잡아당겼을 때 생기는 외곽선을 찾는 것과 같다. 이는 컴퓨터 기하학(Computational Geometry)의 기본 문제 중 하나이며, 더 복잡한 알고리즘(최근접 점 문제, Voronoi diagram 등)의 기본 원형이다. 이를 해결하기 위해서는 아래와 같은 방법을 채택할 수 있다:

1. 점들을 x좌표 기준으로 정렬한다.
2. 왼쪽에서 오른쪽으로 점들을 추가하며 현재 껍질(hull)을 갱신한다.
3. 이때 오른쪽 끝 점은 항상 껍질의 일부이므로, 순차적으로 추가하며 안쪽에 들어가는 점들을 제거한다.

해당 알고리즘에서 정렬의 역할은 점들을 미리 정렬하여 매번 모든 점이 껍질 안에 있는지 검사할 필요가 없도록 하는 것이다. 또한 새로운 점을 추가할 때 껍질에 영향을 주는지 효율적으로 판정할 수 있다. 따라서 정렬 후, 선형 시간에 껍질을 구축할 수 있으므로 해당 알고리즘의 시간 복잡도는 O(n log(n))이다.

Selection Sort

선택 정렬(Selection Sort) 알고리즘은 배열 전체를 여러 번 훑으면서, 그 중에서 가장 작은 원소를 찾아 앞으로 옮기는 방식으로 작동한다. 이를 C언어 코드로 표현하면 아래와 같다:

void selection_sort(item_type s[], int n) {
    int i, j;   /* counters */
    int min;    /* index of minimum */
    for (i = 0; i < n; i++) {
        min = i;
        for (j = i + 1; j < n; j++) {
            if (s[j] < s[min]) {
                min = j;
            }
        }
        swap(&s[i], &s[min]);
    }
}

위 알고리즘에서 바깥쪽 for 루프는 n번 돈다. 안쪽의 루프는 바깥 루프의 인덱스가 i일 때, n−(i+1)번 돈다. 이에 따라 if 문이 실행되는 정확한 횟수는 아래와 같다.

$T(n)=\sum _{i=0}^{n-1}\sum _{j=i+1}^{n-1}1=\sum _{i=0}^{n-1}(n-i-1)=\sum _{i=0}^{n-1}i$
$\therefore T(n)=(n-1)+(n-2)+(n-3)+\cdots +2+1$

따라서 최악의 경우(worst case) 해당 알고리즘의 시간 복잡도는 $\mathrm{\Theta }(n^2)$이다. 하지만 이 방식은 조금 지루하고 까다로운 방식이다. 빅 오 표기법은 오직 최대 차항의 차수에만 신경을 쓰면 되기 때문에, 바깥쪽의 루프는 n번, 안쪽의 루프도 최대 n번 돌기 때문에, 선택 정렬(selection sort)은 최악의 경우 $n\times n=O(n^2)$ 시간이 걸린다는 것을 어렵지 않게 추론할 수 있다. 이때 해당 알고리즘은 이미 정렬돼 있든(최선), 완전히 역순이든(최악) 상관없이, 비교 횟수는 동일하므로, $\mathrm{\Theta }(n^2)$임을 추론할 수 있다.

Insertion Sort

삽입 정렬(Insertion Sort)은 배열의 앞 부분이 이미 정렬되어 있다고 가정하고, 뒤에서 새 원소를 하나씩 꺼내어 알맞은 위치에 삽입하며 전체를 정렬하는 알고리즘이다. 이를 C 언어 코드로 표현하면 아래와 같다:

void insertion_sort(item_type s[], int n) {
    for (i = 1; i < n; i++) {
        j = i; //이번에 삽입할 원소
        while ((j > 0) && (s[j] < s[j - 1])) { //s[j]가 올바른 위치에 있으면 while문 종료
            swap(&s[j], &s[j - 1]); //그렇지 않으면 스왑
            j = j - 1;
        }
    }
}

위의 코드의 시간 복잡도를 추론하기 위해서는 내부 while 루프가 얼마나 도는지를 알아야 한다. 최악의 경우에 대해서 고려한다면, 내부의 while 문은 항상 i번 돈다고 할 수 있다. 이때 i < n이고 바깥 while문은 n번 도므로, 삽입 정렬의 시간 복잡도는 $O(n^2)$이다.

Heap Sort

Selection sort 알고리즘은 더욱 효율적인 데이터 구조를 사용하여 개선할 수 있다. 먼저, selection sort는 아래와 같은 흐름을 가진다:

• for i = 1 to n : 배열의 크기 n에 대해, i번째 위치에 들어갈 원소를 선택하는 과정을 반복한다.
  1. A 단계: 남아 있는 원소들 중에서 가장 작은 값을 찾는다. 남아 있는 원소의 개수는 n - i + 1이다.
  2. B 단계: 찾은 최소값을 배열에서 꺼내어 앞으로(즉, i번째 자리)에 둔다.

이때 A, B 단계의 시간 복잡도를 각각 T(A), T(B)라고 하면, 전체 알고리즘의 시간 복잡도는 O(n(T(A)+T(B)))이다. 이때 우리는 시간 복잡도 T(A) = O(n²)를 개선할 수 있다. 그 방법은 Heap과 같은 자료구조를 사용하여, 최소(최대) 원소에 대한 접근의 시간 복잡도를 O(n)이 아닌 O(log(n))이 걸리도록 하는 것이다. 이는 아래와 같은 구조를 가지는 알고리즘이다:

1. Heapify로 배열을 힙으로 만든 뒤, → O(n)
2. extract_min(또는 extract_max)을 반복해서 정렬한다. → O(n log(n))

void heapsort_(item_type s[], int n) {
    int i;
    priority_queue q;
    make_heap(&q, s, n);          // 배열을 힙으로 변환
    for (i = 0; i < n; i++) {
        s[i] = extract_min(&q);   // 매번 최소값 꺼내어 배열에 저장
    }
}

Merge Sort

Merge sort는 재귀적인 알고리즘으로, 큰 문제를 작은 문제로 나누어 해결하는 방식을 취한다. 이는 배열을 두 그룹으로 나눈 뒤, 각각을 재귀적으로 정렬하고, 마지막에 두 정렬된 리스트를 합쳐서 최종적으로 정렬된 리스트를 얻는 방법이다. 이는 “Divide and Conquer(분할 정복)”이라는 알고리즘 개념의 전형적인 예시이다. 아래는 merge sort를 구현한 코드이다:

// 인자: s는 배열, low와 high는 정렬 구간의 시작과 끝 인덱스
void mergesort_(item_type s[], int low, int high) {
    int middle;
    if (low < high) {
        middle = (low + high) / 2; // 배열을 두 구간으로 나눔
        // 왼쪽 구간(low ~ middle)과 오른쪽 구간(middle+1 ~ high)을 재귀적으로 정렬
        mergesort_(s, low, middle); 
        mergesort_(s, middle + 1, high);
        merge(s, low, middle, high); //merge() 함수로 두 구간을 합병
    }
}

Merge sort의 핵심적인 성능은 두 개의 정렬된 리스트를 얼마나 효율적으로 합치는가에 달려 있다. 이때 합치는 과정은, 가장 작은 원소를 두 리스트의 맨 앞에서 비교해 하나씩 빼내고, 그 과정을 반복하는 것이다. 예를 들어, 두 리스트 A = {5,7,12,19}, B = {4,6,13,15}를 합칠 경우:

1. 먼저 4 vs 5 비교 → 4 선택
2. 5 vs 6 비교 → 5 선택
3. 6 vs 7 비교 → 6 선택
4. 이런 식으로 n-1번 비교, 즉 O(n) 시간에 합칠 수 있다.

이를 구현하기 위해서 코드로 나타내면 아래와 같다:

void merge(item_type s[], int low, int middle, int high) {
    int i;
    queue buffer1, buffer2;
    init_queue(&buffer1);
    init_queue(&buffer2);

    // 왼쪽, 오른쪽 구간의 데이터를 각각 큐에 저장
    for (i = low; i <= middle; i++) enqueue(&buffer1, s[i]);
    for (i = middle + 1; i <= high; i++) enqueue(&buffer2, s[i]);

    i = low;
    // 두 큐가 비어있지 않은 동안 앞 원소를 비교
    while (!(empty_queue(&buffer1)) || empty_queue(&buffer2)) {
        if (headq(&buffer1) <= headq(&buffer2))
            s[i++] = dequeue(&buffer1);
        else
            s[i++] = dequeue(&buffer2);
    }

    // 남은 원소들 처리
    while (!empty_queue(&buffer1)) s[i++] = dequeue(&buffer1);
    while (!empty_queue(&buffer2)) s[i++] = dequeue(&buffer2);
}