Robot Tour Optimization: 두 판 사이의 차이
편집 요약 없음 |
|||
| 19번째 줄: | 19번째 줄: | ||
Visit <math>p_i</math> | Visit <math>p_i</math> | ||
Return to <math>p_0</math> from <math>p_i</math> | Return to <math>p_0</math> from <math>p_i</math> | ||
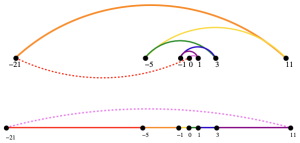
하지만 이러한 단순한 접근법은 틀렸다. Figure 1은 이를 증명하는 반례이다. | 하지만 이러한 단순한 접근법은 틀렸다. Figure 1은 이를 증명하는 반례이다. | ||
===Closest Pair Tour=== | |||
해당 알고리즘은 체인(chain)이라는 개념을 사용한다. 체인은 연결된 점들의 경로를 의미하여, 시작과 끝에 끝점(endpoint)이 존재한다. 이때 알고리즘의 처음에는 모든 점은 길이가 0인 체인으로 간주된다. 알고리즘의 매 단계 마다 서로 다른 체인에 속한 끝점 들 중, 가장 가까운 쌍을 골라서 연결한다. 이때 주의해야 할 것은 모든 점이 하나의 체인으로 합쳐지기 전까지는 체인의 양 끝점이 연결되어 해당 알고리즘이 조기 종료되지 않도록 하는 것이다. 만약 하나의 체인에 모든 점이 속한다면, 해당 체인의 양 끝점을 서로 연결하여 사이클을 종료한다. 이는 아래와 같은 수도 코드를 따른다. | |||
Let <math>n</math> be the number of points in the set | |||
For <math>i = 1</math> to <math>n - 1</math> do | |||
<math>d=\infty</math> | |||
For each pair of endpoints <math>(x, y)</math> of partial paths | |||
If <math>dist(x, y) \le d</math> then | |||
<math>x_m =x,y_m =y,d=dist(x,y)</math> | |||
Connect <math>(x_m, y_m)</math> by an edge | |||
Connect the two endpoints by an edge. | |||
==각주== | ==각주== | ||
2025년 9월 4일 (목) 01:59 판
개요
Robot Tour Optimization 문제란, 어떠한 공장에서 납땜 인두와 같은 도구가 장착된 로봇팔이 주어졌을 때, 회로 기판을 제조할 때는 모든 칩과 다른 부품들을 기판에 고정하기 위해서 취해야 하는 가장 효율적인 동선을 찾는 것이다. 더 구체적으로, 각 칩에는 보드에 납땜되어야 하는 접점들의 집합이 있다. 이 작업을 위해 로봇 팔을 프로그래밍하려면, 로봇이 첫 번째 접점을 방문(그리고 납땜)하고, 그다음 두 번째, 세 번째 접점을 방문하는 식으로 작업이 끝날 때까지 동선을 구성해야 하며, 또한 모든 작업을 마친 후에는 다음 보드를 준비하기 위해서 첫 번째 접점으로 되돌아가므로, 로봇팔의 동선은 닫힌 순회 동선이 된다. 이때 두 점 사이를 이동하는 시간은 그 거리와 비례한다. 따라서 요약하자면 아래와 같은 알고리즘 문제이다.
입력: 평면 위의 n개 점으로 이루어진 집합 S. 출력: 집합 S의 각 점을 방문하는 가장 짧은 닫힌 순회 동선은 무엇인가?
알고리즘
Nearest Neighbor Tour
해당 문제에 대해 가장 쉽게 취할 수 있는 접근법은 현재 로봇팔이 위치한 접점에서 가장 가까이에 위치한 접점을 다음 접점으로 선택하는 것이다. 이는 아래와 같은 수도 코드(pseudo code)를 통해서 나타낼 수 있다.
Pick and visit an initial point
While there are still unvisited points
Let be the closest unvisited point to
Visit
Return to from
하지만 이러한 단순한 접근법은 틀렸다. Figure 1은 이를 증명하는 반례이다.
Closest Pair Tour
해당 알고리즘은 체인(chain)이라는 개념을 사용한다. 체인은 연결된 점들의 경로를 의미하여, 시작과 끝에 끝점(endpoint)이 존재한다. 이때 알고리즘의 처음에는 모든 점은 길이가 0인 체인으로 간주된다. 알고리즘의 매 단계 마다 서로 다른 체인에 속한 끝점 들 중, 가장 가까운 쌍을 골라서 연결한다. 이때 주의해야 할 것은 모든 점이 하나의 체인으로 합쳐지기 전까지는 체인의 양 끝점이 연결되어 해당 알고리즘이 조기 종료되지 않도록 하는 것이다. 만약 하나의 체인에 모든 점이 속한다면, 해당 체인의 양 끝점을 서로 연결하여 사이클을 종료한다. 이는 아래와 같은 수도 코드를 따른다.
Let be the number of points in the set
For to do
For each pair of endpoints of partial paths
If then
Connect by an edge
Connect the two endpoints by an edge.