Relational Database Design

상위 문서: 데이터베이스 시스템

개요

Figure 1. Database schema for the university example

Figure 2. The in_dep relation

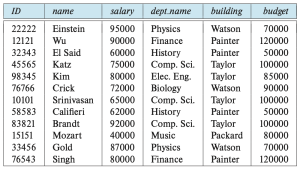
해당 문서와 그 하위 문서에서는 relational 데이터베이스(database)를 위한 스키마(schema)를 설계하는 방법에 대해 다룬다. 일반적으로 relational 데이터베이스를 설계할 때 중요한 것은 불필요한 중복(redundancy)없이 정보를 저장하면서도, 정보를쉽게 검색할 수 있도록 하는 어떤 relation 스키마를 생성하는 것이다. 이는 적절한 정규형(normal form)에 해당하는 스키마를 설계하여 달성할 수 있다. 해당 문서와 그 하위 문서에서 사용하는 대학교의 데이터베이스의 스키마들은 figure 1과 같다.

Features of Good Relational Designs

E-R 모델 설계로 부터 직접 relation 스키마 집합을 생성하는 것이 가능하며, 생성된 relation 스키마 집합의 좋고 나쁨은 기반이 된 E-R 모델의 설계가 얼마나 잘 되었는지에 의해 결정된다. 예를 들어 대학교 엔터프라이즈를 설계할 때, 다음과 같은 스키마로 시작했다고 가정하자.

in_dep (ID, name, salary, dept_name, building, budget)

해당 스키마는 instructor(교수)와 department(학과)에 해당하는 릴레이션 간의 natural join의 결과이다. 이 스키마는 어떤 쿼리에 대해 더 간단히 표현할 수 있기 때문에 좋은 스키마처럼 보일 수 있다. 하지만 이는 문제를 가지고 있다. 이는 figure 2에 제시된 인스턴스에서, 각 학과에 속한 교수마다 학과 정보를 반복해서 저장해야 한다는 것이다. 즉, 불필요한 중복이 스키마 인스턴스에 나타난다. 이는 해당하는 모든 중복되는 튜플의 속성들의 값이 모두 일치해야 하며, 그렇지 않다면 일관성(cinsistency)를 잃게 된다.
또한 in_dep 스키마에는 여전히 다른 문제가 존재한다. 새로운 학과(department)를 생성할 경우, 위의 스키마를 이용한다면 해당 학과에 속한 교수(ID, name, salary)가 적어도 한 명 있어야만 학과에 해당하는 정보(dept_name, building, budget)를 비로소 담을 수 있다.

Decomposition

위의 in_dep 스키마에서 정보 반복 문제(repetition-of-information problem) 를 피할 수 있는 유일한 방법은, 이를 두 개의 스키마로 분해(decompose) 하는 것이다. 이 경우에는 instructor 스키마와 department 스키마로 분해한다. 일반적으로 정보가 반복되는 스키마는 여러 개의 더 작은 스키마로 분해해야 한다.

Figure 3. Loss of information via a bad decomposition

하지만 모든 분해가 바람직한 것은 아니다. 예를 들어,

employee (ID, name, street, city, salary)

와 같은 스키마를 다음과 같이 분해한다고 가정하자:

employee1 (ID, name)
employee2 (name, street, city, salary)

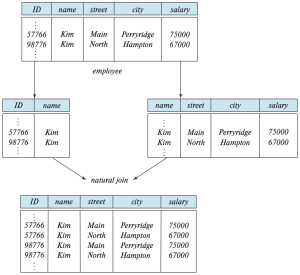
해당 분해가 좋지 않은 이유는, 어떤 기업(enterprise) 내에 이름이 같지만 서로 다른 두 명의 직원이 동명이인으로 존재할 수 있기 때문이다. 예를 들어, 대학에 이름이 Kim인 두 명의 직원이 있다고 가정하면 원래의 employee 스키마에 대해 이 두 직원은 다음과 같은 튜플을 가진다:

(57766, Kim, Main, Perryridge, 75000)
(98776, Kim, North, Hampton, 67000)

Figure 3는 위의 원래 튜플과, 원래의 스키마를 분해하여 생성한 스키마를 이용한 튜플들, 해당 스키마들로부터 natural join를 통해 원래의 튜플을 복구하기 위해 시도한 결과를 보여준다. Figure 3에서 알 수 있듯이, 원래의 두 튜플은 물론 이름이 Kim인 두 직원의 데이터를 잘못 조합한 두개의 새로운 튜플도 나타난다. 이는 사실상 정보가 손실된 것이다. 그 이유는 어느 Kim이 어떤 거리(street), 도시(city), 급여(salary) 속성 값을 가지는지 구별할 수 없기 때문이다. 이렇게 분해할 경우 정보가 손실되는 분해를 손실 분해(lossy decomposition) 라고 부르고, 반대로 정보 손실 없이 분해할 수 있는 경우를 손실 없는 분해(lossless decomposition)라고 한다.

Lossless Decomposition

R이 하나의 relation 스키마이고, R1과 R2가 R을 분해하여 형성된 스키마라고 할 때, R, R1, R2를 속성들의 집합이라고 하면 $R=R1\cup R2$와 같이 나타낼 수 있다. 이때 R을 두 개의 릴레이션 스키마 R1과 R2로 대체했을 때 정보 손실이 없다면, 이 분해를 손실 없는 분해(lossless decomposition)라고 한다. 정보 손실(loss of information) 은, 어떤 경우에 r(R)의 인스턴스(instance)를 가지고 있을 때, r(R)의 인스턴스 대신 r1(R1)과 r2(R2)의 인스턴스를 사용하면 표현할 수 없는 정보가 생기는 경우 발생한다.

Figure 4. Example of Lossless Decomposition

더 정확하게는 R에 대한 인스턴스 r이 다음 SQL 쿼리의 결과와 같은 튜플 집합을 가진다면 손실 없는 분해이다:

select *
from (select R1 from r) natural join (select R2 from r)

이를 relational algebra로 표현하면 다음과 같다:

$\prod _{R1}(r)\bowtie \prod _{R2}(r)=r$

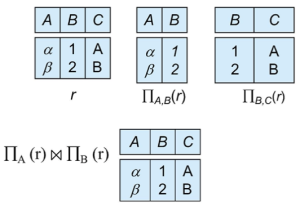
즉, 인스턴스 r을 각각 R1, R2에 대해 projection를 수행한 결과에 대해 natural join을 수행하면, 정확히 r을 다시 얻을 수 있어야 한다. 손실 없는 분해의 예시는 figure 4에서 잘 나타나있다. <code>R1 =(A,B)</code>, <code>R2 =(B,C)</code>는 해당 과정을 수행할 경우, 원래의 인스턴스 r을 반환한다.

반대로, 손실 분해(lossy decomposition)의 경우는, projection를 수행한 결과에 대해 natural join을 수행하면 원래 릴레이션보다 더 큰 집합(proper superset)이 나오는 경우이다. 이를 relational algebra로 표현하면 다음과 같다:

$r\subset \prod _{R1}(r)\bowtie \prod _{R2}(r)$

Normalization Theory

"좋은 형태" 에 있는 어떤 스키마 집합을 도출하기 위해서는 정규환 이론(Normalization Theory)을 사용하여야 한다. 이때 "좋은 형태"란 정보 반복 문제가 없는 형태이다. "좋은 형태"에 있는 relational 데이터베이스를 설계하기 위해서는 일반적으로 정규화(normalization)이라고 알려진 방법을 사용해야 한다.

정규화의 목표는 불필요한 중복 없이 정보를 저장할 수 있고 정보를 쉽게 검색할 수 있도록 하는 어떤 relation 스키마 집합을 생성하는 것이다. 이를 위해서는 다음의 접근 방법이 사용된다.

• 주어진 릴레이션 스키마가 "좋은 형태"에 있는지를 결정한다.
• 주어진 relation 스키마가 "좋은 형태"가 아닌 경우, 해당 스키마를 여러 개의 더 작은 relation 스키마로 분해한다.

이때 relation 스키마가 정규형 중 하나에 속하는지 판단하기 위해서는 함수 종속성(functional dependancy)를 사용해야 한다.

Functional dependencies

데이터베이스는 현실 세계에서의 엔터티(entities)와 관계(relationships) 집합을 모델링한다. 이때, 현실 세계의 데이터에는 보통 다양한 제약 조건(constraints)이 존재한다. 예를 들어, 대학교의 데이터베이스에서 기대되는 몇 가지 제약 조건은 다음과 같다:

• 학생과 교수는 각각 ID에 의해 고유하게 식별된다.
• 각 학생과 교수는 단 하나의 이름(name) 만을 가진다.(sigle-valued)
• 각 교수와 학생은(주로) 단 하나의 학과에만 소속된다.
• 각 학과는 단 하나의 예산(budget) 값과, 단 하나의 연관된 건물(building)을 가진다.

이러한 모든 현실 세계의 제약 조건을 만족하는 릴레이션의 인스턴스를 합법적 인스턴스(legal instance) 라고 부른다. 모든 릴레이션 인스턴스가 합법적 인스턴스인 경우, 해당 데이터베이스 인스턴스를 합법적 데이터베이스 인스턴스(legal instance of a database)라고 한다.

Notational Conventional

일반적으로 relation schema를 설계할 때 사용되는 표기 규약은 아래와 같다:

• 일반적으로
  • 속성 집합을 표현할 때는 그리스 문자(예:α)를 사용한다.
  • 릴레이션 스키마를 나타낼 때는 대문자 로마자(예:R) 를 사용한다.
  • r(R)이라는 표기법을 사용하여 릴레이션 r이 스키마 R을 가진다는 것을 나타낸다.
• 릴레이션 스키마는 속성들의 집합이지만, 모든 속성 집합이 스키마인 것은 아니다.
  • 우리가 소문자 그리스 문자를 사용할 때는, 그것이 스키마일 수도 있고 아닐 수도 있는 단순한 속성 집합을 의미한다.
  • 반면, 로마자를 사용할 때는, 해당 속성 집합이 확실히 스키마임을 나타내고자 할 때 사용한다.
• 속성 집합이 슈퍼키(superkey) 인 경우, 우리는 이를 K로 나타낼 수 있다.
• 릴레이션 이름은 소문자 로마자(예:r)를 사용한다.
• 릴레이션은 주어진 시점에서 특정한 값을 가지며, 이를 인스턴스(instance)라고 한다.
  • "r의 인스턴스"라는 표현을 사용하며, 문맥상 인스턴스라는 것이 명확할 때는 단순히 릴레이션 이름(예:r)만을 사용할 수 있다.

Keys and Functional Dependencies

현실 세계(real world)에서 흔히 사용되는 제약 조건(constraints) 유형 중 많은 것은 슈퍼키(superkey), 후보키(candidate key), 기본키(primary key) 또는 함수 종속성(functional dependency)이다.

예를 들어, 슈퍼키가 전체 튜플을 고유하게 식별하는 속성 집합이라면, 함수 종속성(functional dependency)은 특정 속성들의 값을 고유하게 식별하는 제약 조건을 표현할 수 있다. r(R)이라는 릴레이션 스키마가 주어지고, α ⊆ R, β ⊆ R이라 하자.

• r(R)의 인스턴스가 주어졌을 때, 모든 튜플 쌍 t1, t2에 대해, 만약 t1[α] = t2[α]이면, 항상 t1[β] = t2[β]가 성립하는 경우, 우리는 그 인스턴스가 함수 종속성 α → β를 만족(holds on)한다고 한다.
• 스키마 r(R)의 모든 합법적인 인스턴스가 α → β를 만족한다면, 우리는 함수 종속성 α → β가 스키마 r(R)에서 성립(holds on)한다고 말한다.

함수 종속성 표기법을 사용하여, K → R이 r(R)에서 성립하면, K는 r(R)의 슈퍼키라고 할 수 있다. 즉, r(R)의 모든 합법적 인스턴스에서, 모든 튜플 쌍 t1, t2에 대해 t1[K] = t2[K]이면, t1[R] = t2[R] (즉, t1 = t2)가 되어야 한다. 함수 종속성은 슈퍼키만으로는 표현할 수 없는 제약 조건도 표현할 수 있다. 예를 들어, 해당 문서에서 이미 다룬 스키마:

in_dep (ID, name, salary, dept_name, building, budget)

여기서 dept_name → budget 이라는 함수 종속성이 성립하는데, 그 이유는, 각 학과(department)는 고유한 예산(budget) 값을 가지기 때문이다. (ID, dept_name) 쌍이 in_dep 스키마의 슈퍼키라는 것은 다음과 같이 표현할 수 있다:

ID, dept_name → other attributes

Use of Functional Dependencies

함수 종속성은 다음 두가지 방법으로 사용된다.

1. 어떤 릴레이션 인스턴스가 주어진 함수 종속성 집합 F를 만족(satisfies)하는지 검사하기 위해서
   • 만약 r이 함수 종속성 집합 F에 대해서 합법적이라면, r이 F를 만족(satisfies)한다고 한다.
2. 허용 가능한 릴레이션 집합에 대해 제약 조건을 명시하기 위해.
   • 즉 r(R)라는 스키마에서 어떤 함수 종속성 집합 F가 성립(holds on)한다고 할 때는 r(R)에 대한 모든 합법적인 인스턴스가 F를 만족(satisfies)해야 한다.

Figure 5. Sample instance of relation r

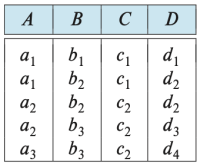
Figure 5를 통해서 함수 종속성이 어떻게 이뤄지는지 잘 살펴볼 수 있다:

1. A → C 함수 종속성은 만족된다.
   • a1이라는 A 값을 가진 두 튜플은 모두 같은 C 값 c1을 가진다.
   • a2라는 A 값을 가진 두 튜플도 같은 C 값 c2를 가진다.
   • A 값이 같은 다른 튜플 쌍은 존재하지 않는다.
2. 반면, C → A는 만족되지 않는다.
   • 튜플 t1 = (a2, b3, c2, d3)와 튜플 t2 = (a3, b3, c2, d4)를 살펴보면 두 튜플은 C 값 c2는 같지만, A 값은 a2와 a3로 다르다.
   • 즉, t1[C] = t2[C]인데도 t1[A] ≠ t2[A]이다. 따라서 C → A는 성립하지 않는다.

Trivial Functional Dependencies

일부 함수 종속성은 자명하다(trivial)고 불린다. 왜냐하면, 모든 릴레이션에서 항상 만족되기 때문이다.

• 예를 들어:
  • A → A는 항상 만족된다. 모든 튜플 쌍 t1, t2에 대해, t1[A] = t2[A]이면, 당연히 t1[A] = t2[A]이기 때문이다.
  • AB → A도 항상 만족된다.

일반적으로, 어떤 함수 종속성 α → β가 데이터베이스에 대한 제약 조건으로 주어졌을 때, α ⊆ R, β ⊆ R을 만족하는 모든 스키마 R에 대해 항상 α → β가 성립해야 한다.

Closure of a Set of Functional Dependencies

주어진 함수 종속성 집합 F가 릴레이션 r(R)에서 성립할 때, 다른 함수 종속성들이 추가로 유도될 수도 있다. 예를 들어 r(A, B, C) 스키마에서, A → B, B → C가 성립하면 A → C도 성립한다고 추론할 수 있다. 왜냐하면 A 값이 주어지면 B 값이 하나로 정해지고, 그 B 값으로부터 다시 C 값이 하나로 정해지기 때문이다. 이렇게 F로부터 유도될 수 있는 모든 함수 종속성들의 집합을 F의 폐포(closure)라고 하며, F⁺와 같이 표현한다. 이때, F⁺는 당연히 F 내의 함수 종속성들도 포함한다.

Lossless Decomposition

함수 종속성(functional dependency) 을 사용하여 어떤 분해가 손실 없는 분해(lossless decomposition) 인지를 판별할 수 있다. R, R1, R2, 그리고 F가 위에서 정의된 것처럼 주어졌다고 하자. 이때, R1과 R2가 R의 손실 없는 분해를 형성하는 조건은 다음 둘 중 하나가 F⁺(F의 폐포) 안에 존재하는 경우이다:

• R1 ∩ R2 → R1
• R1 ∩ R2 → R2

R1과 R2의 공통 속성의 집합(R1 ∩ R2)이 R1 또는 R2 중 하나에 대한 슈퍼키가 되면 그 분해는 손실 없는 분해가 된다.

예를 들어 R = (A, B, C)과 같이 R이라는 스키마가 A, B, C 세개의 속성으로 이루어져 있고, F = {A → B, B → C}와 같이 함수 종속성 집합 F가 주어졌다고 가정하자:

• 이때, R₁ = (A, B), R₂ = (B, C)는 손실없는 분해이다.
  • R₁ ∩ R₂ = {B}이므로 공통 속성은 B 하나 뿐이다.
  • 주어진 F에는 B → C가 있고, R₂는 (B, C)이므로 B만 알면 C도 알 수 있으니까 R₂를 완전히 결정할 수 있다.
• 그리고, R₁ = (A, B), R₂ = (A, C)는 손실없는 분해이다.
  • R₁ ∩ R₂ = {A}이므로 공통 속성은 A 하나 뿐이다.
  • 주어진 F에는 A → B가 있고, R₁은 (A, B)이므로 A만 알면 B도 알 수 있으니까 R₁을 완전히 결정할 수 있다.

Normal Forms

자세한 내용은 Normal Forms 문서를 참조하십시오.

Functional-Dependency Theory

해당 문단에서는 주어진 함수 종속성 집합에서 어떠한 함수 종속성들이 논리적으로 추론 가능한지 설명하는 이론에 대해 살펴본다.

Closure of a Set of Functional Dependencies

어떤 스키마에 대해 함수 종속성 집합 F가 존재할 때, 그에 따라 성립하는 다른 함수 종속성들을 논리적으로 추론가능하다(logically implied)된다고 한다. 좀더 형식적으로 말하면, relational 스키마 r(R)가 있고, 함수 종속성 f가 R에 대해 존재할 때, 모든 r(R) 인스턴스가 F를 만족한다면 f도 반드시 만족하는 경우, 우리는 f가 F로부터 논리적으로 추론 가능하다(logically implied)고 한다. 따라서 정규형을 테스트할 때에는 단순히 주어진 함수 종속성만을 고려하는 것이 아니라, 스키마에서 성립하는 모든 함수 종속성들을 고려해야 한다.

예를 들어, 관계 스키마 r과 그 함수 종속성이 아래와 같이 정의되어 있다고 하자.

r(A,B,C,G,H,I)
A→B
A→C
CG→H
CG→I
B→H

이때 함수 종속성 A → H는 논리적으로 추론 가능하다. 즉, 주어진 함수 종속성을 만족하는 모든 relational 인스턴스는 반드시 A → H를 만족한다. 이는 아래와 같이 증명된다:

두 튜플 t1​, t2​가 t1[A]=t2[A]일 때,
A → B 이므로 t1[B]=t2[B]
B → H 이므로 t1[H]=t2[H]

따라서 t1[A]=t2[A]이면, t1[H]=t2[H]이다. 즉, A → H의 정의와 같다.

Armstrong’s Axioms

함수 종속성 집합 F가 있을 때, F⁺는 F로 부터 논리적으로 추론 가능한 모든 함수 종속성들의 집합이다. 이론적으로는 F의 정의를 통해서 직접 F⁺를 계산할 수 있음에도, F가 커짐에 따라 그 과정이 기하급수적으로 복잡해질 수 있다. 따라서 위의 A → H의 증명과 같이 직접 증명하는 방식은 비효율 적이고, 함수 종속성의 추론을 단순화하는 공리(axioms)들이 사용된다. 아래 공리들에서 그리스 문자(예:α, β)는 속성 집합, 로마 대문자(예: A, B)는 개별 속성을 나타낸다. 또한 αβ는 α ∪ β를 의미한다. 아래는 Armstrong의 공리이다:

1. Reflexivity Rule: β ⊆ α이면, α → β
2. Augmentation Rule: α → β이면, γα → γβ
3. Transitivity Rule: α → β, β → γ이면, α → γ

이 공리들은 sound하고, complete하다. 또한, 아래는 Armstrong 공리로부터 유도 가능한 규칙들이다:

1. Union Rule: α → β, α → γ 이면, α → βγ
2. Decomposition Rule: α → βγ 이면, α → β, α → γ
3. Pseudotransitivity Rule: α → β, γβ → δ 이면, αγ → δ

이를 위의 예제에 적용하면 아래의 추가적인 함수 종속성들을 구할 수 있다:

A → H: A → B, B → H, Transitivity Rule 사용
CG → HI: CG → H, CG → I, Union Rule 사용
AG → I: A → C, CG → I, Pseudotransitivity Rule 사용

아래는 F⁺을 계산하는 알고리즘이다:

F⁺ = F
apply the reflexivity rule /* Generates all trivial dependencies */
repeat
    for each functional dependency f in F⁺
        apply the augmentation rule on f
        add the resulting functional dependencies to F⁺
    for each pair of functional dependencies f₁ and f₂ in F⁺
        if f₁ and f₂ can be combined using transitivity
            add the resulting functional dependency to F⁺
until F⁺ does not change any further

위 알고리즘의 각 반복에서는 적어도 하나의 새 함수 종속성이 추가되므로, 종료가 보장된다. 하지만 속성 개수가 n일 때 가능한 종속성은 최대 2n x 2n = 22n개 이므로, 해당 과정은 매우 비효율적일 수 있다.

Closure of Attribute Sets

어떤 속성 B가 α에 의해 함수적으로 결정된다고 할 때, 이는 α→Bα→B가 성립함을 의미한다. 이때 어떤 속성 집합 α가 슈퍼키인지 테스트하려면, α에 의해 함수적으로 결정되는 모든 속성의 집합을 계산하는 알고리즘이 필요하다.