Routing Algorithms: 두 판 사이의 차이
편집 요약 없음 |
편집 요약 없음 |
||
| 24번째 줄: | 24번째 줄: | ||
===Static vs. Dynamic=== | ===Static vs. Dynamic=== | ||
정적 라우팅 알고리즘에서는 패킷의 경로가 시간에 따라 매우 느리게 변화하며, 보통 사람의 개입을 통해서 변경된다.<ref>예를 들면 사람이 직접 링크 비용을 편집하는 방식이다.</ref> 반면 동적 라우팅 알고리즘은 네트워크 트래픽 부하나 topology가 변할 때 라우팅 경로를 변경한다. 동적 알고리즘은 주기적으로 실행되거나 해당 변화에 직접적으로 반응하여 구현된다. 동적 알고리즘은 네트워크 변화에 더 잘 반응할 수 있지만, 라우팅 루프(routing loop)나 경로 진동(route oscillation) 같은 문제에 더 취약할 수 있다. | 정적 라우팅 알고리즘에서는 패킷의 경로가 시간에 따라 매우 느리게 변화하며, 보통 사람의 개입을 통해서 변경된다.<ref>예를 들면 사람이 직접 링크 비용을 편집하는 방식이다.</ref> 반면 동적 라우팅 알고리즘은 네트워크 트래픽 부하나 topology가 변할 때 라우팅 경로를 변경한다. 동적 알고리즘은 주기적으로 실행되거나 해당 변화에 직접적으로 반응하여 구현된다. 동적 알고리즘은 네트워크 변화에 더 잘 반응할 수 있지만, 라우팅 루프(routing loop)나 경로 진동(route oscillation) 같은 문제에 더 취약할 수 있다. | ||
==LS routing algorithm== | |||
LS 라우팅 알고리즘 중 가장 일반적인 알고리즘은 Dijkstra 알고리즘이다. 다익스트라 알고리즘은 네트워크 topology와 모든 링크 비용을 바탕으로 출발 노드(u)에서 다른 모든 노드들까지의 최소 비용 경로를 계산한다. 이때 각 노드는 자신과 연결된 링크들의 식별자와 비용을 담은 링크 상태 패킷(link-state packet)을 네트워크 내의 모든 다른 노드들에게 브로드캐스트(LS broadcast)하여 이를 구현할 수 있다. 다익스트라 알고리즘은 반복적이며, 알고리즘의 '''k번째 반복이 끝난 후에는, 목적지 노드 k개에 대한 최소 비용 경로가 계산된다는 특징'''이 있다. 이때 다익스트라 알고리즘을 설명하기 위한 표기는 다음과 같다: | |||
D(v): 알고리즘의 현재 단계에서 출발 노드에서 목적지 노드 v까지의 최소 비용 경로의 비용 | |||
p(v): 출발 노드에서 목적지 노드 v까지의 현재 단계의 최소 비용 경로에서 v 직전 노드<ref>만약 u → a → b → v와 같이 주어졌다면, p(v)는 b이다.</ref> | |||
N': 최소 비용 경로가 확정된 노드들의 부분집합이다. 즉, v <math>\in</math> N'는 출발 노드에서 v까지의 최소 비용 경로가 확정되었음을 의미한다. | |||
다익스트라 알고리즘은 다음과 같다. | |||
<syntaxhighlight lang="go">Initialization: | |||
N' = {u} | |||
//출발 노드 u와 인접한 노드들에서의 경로 비용을 계산한다. | |||
for all nodes v | |||
if v is a neighbor of u | |||
then D(v) = c(u,v) | |||
else D(v) = ∞ | |||
Loop | |||
find w not in N' such that D(w) is a minimum | |||
add w to N' | |||
//N'에 포함되지 않은 모든 노드들에 대해서 D(v)를 계산한다. | |||
update D(v) for each neighbor v of w and not in N': | |||
//노드 v에 대한 새로 계산된 비용은 이전 단계에서의 비용, 혹은 u ~ w의 경로 비용에 c(w,v)를 더한 값이다. | |||
D(v) = min(D(v), D(w) + c(w,v)) | |||
until N' = N</syntaxhighlight> | |||
다익스트라 알고리즘은 초기화 단계와 반복 루프로 구성되며, 해당 알고리즘은 네트워크에 있는 노드 수 만큼 반복된다. 알고리즘이 종료되면 출발 노드 u에서 네트워크 내의 다른 모든 노드들까지의 최단 경로가 계산된다. Figure 2를 기준으로 최단 경로를 계산하면, 그 결과는 아래 표와 같다. | |||
[[파일:Dijkstra’s algorithm Example.png|대체글=Figure 2. Dijkstra’s algorithm Example|섬네일|Figure 2. Dijkstra’s algorithm Example]] | |||
{| class="wikitable" | |||
|+ | |||
!Step | |||
!N' | |||
!D(v), p(v) | |||
!D(w), p(w) | |||
!D(x), p(x) | |||
!D(y), p(y) | |||
!D(z), p(z) | |||
|- | |||
|0 | |||
|u | |||
|2, u | |||
|5, u | |||
|'''<u>1, u</u>''' | |||
|∞ | |||
|∞ | |||
|- | |||
|1 | |||
|ux | |||
|2, u | |||
|4, x | |||
| | |||
|'''<u>2, x</u>''' | |||
|∞ | |||
|- | |||
|2 | |||
|uxy | |||
|'''<u>2, u</u>''' | |||
|3, y | |||
| | |||
| | |||
|4, y | |||
|- | |||
|3 | |||
|uxyv | |||
| | |||
|'''<u>3, y</u>''' | |||
| | |||
| | |||
|4, y | |||
|- | |||
|4 | |||
|uxyvw | |||
| | |||
| | |||
| | |||
| | |||
|'''<u>4, y</u>''' | |||
|- | |||
|5 | |||
|uxyvwz | |||
| | |||
| | |||
| | |||
| | |||
| | |||
|} | |||
==각주== | ==각주== | ||
[[분류:컴퓨터 네트워크]] | [[분류:컴퓨터 네트워크]] | ||
2025년 4월 30일 (수) 12:31 판
상위 문서: Network Layer
개요
라우팅 알고리즘(Routing algorithm)이란 송신 호스트에서 수신 호스트까지의 "좋은(good)" 경로(path)[1]들을 결정하는 알고리즘을 의미한다. 경로란 패킷이 출발지 호스트에서 목적지 호스트까지 이동할 때 거치는 라우터들의 순서를 의미한다. 이때 "좋은" 경로의 기준은 가장 비용이 적거나(least "cost"), 가장 빠르거나("fastest"), 가장 혼잡하지 않은("least congested") 경로를 의미한다.
Network graph notation

이때 라우팅 알고리즘은 figure 1과 같이 그래프를 사용하여 형식화된다. 그래프 G = (N, E)는 노드들의 집합 N과 간선(edge)들의 모음 E로 구성되며, 각 간선은 N에 속한 두 노드의 쌍이다. 이는 아래와 같이 나타내어 진다.
N = set of routers = {u, v, w, x, y, z}
E = set of links ={(u,v), (u,x), (v,x), (v,w), (x,w), (x,y), (w,y), (w,z), (y,z)}
이때 그래프의 각 노드는 라우터를 의미하며, 간선은 해당 라우터들 간의 물리적인 링크(link)를 의미한다. 간선은 해당 링크의 비용을 나타내는 값을 가진다. 일반적으로 간선의 비용은 해당 링크의 물리적인 길이와 링크의 혼잡도 등에 의해 결정된다. 이때 각 간선과 경로의 비용은 다음과 같이 표기한다.
(x, y) E, c(x,y) = cost of link (x,y) (x, y) E, c(x,y) = //해당 간선은 존재하지 않음 cost of path (x2, x2, x3, ⋯, xp) = c(x1,x2) + c(x2,x3) + ⋯ + c(xp-1,xp)
Routing algorithm classification
라우팅 알고리즘을 분류하는 한가지 방식은 중앙 집중형 라우팅 알고리즘(centralized routing algorithm)과 분산형 라우팅 알고리즘(decentralized routing algorithm)으로 구분하는 것이다. 라우팅 알고리즘을 분류하는 두 번째 방식은 그것이 정적(static)이냐 동적(dynamic)이냐에 따른 것이다.
Centralized vs. Decentralized
중앙 집중형 라우팅 알고리즘은 네트워크에 대한 전체적이고 전역적인 정보(topology[2])를 이용하여 출발지와 목적지 간의 최소 비용 경로를 계산한다. 따라서 해당 알고리즘은 모든 노드 간의 연결 정보와 각각의 링크의 비용을 필요로 한다. 해당 알고리즘은 흔히 LS(link-state) 알고리즘이라고 불린다.
분산형 라우팅 알고리즘은 각각의 라우터 들에 의해서 반복적이고 분산된 방식으로 수행된다. 이때 어떠한 노드도 전체 네트워크의 LS에 대한 완전한 정보를 가지고 있지 않다. 대신 각 노드는 자신에게 직접 연결된 링크들의 비용만 알고 있으므로, 각 노드는 이웃 노드들과의 정보 교환과 계산을 반복하여 최소 비용 경로를 점진적으로 계산한다. 해당 알고리즘은 흔히 DV(distance-vector) 알고리즘이라고 불린다. 왜냐하면 각 노드는 네트워크 내의 다른 모든 노드에 대한 비용의 추정치를 벡터 형태로 유지하기 때문이다.
Static vs. Dynamic
정적 라우팅 알고리즘에서는 패킷의 경로가 시간에 따라 매우 느리게 변화하며, 보통 사람의 개입을 통해서 변경된다.[3] 반면 동적 라우팅 알고리즘은 네트워크 트래픽 부하나 topology가 변할 때 라우팅 경로를 변경한다. 동적 알고리즘은 주기적으로 실행되거나 해당 변화에 직접적으로 반응하여 구현된다. 동적 알고리즘은 네트워크 변화에 더 잘 반응할 수 있지만, 라우팅 루프(routing loop)나 경로 진동(route oscillation) 같은 문제에 더 취약할 수 있다.
LS routing algorithm
LS 라우팅 알고리즘 중 가장 일반적인 알고리즘은 Dijkstra 알고리즘이다. 다익스트라 알고리즘은 네트워크 topology와 모든 링크 비용을 바탕으로 출발 노드(u)에서 다른 모든 노드들까지의 최소 비용 경로를 계산한다. 이때 각 노드는 자신과 연결된 링크들의 식별자와 비용을 담은 링크 상태 패킷(link-state packet)을 네트워크 내의 모든 다른 노드들에게 브로드캐스트(LS broadcast)하여 이를 구현할 수 있다. 다익스트라 알고리즘은 반복적이며, 알고리즘의 k번째 반복이 끝난 후에는, 목적지 노드 k개에 대한 최소 비용 경로가 계산된다는 특징이 있다. 이때 다익스트라 알고리즘을 설명하기 위한 표기는 다음과 같다:
D(v): 알고리즘의 현재 단계에서 출발 노드에서 목적지 노드 v까지의 최소 비용 경로의 비용 p(v): 출발 노드에서 목적지 노드 v까지의 현재 단계의 최소 비용 경로에서 v 직전 노드[4] N': 최소 비용 경로가 확정된 노드들의 부분집합이다. 즉, v N'는 출발 노드에서 v까지의 최소 비용 경로가 확정되었음을 의미한다.
다익스트라 알고리즘은 다음과 같다.
Initialization:
N' = {u}
//출발 노드 u와 인접한 노드들에서의 경로 비용을 계산한다.
for all nodes v
if v is a neighbor of u
then D(v) = c(u,v)
else D(v) = ∞
Loop
find w not in N' such that D(w) is a minimum
add w to N'
//N'에 포함되지 않은 모든 노드들에 대해서 D(v)를 계산한다.
update D(v) for each neighbor v of w and not in N':
//노드 v에 대한 새로 계산된 비용은 이전 단계에서의 비용, 혹은 u ~ w의 경로 비용에 c(w,v)를 더한 값이다.
D(v) = min(D(v), D(w) + c(w,v))
until N' = N
다익스트라 알고리즘은 초기화 단계와 반복 루프로 구성되며, 해당 알고리즘은 네트워크에 있는 노드 수 만큼 반복된다. 알고리즘이 종료되면 출발 노드 u에서 네트워크 내의 다른 모든 노드들까지의 최단 경로가 계산된다. Figure 2를 기준으로 최단 경로를 계산하면, 그 결과는 아래 표와 같다.
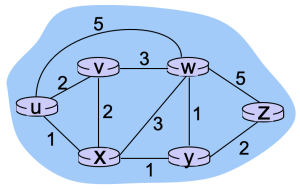
| Step | N' | D(v), p(v) | D(w), p(w) | D(x), p(x) | D(y), p(y) | D(z), p(z) |
|---|---|---|---|---|---|---|
| 0 | u | 2, u | 5, u | 1, u | ∞ | ∞ |
| 1 | ux | 2, u | 4, x | 2, x | ∞ | |
| 2 | uxy | 2, u | 3, y | 4, y | ||
| 3 | uxyv | 3, y | 4, y | |||
| 4 | uxyvw | 4, y | ||||
| 5 | uxyvwz |