Data Structures: 두 판 사이의 차이

2025년 10월 17일 (금) 05:45 판

개요

해당 문서에서는 알고리즘을 구현하기 위해서 사용되는 기초적인 자료구조들에 대해 살펴본다.

Contiguous vs. Linked Data Structures

자료구조는 그것들이 배열에 기반하는지 포인터에 기반하는지에 따라, 연속(contiguous) 또는 연결(linked) 자료구조로 분류될 수 있다. 연속적으로 할당된 자료 구조는 어떤 단일 메모리 덩어리로 구성되며, 배열(arrays), 행렬(matrices), 힙(heaps), 해시 테이블(hash tables)을 포함한다. 연결 자료구조는 포인터로 서로 묶인 여러 메모리 조각들로 구성되며, 리스트(lists), 트리(trees), 그래프 인접 리스트(graph adjacency lists)를 포함한다.

Arrays

배열은 연속 자료구조의 대표 주자이다. 배열은 고정된 크기의 데이터 레코드들로 이루어진 자료 구조이며, 각 원소는 해당 인덱스나 주소를 통해서 효율적으로 탐색될 수 있다. 배열의 장점은 아래와 같다:

인덱스가 주어졌을 때 해당 원소에 상수 시간에 접근할 수 있다.
공간 효율성: 배열은 순수하게 저장하는 데이터로만 이루어져 있으므로 포인터나 기타 서식 정보로 메모리가 낭비되지 않는다.
메모리 지역성(locality): 많은 프로그래밍 작업은 자료구조의 모든 원소를 순회(iterate)하는데, 이때 메모리 지역성이 높다면 캐시(Cache)가 더욱 활용되어 프로그램의 속도가 빨라진다.

하지만 배열의 단점은 프로그램의 실행 도중 그 크기를 조절할 수 없다는 것이다. 만약 우리가 n개의 레코드만을 위한 공간을 할당했는데 (n+1)번째 고객을 추가하려 하면 프로그램은 곧바로 실패한다. 매우 큰 배열을 잡아두는 것으로 보완할 수 있으나, 이는 공간을 낭비하여 다시금 프로그램이 할 수 있는 일을 제한한다.

Dynamic Arrays

사실 이러한 단점은 동적 배열(dynamic array)를 통해서 일정 부분 해결할 수 있다. 크기를 1의 배열로 시작하여 공간이 모자랄 때마다 크기를 m에서 2m으로 두 배로 만드는 방식으로 동적 배열을 구현한다고 가정하자. 이는 크기 2m의 새로운 연속 배열을 할당하고, 기존 배열의 내용을 새 배열의 첫 절반 부분에 복사한 후, 기존 배열이 점유한 메모리를 반환하여 이루어진다. 해당 과정에서 실제로 수행되는 작업의 양을 구하는 과정은 아래와 같다:

1. 배열이 n개의 항목을 저장할 메모리를 할당 받기까지는  $⌈ l o g_{2} (n) ⌉$ 번의 메모리 복사가 필요하다. 
2.  $n = 2^{j}$ 인 어떤 j에서 마지막으로 삽입하면 한 번더 복사해야 한다.(n이 최악의 경우)
3. 1, 2에 따르면 복사 작업은 첫 번째/두 번째/네 번째.../n번째 삽입 후에 일어난다. 
4. 이때 i 번째 삽입에서 메모리 복사 작업을 진행할 때, 총 메모리 복사 횟수는  $2^{i - 1}$ 이므로, 총 복사 횟수는:
 $M = n + \sum_{i = 1}^{l o g_{2} (n)} 2^{i - 1} = 1 + 2 + 4 + 8 + \dots + n + n = \sum_{i = 0}^{l o g_{2} (n)} \frac{n}{2^{i}} \leq n \sum_{i = 0}^{\infty} \frac{1}{2^{i}} = 2 n$

따라서 n개의 각 원소는 배열에 차례되로 삽입될 때 평균적으로 단 두번만 접근된다. 따라서 동적 배열을 관리하는 총 작업량은 처음부터 충분히 큰 단일 배열을 미리 할당했을 때와 마찬가지로 O(n)이다. 동적 배열을 사용할 때의 단점은 각 삽입이 상수 시간에 이루어진다는 보장을 받지 못한다는 것이다. 모든 인덱스 접근과 대부분의 삽입은 빠르지만, 배열의 복사를 야기하는 소수의 삽입이 존재하기 때문이다. 하지만 그럼에도 n번째 원소 삽입까지 요구되는 시간 복잡도는 O(2n)이라는 점에서 충분히 빠르다고 볼 수 있다.

Sentinels

삽입 정렬과 같은 알고리즘에서, 원소를 왼쪽으로 이동시키며 삽입할 때 검사하는 인덱스에 대한 경계 조건을 체크해야 한다.^[1] 이러한 경계 조건의 체크는 코드를 복잡하게 만든다. 이러한 문제를 해결하기 위해서 감시자 원소(sentinel)를 사용한다. 이는 $\pm \infty$ 와 같이 비교에서 절대 선택되지 않을 값을 택하는 방식으로 구현된다. 예를 들어 삽입 정렬에서 배열의 왼쪽 끝에 $- \infty$ 와 같이 가짜 원소를 두어 경계 조건을 체크할 필요성을 없애는 것이다. 이는 코드를 더욱 깔끔하게 만들 수 있으며, 성능에도 영향을 주지 않아 권장되는 구현 방식 중 하나이다.

Pointers and Linked Structures

연결 자료구조(linked structure)는 기본적으로 아래와 같은 구조를 지닌다:

typedef struct list {
    item_type item;      /* data item */
    struct list *next;   /* point to successor */
} list;

위에서 연결 자료구조(list)의 각 노드는 데이터를 저장하는 하나 이상의 필드(item)를 포함한다. 또한 각 노드는 적어도 하나의 다른 노드(*next)에 대한 포인터 필드(next)를 포함한다. 마지막으로 연결 자료구조의 시작 노드(head)를 가리키는 포인터가 필요하다. 이러한 구조는 보통 연결 리스트(linked list)라고도 불리며, 가장 단순한 연결 자료구조에 속한다. 리스트가 지원하는 세 가지 기본 연산은 탐색, 삽입, 삭제이다.

Searching a List

연결 리스트에서 항목 x를 탐색하는 것은 반복적으로(iterative) 또는 재귀적으로(recursive) 할 수 있다. 본 문서에서는 재귀적인 탐색 방식을 다룬다. 이는 아래와 같이 구현된다.

list *search_list(list *l, item_type x) { // l은 현재 탐색할 노드를 가리킴
    if (l == NULL) {
        return(NULL);
    }
    if (l->item == x) {
        return(l);
    } else {
        return(search_list(l->next, x));
    }
}

Insertion into a List

리스트를 어떤 특정한 순서로 유지할 필요는 없기 때문에, 편리한 위치에 항목을 새로 삽입하면 된다. 이는 아래와 같이 구현된다.

void insert_list(list **l, item_type x) { //l은 리스트의 head 노드에 대한 포인터
    list *p; /* temporary pointer */
    p = malloc(sizeof(list));
    p->item = x;
    p->next = *l; // *l은 연결 리스트의 head 노드
    *l = p;
}

Deletion From a List

연결 리스트에서 특정 노드를 삭제하는 것은 다소 복잡하다. 이를 구현하기 위해서는 먼저 삭제하고자 하는 노드를 가리키는 포인터를 찾아야 한다. 이는 아래와 같이 구현된다:

list *item_ahead(list *l, list *x) { //l은 현재 탐색할 노드, x는 삭제하고자 하는 노드의 주소
    if ((l == NULL) || (l->next == NULL)) { //결국 찾지 못한 경우(x == head 노드의 주소인 경우 포함)
        return(NULL);
    }
    if ((l->next) == x) { // 찾고자 하는 노드를 찾았음
        return(l);
    } else {              // 해당 노드는 찾고자 하는 노드가 아님
        return(item_ahead(l->next, x));
    }
}

*item_ahead() 함수는 삭제하고자하는 노드의 선행 노드(혹은 head)를 반환한다. 따라서 해당 선행 노드의 next 포인터(혹은 head 자체)를 변경해야 한다. 이는 아래와 같이 구현된다.

void delete_list(list **l, list **x) { // l은 head 노드에 대한 포인터, x는 삭제할 노드에 대한 포인터
    list *p;    /* item pointer */
    list *pred; /* predecessor pointer */
    p = *l;
    pred = item_ahead(*l, *x); // 삭제할 노드의 선행 노드 탐색
    if (pred == NULL) {        // 해당 경우는 x가 연결 리스트의 해당 노드이므로 x의 선행 노드가 존재하지 않음
        *l = p->next;
    } else {                   // 일반적인 경우
        pred->next = (*x)->next;
    }
    free(*x);   /* free memory used by node */
}

Singly or Doubly Linked Lists

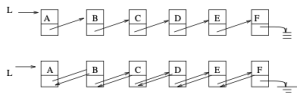
단일 연결 리스트(Singly Linked List)는 위에서 살펴본 것과 같이 각 노드가 다음 노드에 대한 포인터만 가지고 있다. 따라서 앞에서부터 단방향으로 순회한다. 이는 메모리 사용량이 적다는 장점이 있지만, 특정 노드의 이전 노드를 찾기 위해서는 항상 head부터 순회해야 한다는 단점이 있다.

이중 연결 리스트(Doubly Linked List)는 단일 연결 리스트와 달리 각 노드가 next와 prev 두개의 포인터를 가지고 있어 리스트를 양방향으로 탐색할 수 있도록 하는 자료구조 있다. 따라서 특정 노드 x가 주어졌을 때 해당 노드의 선행 노드를 찾는 작업의 시간 복잡도가 O(1)로 줄어든다는 장점이 있다. 또한 양방향 순회가 가능하다는 장점이 있다. 하지만 포인터를 하나 더 저장해야 하므로 메모리 사용량이 증가한다는 단점이 있다.

탐색, 삽입, 삭제 같은 기본 연산의 시간 복잡도는 단일 연결 리스트와 이중 연결 리스트가 동일하다. 즉, 이중 연결 리스트가 더 많은 포인터를 쓰긴 하지만 추가적인 Big-O 비용은 없다. 따라서 해당 위키에서는 많은 경우 이중 연결 리스트로 설정할 것이다.

Advantages of Linked Lists

연결 구조(리스트)의 장점은 아래와 같다:

메모리가 실제로 가득 차지 않는 이상, 오버플로우가 결코 발생하지 않는다.
삽입과 삭제가 배열보다 더욱 단순하다.
저장할 데이터의 크기가 큰 경우, 항목 자체를 옮기는 것 보다 포인터를 옮기는 것이 더욱 쉽고 빠르다.

Containers: Stacks and Queues

컨테이너란 그 내용과 무관하게 데이터 항목을 저장하고 검색할 수 있도록 하는 추상자료형을 의미한다. 이를 대표하는 자료형으로 스택(stack)과 큐(queue)가 존재한다. 이들은 모두 원소를 꺼내는 순서가 값과 무관하고 삽입 순서로 결정된다는 공통점을 가진다. 또한 스택과 큐의 기본 연산은 배열/연결 리스트로 구현할 시 O(1) 시간 복잡도로 구현할 수 있다.^[2]

Stacks

스택(Stack)은 LIFO(Last-In, First-Out) 원칙에 따라 검색을 지원하는 자료구조이다. 스택의 삽입과 삭제 연산은 보통 push와 pop이라고 불리며, 아래와 같은 함수 꼴로 설명할 수 있다:

Push(x, s): 항목 x를 스택의 top에 삽입한다.
Pop(s): 스택의 top의 항목을 반환하고 제거한다.

스택은 배열로 간단하게 구현할 수 있다. 이는 메모리 지역성 덕분에 캐시에 친화적이고, 매우 빠르다는 장점이 있다. 스택은 DFS(깊이 우선 탐색)를 구현할 때 주로 사용된다.

Queues

큐(Queue)는 FIFO(First-In, First-Out) 원칙에 따라 검색을 지원하는 자료구조이다. 큐의 삽입과 삭제 연산은 보통 Enqueue와 Dequeue이라고 불리며, 아래와 같은 함수 꼴로 설명할 수 있다:

Enqueue(x, q): 큐의 뒤(back)에 x를 넣는다.
Dequeue(q): 큐의 앞(front) 원소를 반환하며 제거한다.

큐는 연결 리스트로 간단하게 만들 수 있다. 이는 자료구조에 대한 크기 제약이 거의 존재하지 않는다는 장점이 있다. 만약 지역성을 위해서 배열로 구현하고자 한다면, 인덱스 front, rear를 모듈러 연산을 통해 순환시키는 방식으로 원형 버퍼를 만들어야 한다. 큐는 BFS(너비 우선 탐색)를 구현할 때 주로 사용된다.

Dictionary

딕셔너리(Dictionary) 자료형은 저장된 데이터(key, 키)를 통해서 데이터 항목에 접근할 수 있게 한다. 딕셔너리가 지원하는 기본 연산은 아래와 같다:

Search(D, k): 검색 키 k가 주어졌을 때, 딕셔너리 D 안에서 키 값이 k인 원소의 포인터를 반환한다.
Insert(D, x): 데이터 항목 x가 주어졌을 때, 이를 딕셔너리 D에 추가한다.
Delete(D, x): 딕셔너리 D 안의 특정 데이터 항목에 대한 포인터 x가 주어졌을 때, 이를 D에서 제거한다.
Max(D)/Min(D): D에서 가장 큰/작은 키 값을 가진 항목을 가져온다.
Logical Predecessor(D, x)/Successor(D, x): 항목 x를 완전 정렬 시킨 순열 S를 기준으로 항목 x의 바로 이전(다음) 키 값을 가진 항목을 D에서 가져온다.

중요한 것은 이들 연산들에 대해 동시에 최적의 시간 복잡도를 가지는 자료 구조는 없다는 것이다. 아래는 배열을 기반으로 사전을 구현했을 때, 정렬 여부에 따른 각 연산의 시간 복잡도를 나타낸 표이다.


연산	Unsorted Arrays	Sorted Arrays
Search(S, k)	O(n)	O(log n)^[3]
Insert(S, x)	O(1)	O(n)
Delete(S, x)	O(1)	O(n)
Min(S), Max(S)	O(n)	O(1)
Predecessor, Successor	O(n)	O(1)

즉, 상황에 따라 적절한 자료구조를 선택해야 한다.

Binary Search Tree

자세한 내용은 Binary Search Tree 문서를 참조해주십시오.

Hash Table

자세한 내용은 Hash Table 문서를 참조해 주십시오.

Priority Queues

자세한 내용은 Priority Queues 문서를 참조해 주십시오.

Union-Find

Union-Find 자료구조는 두 연산(Find, Union)을 효율적으로 수행하기 위해 사용하는 자료구조이다. Kruskal 알고리즘의 경우와 같이 그래프의 여러 정점들을 여러 집합으로 관리할 때, 두 정점이 같은 연결요소(component)에 속하는지, 또는 두 집합을 합칠지를 빠르게 판단해야 한다. 이때 사용하는 연산은:

Find(i): i가 속한 “집합의 대표(root)”를 반환.
- 부모 포인터(parent[i])를 따라 루트까지 올라가면서 찾는다.
- 즉, while (parent[i] != i) → 위로 계속 이동.
Union(i, j): 원소 i와 j가 속한 집합을 하나로 합친다.
- 두 집합의 루트를 찾아, 한쪽 루트를 다른 루트 밑에 붙인다.
- 즉, “find(i) == find(j)”가 되도록 만든다.

이를 구현하기 위해서 각 집합(set)은 하나의 트리로 표현된다. 이때 각 트리의 루트 노드(root)가 해당 집합의 “대표 이름(name of the set)”에 해당한다. 또한 각 노드는 “부모 포인터(parent pointer)”를 가지므로, 각 원소는 자신의 부모를 알고 있고, 루트는 자기 자신을 부모로 가진다. Figure 1은 이를 잘 보여준다. 왼쪽의 각 트리 자료구조는 각각의 집합을 나타내며, 오른쪽 그림은 각 원소의 부모는 나타내는 배열 p[i]를 보여준다.

Implementation of Union-Find

Union-Find 자료구조는 아래와 같이 구현된다:

typedef struct {
    int p[SET_SIZE+1];   // 각 노드의 부모 (parent)
    int size[SET_SIZE+1]; // 각 트리(집합)의 크기
    int n;                // 전체 원소 개수
} union_find;

void union_find_init(union_find *s, int n) {
    for (i = 1; i <= n; i++) {
        s->p[i] = i;     // 자기 자신이 루트
        s->size[i] = 1;  // 트리 크기는 1
    }
    s->n = n;
}

즉, 시작할 때는 각 원소가 자기 자신만 포함하는 독립 집합 상태이다.

Union by Size

단순한 Union-Find에서는 Union(i, i+1)을 순서대로 하면 트리가 한 줄로 쭉 이어지는 형태가 된다. 이 경우 Find(1)을 하면 루트까지 O(n)의 시간복잡도가 소요된다. 따라서 Union 연산울 실행할 때, 트리의 “높이(height)”가 커지는 걸 방지해야 한다. 이를 방지하기 위해서는 작은 트리(subtree)를 큰 트리 밑으로 붙이는 방법을 사용해야 한다. 즉, 즉, 노드 수가 더 적은 쪽이 자식이 되고, 더 많은 쪽이 부모(root)가 된다. 이 기법을 Union by Size(Union by Rank)라고 한다.

이 방식으로 사용하면 트리 높이가 매번 1씩 증가하지 않고, 로그(log) 수준으로만 증가한다. 따라서 전체 Union-Find 구조의 Find/Union 연산은 거의 O(log n) 이하로 작동한다.

Path Compression

Path Compression은 Union by Size 방식보다 더욱 빠른 영상을 가능케 하는 방식이다. 이상적인 Union-Find 트리 구조는 깊이가 1인 트리이다. 이런 트리 구조에서는 Find 연산의 시간복잡도는 O(1)이기 때문이다. 따라서 Path Compression 방식은 Find 연산 중의 과정에서 만난 모든 노드들이 바로 루트를 가리키게 수정하도록 하는 것을 핵심적인 아이디어로 삼는다. Figure 2는 왼쪽 트리가 주어졌을 때, Find(4)를 수행하면 4 → 3 → 2 → 1을 따라 루트를 찾는 과정에서 만난 모든 노드(4, 3, 2)의 부모 포인터를 1로 직접 갱신하는 것을 보여준다. 이를 통해서 트리의 높이를 확 줄일 수 있다.

이 경우 Union-Find 연산들의 평균 수행 시간이 O(α(n))로 감소한다. 이때 α(n)은 inverse Ackermann function(역 아커만 함수)인데, n이 우주에 존재하는 원자 수보다 커도 α(n) <= 5입니다. 따라서 아무리 큰 그래프라도 “상수 시간”에 가깝게 동작한다.

각주

↑ j >= 0과 같은 조건을 의미한다. 즉, 빈 배열인지? 인덱스가 음수가 아닌지? 등을 확인하기 위한 것이다.
↑ 스택의 경우에는 push/pop/top/isEmpty, 큐의 경우에는 enqueue/dequeue/front/isEmpty 연산이 해당한다.
↑ 이진 탐색을 사용할 수 있기 때문이다.

[1] >= 0과 같은 조건을 의미한다. 즉, 빈 배열인지? 인덱스가 음수가 아닌지? 등을 확인하기 위한 것이다.

[2] 스택의 경우에는 push/pop/top/isEmpty, 큐의 경우에는 enqueue/dequeue/front/isEmpty 연산이 해당한다.

[3] 이진 탐색을 사용할 수 있기 때문이다.

[1]

[2]

[3]

익명 사용자

검색

Data Structures: 두 판 사이의 차이

이름공간

더 보기

문서 행위

2025년 10월 17일 (금) 05:45 판

목차

개요

Contiguous vs. Linked Data Structures

Arrays

Dynamic Arrays

Sentinels

Pointers and Linked Structures

Searching a List

Insertion into a List

Deletion From a List

Singly or Doubly Linked Lists

Advantages of Linked Lists

Containers: Stacks and Queues

Stacks

Queues

Dictionary

Binary Search Tree

Hash Table

Priority Queues

Union-Find

Implementation of Union-Find

Union by Size

Path Compression

각주

둘러보기

둘러보기

위키 도구

위키 도구

@@ 203번째 줄: / 203번째 줄: @@
 ===Path Compression===
-Path Compression은 Union by Size 방식보다 더욱 빠른 영상을 가능케 하는 방식이다. 이상적인 Union-Find 트리 구조는 깊이가 1인 트리이다. 이런 트리 구조에서는 Find 연산의 시간복잡도는 O(1)이기 때문이다. 따라서 Path Compression 방식은 Find 연산 중의 과정에서 만난 모든 노드들이 바로 루트를 가리키게 수정하도록 하는 것을 핵심적인 아이디어로 삼는다. Figure
+Path Compression은 Union by Size 방식보다 더욱 빠른 영상을 가능케 하는 방식이다. 이상적인 Union-Find 트리 구조는 깊이가 1인 트리이다. 이런 트리 구조에서는 Find 연산의 시간복잡도는 O(1)이기 때문이다. 따라서 Path Compression 방식은 Find 연산 중의 과정에서 만난 모든 노드들이 바로 루트를 가리키게 수정하도록 하는 것을 핵심적인 아이디어로 삼는다. Figure 2는 왼쪽 트리가 주어졌을 때, Find(4)를 수행하면 4 → 3 → 2 → 1을 따라 루트를 찾는 과정에서 만난 모든 노드(4, 3, 2)의 부모 포인터를 1로 직접 갱신하는 것을 보여준다. 이를 통해서 트리의 높이를 확 줄일 수 있다.
+이 경우 Union-Find 연산들의 평균 수행 시간이 O(α(n))로 감소한다. 이때 α(n)은 inverse Ackermann function(역 아커만 함수)인데, n이 우주에 존재하는 원자 수보다 커도 α(n) <= 5입니다. 따라서 아무리 큰 그래프라도 “상수 시간”에 가깝게 동작한다.
 <syntaxhighlight lang="c">

익명 사용자

검색

Data Structures: 두 판 사이의 차이

2025년 10월 17일 (금) 05:45 판

개요

Contiguous vs. Linked Data Structures

Arrays

Dynamic Arrays

Sentinels

Pointers and Linked Structures

Searching a List

Insertion into a List

Deletion From a List

Singly or Doubly Linked Lists

Advantages of Linked Lists

Containers: Stacks and Queues

Stacks

Queues

Dictionary

Binary Search Tree

Hash Table

Priority Queues

Union-Find

Implementation of Union-Find

Union by Size

Path Compression

각주

둘러보기

위키 도구

문서 도구

분류 목록