The Big Oh Notation: 두 판 사이의 차이
편집 요약 없음 |
편집 요약 없음 |
||
| 1번째 줄: | 1번째 줄: | ||
[[분류:알고리즘 설계와 분석]] | [[분류:알고리즘 설계와 분석]] | ||
[[분류:컴퓨터 공학]] | [[분류:컴퓨터 공학]] | ||
상위 문서: [[알고리즘 설계와 분석#알고리즘 분석|알고리즘 설계와 분석]] | |||
==개요== | ==개요== | ||
2025년 9월 5일 (금) 22:49 판
상위 문서: 알고리즘 설계와 분석
개요
주어진 어떤 알고리즘에 대한 시간 복잡도는 가능한 문제 인스턴스 크기에 대한 함수들이며, 이들을 정밀하게 다루는 것은 매우 어렵다. 따라서 이들을 단순화하여 분석하는 것이 매우 좋은 방식 중 하나이다. 예를 들어, 와 같은 시간 복잡도 함수는 정밀하게 분석하기란 매우 어렵지만, 시간 복잡도가 n에 대해 2차적으로 증가한다는 관찰이 틀렸다고 볼 수는 없다.
해당 문서에서는 이러한 특성을 이용한 “빅 오(Big Oh)” 표기에 대해 알아본다.
내용
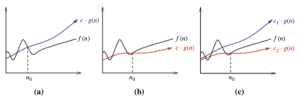
“빅 오(Big Oh)” 표기는 시간 복잡도 함수를 상한/하한으로 나타내어 이를 단순화 하는 방식이다. 함수 과 은 빅 오 분석에서 동일하다. 빅 오 표기에는 아래와 같은 세 가지 정의가 존재한다.
- 는 가 에 대한 상한임을 의미한다.
- 따라서 어떤 상수 c가 존재하여 충분히 큰 모든 n에 대하여 가 성립한다.
- 는 가 에 대한 하한임을 의미한다.
- 따라서 어떤 상수 c가 존재하여 충분히 큰 모든 n에 대하여 가 성립한다.
- 는 가 에 대한 상한이고 가 에 대한 하한임을 의미한다.
- 따라서 어떤 상수 c1, c2가 존재하여 충분히 큰 모든 n에 대하여 가 성립한다.
이러한 정의들은 figure 1에 잘 제시되어 있다. 이들 정의 각각은 어떤 상수 n0가 존재하여 그 이후에는 조건이 만족된다는 것을 보여준다.
Working with the Big Oh
일반적인 대수 계산을 빅 오 표기에 적용하는 것은 중요하면서도 조금 모호하다. 이는 대부분의 대수 계산에 대한 상식이 유지되면서도 꼭 모두 적용된다고는 말할 수 없기 때문이다.
Big Oh Addition/Subtraction
어떠한 차수가 같은 함수 에 대해 를 가정해 보자. 이때 함수 에 대한 빅 오 표기는 아래와 같이 계산할 수 있다.
이라 하면
즉, 같은 차수의 함수끼리 더해도 결국 그 차수는 변하지 않는다. 하지만 빅 오 표기에서의 뺄셈은 최대 차수의 계수에 따라 그 결과가 달라지기 때문에, 모호하게 작동한다. 예를 들어 함수 에 대해:
이라면 , 이라면,
따라서 어떤 차수가 같은 함수 에 대해 뺼셈을 진행한다면, 일반적으로 라고 말할 수 있을 뿐이며, 해당 차수가 보존되는 지에 대해서는 말할 수 없다.
Multiplying Functions
곱셈은 반복된 덧셈과 같이 취급할 수 있다. 따라서, 를 만족하는 상수 c에 대해 아래와 같이 계산된다.
하지만 증가함수인 두 함수를 서로 곱하는 경우에는, 두 함수가 모두 결과에 준다. 이는 아래와 같이 나타낼 수 있다.
Reasoning about Efficiency
알고리즘의 실행 시간에 대한 추론은 보통 쉽다. 이에 대한 예시는 Sorting Problem에 대한 문서를 참조하면 된다.