컴퓨터에서의 수 표현: 두 판 사이의 차이
편집 요약 없음 |
|||
| 46번째 줄: | 46번째 줄: | ||
* U2S(x) = x - 2<sup>w</sup> <math>\times</math> MSB(x) | * U2S(x) = x - 2<sup>w</sup> <math>\times</math> MSB(x) | ||
또한 C에서의 형변환은 implicitly하게 발생하기도 한다. 예를 들어서 signed 정수와 unsigned 정수가 한 수식 내에서 혼용되어 사용된다면, signed 정수는 unsigned 정수로 암묵적으로 형변환된다.<ref>기본적으로 10과 같은 정수 문자열은 signed로 해석된다. 이를 unsigned로 표현하고자 할 때는 10U와 같이 말미에 'U'를 사용하여야 한다.</ref> | 또한 C에서의 형변환은 implicitly하게 발생하기도 한다. 예를 들어서 signed 정수와 unsigned 정수가 한 수식 내에서 혼용되어 사용된다면, signed 정수는 unsigned 정수로 암묵적으로 형변환된다.<ref>기본적으로 10과 같은 정수 문자열은 signed로 해석된다. 이를 unsigned로 표현하고자 할 때는 10U와 같이 말미에 'U'를 사용하여야 한다.</ref> | ||
===정수의 연산=== | |||
[[파일:UnsignedAdd.png|테두리|프레임없음|500x500픽셀]] | |||
unsigned 정수의 덧셈은 bit sequence를 각각의 자릿수에 맞는 bit끼리 더하고 받아올림값이 있다면 이를 적용하며 수행한다.. 이때 carry output이라고 하는 w를 초과하는 자릿수에 해당하는 받아올림값은 무시한다. 이는 결과적으로 modular sum<ref>UAdd<sub>w</sub>(U, V) = (u + v) mod 2<sup>w</sup></ref>에 해당한다. | |||
[[파일:SignedAdd.png|테두리|프레임없음|500x500픽셀]] | |||
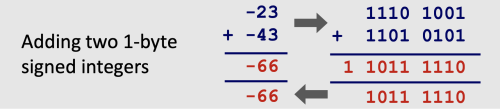
signed 정수의 덧셈 또한 unsigned 정수의 덧셈과 거의 유사한 형태로 수행한다. bit sequence의 연산은 unsigned 정수와 동일한 방식으로 하되, 그 결과의 해석을 2의 보수법으로 하면 되는 것이다. | |||
unsigned 정수의 뺄셈은 x - y를 x + | |||
이때 unsiged와 signed 정수를 더할 때 그 범위를 초과하는 경우를 Overeflow | |||
==각주== | ==각주== | ||
[[분류:컴퓨터 시스템]] | [[분류:컴퓨터 시스템]] | ||
2025년 3월 13일 (목) 00:26 판
개요
본문에서는 컴퓨터가 정수를 표현하는 방식에 대해서만 다룬다.
0보다 작은 정수 표현하기
sign-magnitude
첫번째 bit를 부호를 지정하는sign bit로 사용하는 방식이다.
- sign bit 0: 양수 010101012 = +8510
- sign bit 1: 음수 110101012 = -8510
장점과 단점이 존재한다.
2의 보수법
2의 보수법(Two's Complement)이란 각각의 bit를 다음의 방식으로 해석하는 표현법이다.
이때 2의 보수법을 적용하는 2진수에서의 first bit를 MSB(Most Significant Bit)라고 한다. MSB가 1이면 음수, 0이면 0이상의 정수이다.
아래는 2의 보수법을 적용하여 해석한 2진수이다.
- 0b01010 = 0 + 8 + 2 + 0 = 10
- 0b10110 = -16 + 0 + 4 + 2 + 0 = -10
Unsigned vs Signed
2의 보수법을 적용하여 동일한 2진 벡터를 다른 방식으로 해석할 수 있다. 아래는 그 예시이다.
- unsigned: 0b10110 = 16 + 0 + 4 + 2 + 0 = 22
- 2의 보수법: 0b10110 = -16 + 0 + 4 + 2 + 0 = -10
서로 다른 해석법 때문에 2진 벡터의 길이가 w일 때 unsigned 해석법과 2의 보수법은 각각 다른 범위를 가진다.
- unsigned 범위: 0 ~ 2w-1
- 2의 보수법 범위: -2w-1 ~ 2w-1 - 1
이때 x > 0이라면, 2의 보수법으로 해석된 음의 정수 -x를 unsigned 방식으로 해석하면 2w-x에 대응한다.
- B2Sw(1011) = -5, B2Uw(1011) = 11
Unsigned와 Signed 사이의 변환
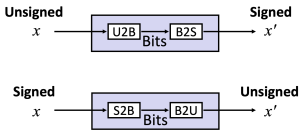
signed 정수와 unsigned 정수사이에서의 변환은 해당 정수의 bit 패턴을 재해석하여 이루어진다. 오른쪽 그림은 컴퓨터 내에서 explicit 타입 변환이 어떤 방식으로 이루어지는지 보여준다. [1] 또한 Unsigned 정수와 Signed 정수 사이의 변환에는 다음과 같은 관계가 성립한다.
- S2U(x) = x + 2w MSB(x)
- U2S(x) = x - 2w MSB(x)
또한 C에서의 형변환은 implicitly하게 발생하기도 한다. 예를 들어서 signed 정수와 unsigned 정수가 한 수식 내에서 혼용되어 사용된다면, signed 정수는 unsigned 정수로 암묵적으로 형변환된다.[2]
정수의 연산
unsigned 정수의 덧셈은 bit sequence를 각각의 자릿수에 맞는 bit끼리 더하고 받아올림값이 있다면 이를 적용하며 수행한다.. 이때 carry output이라고 하는 w를 초과하는 자릿수에 해당하는 받아올림값은 무시한다. 이는 결과적으로 modular sum[3]에 해당한다.
signed 정수의 덧셈 또한 unsigned 정수의 덧셈과 거의 유사한 형태로 수행한다. bit sequence의 연산은 unsigned 정수와 동일한 방식으로 하되, 그 결과의 해석을 2의 보수법으로 하면 되는 것이다.
unsigned 정수의 뺄셈은 x - y를 x +
이때 unsiged와 signed 정수를 더할 때 그 범위를 초과하는 경우를 Overeflow