Pumping Lemma: 두 판 사이의 차이
| 35번째 줄: | 35번째 줄: | ||
Pumping Lemma를 직접 적용하기 전에, 정규언어에 대한 다른 성질(closure property) 을 함께 이용하면 증명이 쉬워진다. 아래와 같은 언어가 비정규 언어라는 것을 증명해보자: | Pumping Lemma를 직접 적용하기 전에, 정규언어에 대한 다른 성질(closure property) 을 함께 이용하면 증명이 쉬워진다. 아래와 같은 언어가 비정규 언어라는 것을 증명해보자: | ||
<math>L=\{w\in \{0,1,2\}*|\#0(w)+\#(1)=\#(2)\}</math> | <math>L=\{w\in \{0,1,2\}*|\#0(w)+\#(1)=\#(2)\}</math> | ||
위 언어는 | 위 언어는 문자열 안의 0과 1의 개수의 합이 2의 개수와 같아야 하는 언어이다. 위 언어가 비정규임을 보이기 위해, L이 정규라고 가정하자. 또한 정규언어는 교집합에 대해 닫혀 있음(closure under intersection)을 이용하면, 아래와 같은 언어 또한 정규 언어이다: | ||
<math>L \cap 0*1*2* = \{0^m1^n2^{m+n}|m\ge0,n\ge0\}</math> | <math>L \cap 0*1*2* = \{0^m1^n2^{m+n}|m\ge0,n\ge0\}</math> | ||
이때 pumping lemma를 위 교집합 언어에 적용해보자: | 이때 pumping lemma를 위 교집합 언어에 적용해보자: | ||
2025년 11월 12일 (수) 23:21 기준 최신판
상위 문서: Regular Languages
개요
DFA는 유한한 개수의 상태(state)만을 가진다. 만약 DFA가 무한한 문자열을 인식하는 언어 L 을 인식한다고 할때, 충분히 긴 문자열을 입력하면, 반드시 같은 상태를 두 번 이상 방문하게 된다. 이때 반복된 부분을 여러 번 반복(pumping)할 수 있고 여전히 DFA가 받아들이므로, DFA가 인식하는 모든 정규언어에는 특정한 반복 구조가 존재한다. 이 논리에서 pumping lemma가 출발하며, 이는 아래와 같다:
L이 정규언어라면, 어떤 펌핑 길이 p가 존재한다. 이때 길이가 p 이상인 모든 문자열은 세 부분 x, y, z로 분해할 수 있으며, 아래 조건을 만족한다. 1. 2. 3.
이를 논리식으로 나타내면 아래와 같다:
먼저, 1번 조건은 y 부분을 0번, 1번, 2번… 아무 번이든 반복해도 여전히 언어 L에 속해야 한다는 것을 의미한다. 예를 들어 일때 , 일때 , 일때 등등이 모두 L에 속해야 한다는 것이다.
또한 2번 조건은 반복 부분 y의 길이는 0이 아니며, 반드시 실제로 반복되는 구간이 존재해야 한다는 뜻이다.
마지막으로 3번째 조건은 반복되는 부분 y는 문자열의 처음 부분 p 이내에 존재해야 한다는 것이다. 즉, 반복(pumping)되는 부분은 문자열의 앞부분에 있다. 이는 DFA가 구조적으로 상태가 p개만 존재하기 때문에, 길이가 p 이상이면 반드시 어떤 상태가 다시 반복되기 때문이다.
Pumping Lemma를 다른 말로 표현하면, 이 정규 언어라면 의 문자열 길이들의 집합은 등차수열을 포함한다는 것이다.
Applying the Pumping Lemma
이는 어떤 언어가 정규언어는 아니라는 것을 보이는 데에 사용된다. 예를 들어, 아래와 같은 언어를 고려하자:
B가 정규 언어라고 가정하면, 아래와 같이 B가 정규 언어가 아님을 보일 수 있다:
- Pumping Lemma에 따라 어떤 길이 p가 존재한다.
- 로 선택한다.(길이가 )
- 이때 B는 정규언어이므로, 조건에 따라 로 분해된다.
- 이때 이므로, y는 반드시 0으로만 구성된다.
- 이때 이므로, pumping lemma에 따라 이때 도 B에 속해야 한다.
- 하지만 0과 1의 개수가 다르므로 는 B에 속하지 않고, 모순이 발생한다.
위와 같은 증명의 결론은 B가 정규언어가 아니라는 것이다.
Using Other Facts with the PL
Pumping Lemma를 직접 적용하기 전에, 정규언어에 대한 다른 성질(closure property) 을 함께 이용하면 증명이 쉬워진다. 아래와 같은 언어가 비정규 언어라는 것을 증명해보자:
위 언어는 문자열 안의 0과 1의 개수의 합이 2의 개수와 같아야 하는 언어이다. 위 언어가 비정규임을 보이기 위해, L이 정규라고 가정하자. 또한 정규언어는 교집합에 대해 닫혀 있음(closure under intersection)을 이용하면, 아래와 같은 언어 또한 정규 언어이다:
이때 pumping lemma를 위 교집합 언어에 적용해보자:
- 펌핑 길이를 p라고 하고, 를 선택한다.
- PL에 따라 이므로 는 오직 0으로만 이루어 져야 한다.()
- 따라서 가 되어야 하는데, 이는 에 속하지 않는다.
Pumping Lemma for CFLs
PL은 CFL(Context-Free Language)에도 적용할 수 있다. 이는 아래와 같다:
만약 L이 CFL이라면, 충분히 긴 문자열 에 대해 를 아래와 같이 5부분으로 나눌 수 있다:
이때 아래의 세 조건이 항상 성립한다:
- : 즉, v와 y 부분을 “반복(pumping)”해도 여전히 L 안에 속한다.
- : v와 y 중 적어도 하나는 비어 있지 않아야 한다.[1]
- : v, x, y의 길이는 일정한 상한 p 이하이다.
위 개념을 구체화하기 위해서 어떤 CFG 와, 해당 문법에서 를 도입하자. 또한 에서의 한 parse tree의 높이가 h일 때, 각 노드의 자식 수가 최대 b라고 하자.[2] 이 경우 트리의 leaf 노드의 수[3]는 최대 개이다. 따라서 문자열 s가 이면 해당 문자열을 만드는 parse tree의 높이는 h보다 커야 한다. 즉, 이는 긴 문자열은 필연적으로 높은 트리(깊은 유도)를 가져야 한다는 것을 의미한다. 이제 변수의 개수가 라고 할때, 트리의 경로를 따라가다 높이가 이상에 도달하면 어떠한 변수는 반드시 두 번 이상 등장해야 한다. 이 “두 번 등장한 변수”가 바로 pumping의 근거가 되는 것이다.
Applying the Pumping Lemma for CFLs
CFL에 대한 PL은 일반적인 PL과 마찬가지로 주어진 언어가 CFL이 아님을 증명하는데 사용할 수 있다. 예를 들어 아래와 같은 언어가 주어졌다고 가정하자:
위 언어는 어떤 문자열 w를 두 번 반복한 것들의 집합으로, 00, 0101, 1010, 11001100 등이 L에 속한다. 이 언어가 CFL이 아니라는 것은 아래와 같은 과정을 통해서 증명할 수 있다:
- L이 context-free라고 가정하자.
- Pumping Lemma에 의해 어떤 일정한 길이 p가 존재한다.
- Pumping Lemma를 적용하기 위해서는 를 만족하는 어떤 문자열 이 필요하다.
- 이에 따라 를 선택하며, 해당 문자열은 명백히 에 속한다.
- 문자열 에 대해 pumping lemma를 적용하면, 와 같이 나타내어지며, 아래 조건을 만족한다:
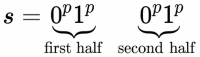
해당 단계 까지 진행하였다면 핵심은 모든 가능한 의 위치에 대해서 일 때 문자열이 L에 속하지 않음을 보이는 것이다. 이를 보이기 위해서는 가 에서 어디에 위치할 수 있는지를 세 가지로 나누어 설명해야 한다. Figure 1은 L의 문자열 구조이며, 케이스를 나눌 때의 이해를 돕기 위한 이미지이다. 이때 가능한 케이스는 가 첫 절반 안에 완전히 포함되는 경우,[4] 가 두 번째 절반 안에 완전히 포함되는 경우,[5] 가 중간 경계 를 걸치는 경우[6]이다. 이 세가지 경우만 고려하면 되는 이유는 이므로, 주어진 문자열 길이의 절반을 넘을 수 없기 때문이다. 각각의 경우를 살펴보면 아래와 같다:
- Case 1: 가 첫 절반 안에 완전히 포함되는 경우
- pumping을 하면 첫 절반이 변하고 두 번째 절반은 그대로 남는다.
- 예를 들어, 는 에 비해서 앞 절반의 길이나 내용이 달라졌으나, 뒤 절반은 변하지 않는다.
- 따라서 앞과 뒤가 더 이상 동일하지 않게되므로 이다.
- Case 2: 가 두 번째 절반 안에 완전히 포함되는 경우
- 이번엔 반대로, 두 번째 절반이 변하고 첫 절반은 그대로 남는다.
- 따라서 pumping 후에는 앞과 뒤가 더 이상 동일하지 않게되므로 이다.
- Case 3: 가 중간 경계 를 걸치는 경우
- 이 경우에 를 pump하면 “1 일부와 0 일부”가 동시에 변한다.
- 예를 들어, 일 때에는 앞 부분의 일부 1과 뒷 부분의 일부 0이 삭제되어서 앞과 뒤가 더 이상 동일하지 않는다.
- 따라서 이다.
따라서, 어떤 경우에도 pumping 후의 문자열은 L에 속하지 않는다. 이것은 Pumping Lemma의 조건 1을 위반하므로 모순이 발생한다.