Grammars

상위 문서: Regular Languages

개요

Grammar는 DFA나 NFA처럼 문자열을 소비하며 “인식(recognize)”하는 것이 아닌, 문자열을 생성(generate) 하는 시스템이다. 즉, grammar는 어떤 언어에 속하는 모든 문자열을 만들어내는 규칙들의 모음이다.

Classes of Grammars

문법은 아래와 같이 네가지로 구분된다:

1. Unrestricted Grammar: 아무 제약이 없는 일반적인 형태
2. Context-sensitive Grammar: 각 규칙에서 $|l|\le |r|$이다.
   • 이는 규칙을 적용하는 과정에서 문자열의 길이가 줄어들지 않음을 의미한다.
3. Context-free Grammar(CFG): 모든 규칙의 왼쪽이 단 하나의 비단말기라는 것을 의미한다.($l\in V$)
   • 문맥과 상관없이 하나의 비단말기만 보고 규칙을 적용할 수 있다.
   • PDA(푸시다운 오토마톤)과 동일한 계산 능력을 가진다.
4. Regular Grammar: CFG보다 더욱 단순한 형태이다. 기본적으로 CFG에 속한다.
   • 각 규칙은 $r=w$또는 $r=wB$꼴이며, 오른쪽 끝에 비단말기가 올 수 있다.
   • 이는 이름에서 짐작할 수 있듯이 정규언어와 정확히 동일한 클래스이다.

이때 Regular Grammar G가 정규언어와 정확히 동일한 클래스라는 것은 아래와 같은 의미이다:

L is regular 
$\iff L=L(G)$ for some regular grammar G

즉, 정규 언어와 정규 문법으로 생성 가능한 언어는 동일한 집합을 의미한다.

Definition of Grammars

Grammar는 아래와 같은 4-튜플($V,\mathrm{\Sigma },R,S$)을 통해서 정의된다:

1. $V$: 비단말기(nonterminal symbols)의 유한 집합
   • 예: $\{S,A,B\}$
   • 실제 문자열에 직접 등장하지는 않지만, 생성 과정에서 사용된다.
2. $\mathrm{\Sigma }$: 단말기(terminal symbols) 의 유한 집합
   • 예: $\{a,b,0,1\}$
   • 실제 언어의 문자열을 구성하는 기호들이며, $V$와 겹치지 않는다.
3. $R$: 규칙(rule)의 유한 집합
   • 각 규칙은 $l\to r$ 형태이고, $l,r\in (V\cup \mathrm{\Sigma })*$
   • $l$은 최소 하나의 비단말을 포함해야 하며, 규칙은 단말을 단말이나 다른 비단말로 치환하는 역할을 한다.
4. $S\in V$: 시작 기호(start symbol)

이때 두 집합 $V,\mathrm{\Sigma }$의 모든 기호를 섞어서 만들 수 있는 문자열 전체는 $(V\cup \mathrm{\Sigma })*$이다. 이는 sentential form이라고 불리며, 문법(Grammar)으로 문자열을 생성하는 과정에서 만들어지는 모든 문자열을 의미한다.

Derivations

문법을 사용해서 문자열을 생성하는 과정(derivation)은 아래와 같다:

• $u\Rightarrow v$: “u가 v를 한 단계 유도한다.”
  • 즉, 어떤 규칙 $l\to r$을 적용하여
    $u=w_{1}l{w}_2$인 문자열에서 $l$을 $r$로 바꾸면 $v=w_{1}r{w}_2$가 된다.
  • 즉, $u$ 안의 한 비단말기를 규칙에 따라 다른 형태로 치환하여 $v$를 얻는 것이다.

또한, 주어진 규칙 내에서 여러번 규칙을 적용하여 문자열 $v$를 얻을 수 있는데, 이를 기호로 나타내면 $u\Rightarrow *v$이다. 예를 들어, $u\Rightarrow u_1\Rightarrow u_2\Rightarrow \cdots \Rightarrow v$와 같은 방식이다. 이를 통해 문법 G가 생성하는 언어 $L(G)$는 아래와 같이 정의된다:

$L(G)=\{w\in \mathrm{\Sigma }*|S\Rightarrow *w\}$

Derivations Example 1

예를 들어, 아래와 같은 CFG $G=(V,\mathrm{\Sigma },R,S)$가 주어졌다고 가정하자:

• $V=\{S\}$
• $\mathrm{\Sigma }=\{0,1\}$
• $R=\{S\to ϵ,S\to 0S1\}$

위와 같은 grammar에서 문자열은 아래와 같이 유도된다:

$S\Rightarrow 0S1\Rightarrow 00S11\Rightarrow 000S1111\Rightarrow 000111$

즉, 같은 개수의 0과 1로 이루어진 문자열을 만들며, 이를 수식으로 표현하면 아래와 같다:

$L(G)=\{0^n{1}^n|n\ge 0\}$

Derivations Example 2

아래는 수학식(expression)을 생성하는 CFG $G=(V,\mathrm{\Sigma },R,S)$이다:

• $V=\{E,T,F\}$
• $\mathrm{\Sigma }=\{a,+,\times ,(,)\}$
• $R=\{E\to E+T|T,T\to T\times F|F,F\to (E)|a\}$

위 문법은 수학적인 식을 계층적으로 정의한다:

• E (식)은 하나 이상의 항(T)의 덧셈으로 이루어짐
• T(항)은 하나 이상의 인자(F)의 곱셈으로 이루어짐
• F(인자)는 괄호친 식(E) 이거나 단일 변수 a

아래는 위의 산술식 문법을 실제로 적용하여 $a+(a\times a)$ 문자열을 생성하는 예시이다:

$E\Rightarrow E+T\Rightarrow E+F\Rightarrow E+(E)\Rightarrow T+(E)\Rightarrow F+(E)$
$\Rightarrow F+(T)\Rightarrow F+(T\times F)\Rightarrow F+(F\times F)\Rightarrow F+(a\times F)$
$\Rightarrow F+(a\times a)\Rightarrow a+(a\times a)$

즉, 이 문법은 괄호, 곱셈, 덧셈을 포함한 올바른 산술식을 생성할 수 있다.

Leftmost Derivations

위의 예시들을 예리하게 살펴본다면, 하나의 문자열 $w$ 여러 가지 유도 방법(derivations)을 가지고 생성할 수 있다는 것을 알 수 있다. 따라서 이러한 이런 “유도 순서의 차이”로 생기는 혼란을 없애기 위해, 항상 왼쪽에 있는 비단말기부터 확장하는 규칙을 사용하며, 이를 leftmost derivation(좌측 유도)이라고 한다.

예를 들어, 아래는 위의 산술식을 생성하는 grammar를 leftmost derivation을 사용하여 문자열 $a+(a\times a)$를 유도한 것이다:

$E\Rightarrow E+T\Rightarrow T+T\Rightarrow F+T\Rightarrow a+F\Rightarrow a+(E)$
$\Rightarrow a+(T)\Rightarrow a+(T\times F)\Rightarrow a+(F\times F)\Rightarrow F+(a\times F)$
$\Rightarrow a+(a\times F)\Rightarrow a+(a\times a)$

Parse Trees

Parse Trees는 유도 과정을 트리(tree) 형태로 표현한 것이다. CFG에 대한 parse tree는 아래와 같은 특징을 가진다:

1. CFG에 대한 parse tree는 ordered tree이다.
2. Internal nodes는 비단말기이다.
3. Leaf nodes들은 단말기이다.
4. 각 internal nodes는 문법의 규칙 $A\to r$에 따라 자식 노드를 가지며, 자식 노드의 수는 $|r|$과 같다.

Figure 1. Parse Trees Example 1

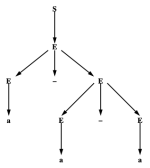
예를 들어 CFG $G=(V,\mathrm{\Sigma },R,S)$가 아래와 같이 주어졌다고 가정하자.

• $V=\{S,E\}$
• $\mathrm{\Sigma }=\{a,-\}$
• $R=\{S\to E,E\to E-E,E\to a\}$

위와 같은 grammar에 대해 문자열 $a-a-a$를 유도하는 parse tree는 figure 1과 같다. 이때 하나의 leftmost derivation은 하나의 parse tree와 정확히 1:1로 대응한다. Figure 1에 나타난 유도과정은 아래와 같은 leftmost derivation과 대응된다:

$S\Rightarrow E\Rightarrow E-E\Rightarrow a-E$
$\Rightarrow a-E-E\Rightarrow a-a-E\Rightarrow a-a-a$

Figure 2. Parse Trees Example 2

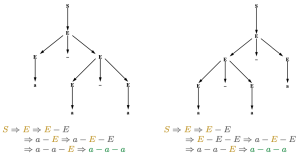
Figure 2는 다르게 parse tree가 구성되었다면, 이와 대응되는 leftmost derivation또한 달라진다는 것을 보여준다.

Ambiguity

하나의 문자열을 생성할 때, 여러 개의 트리로 표현될 수 있다면 해당 문법은 “모호하다(ambiguous)”고 한다. 예를 들어, figure 2에 주어진 서로 다른 트리는 같은 문법을 통해 같은 문자열 $a-a-a$를 서로 다른 순서를 통해 유도하는 것을 보여준다. 따라서 해당 문법은 모호하다.

Context-Free Languages

CFL(Context-Free Languages)이란 어떤 CFG로부터 생성될 수 있는 언어이다. 이는 아래와 같이 나타내어 진다:

A language L is context-free 
$\iff L=L(G)$ for some CFG G

이때 모든 정규언어는 context-free이다. 이는 모든 정규 언어는 항상 regular grammar로 표현될 수 있는데, 모든 정규 문법은 문맥자유문법의 특수한 형태이기 때문이다. 즉, 아래와 같은 명제가 성립한다.

Regular Languages $\subseteq$ Context-Free Languages

이는 정규언어보다 CFL의 표현력이 더 강하다는 것을 의미한다. 예를 들어 $L=\{0^n{1}^n|n\ge 0\}$과 같은 언어는 정규언어가 아니지만 CFG로는 표현 가능하다. 따라서 아래와 같은 명제가 성립한다.

$CFL\cap RegularLanguage\subseteq CFL$

이는 어떠한 언어가 CFL이기도 하면서, 정규 언어이기도 한다면 CFL에 속한다는 것을 의미한다. 또한 아래와 같은 명제가 성립한다:

The class of context-free languages is closed under $\cup ,\circ ,*$.

이는 정규언어와 마찬가지로 CFL $L_1,L_2$에 대해, $L_1\cup L_2,L_1{L}_2,L_1*$도 모두 CFL이라는 것을 의미한다.

Chomsky Normal Form

CNF(Chomsky Normal Form)는 CFG를 더욱 간단하고 증명하기 쉽게 바꾼 표준 형식이다.
CNF(Chomsky Normal Form)에 대한 자세한 정보는 해당 문서를 참조해 주십시오.

CYK Algorithm

CYK(Cocke–Younger–Kasami) 알고리즘은 CFL(Context-Free Language)를 인식하기 위한 동적 프로그래밍 기반의 알고리즘이다.
자세한 내용은 CYK Algorithm 문서를 참조해 주십시오.

Pushdown Automaton

정규 언어를 다루기 위해서는 Finite Automaton으로 충분하지만, 그보다 더 일반적인 언어인 CFG를 다루기 위해서는 Pushdown Automaton이 사용된다.
자세한 설명은 Pushdown Automaton 문서를 참조해 주십시오.