Topological Sorting: 두 판 사이의 차이
새 문서: 분류:알고리즘 설계와 분석 분류:컴퓨터 공학 상위 문서: 알고리즘 설계와 분석 ==개요== 위상 정렬(Topological Sorting)은 사이클이 없는 방향 그래프(DAG)에 대해서만 가능하다. 이때 위상 정렬이란 모든 간선 (u → v)에 대해, u가 항상 v보다 먼저 나와야 한다는 것을 의미한다. 예를 들어 figure 1은 주어진 왼쪽 그래프의 간선의 방향이... |
편집 요약 없음 |
||
| 4번째 줄: | 4번째 줄: | ||
==개요== | ==개요== | ||
[[파일:Figure 1. 위상 정렬 예시.png|섬네일|Figure 1. 위상 정렬 예시]] | |||
위상 정렬(Topological Sorting)은 사이클이 없는 방향 그래프(DAG)에 대해서만 가능하다. 이때 위상 정렬이란 모든 간선 (u → v)에 대해, u가 항상 v보다 먼저 나와야 한다는 것을 의미한다. 예를 들어 figure 1은 주어진 왼쪽 그래프의 간선의 방향이 “왼쪽에서 오른쪽”으로 진행되도록 배열하여 오른쪽과 같이 배치된 것을 볼 수 있다. | 위상 정렬(Topological Sorting)은 사이클이 없는 방향 그래프(DAG)에 대해서만 가능하다. 이때 위상 정렬이란 모든 간선 (u → v)에 대해, u가 항상 v보다 먼저 나와야 한다는 것을 의미한다. 예를 들어 figure 1은 주어진 왼쪽 그래프의 간선의 방향이 “왼쪽에서 오른쪽”으로 진행되도록 배열하여 오른쪽과 같이 배치된 것을 볼 수 있다. | ||
==Applying Toplogical Sorting== | ==Applying Toplogical Sorting== | ||
[[파일:Figure 2. 의류 착용 제약 조건 그래프.png|섬네일|Figure 2. 의류 착용 제약 조건 그래프]] | |||
위상 정렬은 “주어진 제약조건을 만족하면서 해야 할 일들을 어떤 순서로 수행할 것인가?”와 같은 스케줄링(scheduling) 문제에서 매우 자주 사용된다. 예를 들어 figure 2는 옷을 입을 때의 순서에 대한 제약 조건을 그래프로 표현한 것이다. 이를 위상 정렬로 표현함으로서 모든 의류의 올바른 착용 순서를 얻을 수 있다. | 위상 정렬은 “주어진 제약조건을 만족하면서 해야 할 일들을 어떤 순서로 수행할 것인가?”와 같은 스케줄링(scheduling) 문제에서 매우 자주 사용된다. 예를 들어 figure 2는 옷을 입을 때의 순서에 대한 제약 조건을 그래프로 표현한 것이다. 이를 위상 정렬로 표현함으로서 모든 의류의 올바른 착용 순서를 얻을 수 있다. | ||
[[파일:Figure 3. DNA 패턴 분석.png|섬네일|Figure 3. DNA 패턴 분석]] | |||
예를 들어, DNA 서열 재조합(DNA sequence assembly)에서 figure 3와 같은 상황을 가정하자. DNA를 읽을 때, 전체 서열이 아니라 “부분(fragment)” 단위로 읽으며, 각 조각들을 겹치는 순서대로 이어붙여야 전체 서열을 복원할 수 있다. 이 조각들을 그래프의 노드로 두고, “어떤 조각이 다른 조각보다 왼쪽"이라는 순서 제약을 간선으로 표현하면 DAG가 된다. 이 DAG를 위상 정렬하면, 모든 조각이 일관된 순서로 이어진 완전한 DNA 서열을 얻을 수 있다. | 예를 들어, DNA 서열 재조합(DNA sequence assembly)에서 figure 3와 같은 상황을 가정하자. DNA를 읽을 때, 전체 서열이 아니라 “부분(fragment)” 단위로 읽으며, 각 조각들을 겹치는 순서대로 이어붙여야 전체 서열을 복원할 수 있다. 이 조각들을 그래프의 노드로 두고, “어떤 조각이 다른 조각보다 왼쪽"이라는 순서 제약을 간선으로 표현하면 DAG가 된다. 이 DAG를 위상 정렬하면, 모든 조각이 일관된 순서로 이어진 완전한 DNA 서열을 얻을 수 있다. | ||
2025년 10월 16일 (목) 05:50 기준 최신판
상위 문서: 알고리즘 설계와 분석
개요
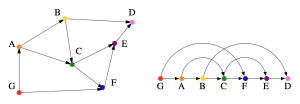
위상 정렬(Topological Sorting)은 사이클이 없는 방향 그래프(DAG)에 대해서만 가능하다. 이때 위상 정렬이란 모든 간선 (u → v)에 대해, u가 항상 v보다 먼저 나와야 한다는 것을 의미한다. 예를 들어 figure 1은 주어진 왼쪽 그래프의 간선의 방향이 “왼쪽에서 오른쪽”으로 진행되도록 배열하여 오른쪽과 같이 배치된 것을 볼 수 있다.
Applying Toplogical Sorting
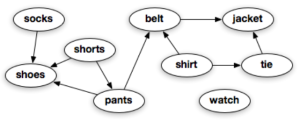
위상 정렬은 “주어진 제약조건을 만족하면서 해야 할 일들을 어떤 순서로 수행할 것인가?”와 같은 스케줄링(scheduling) 문제에서 매우 자주 사용된다. 예를 들어 figure 2는 옷을 입을 때의 순서에 대한 제약 조건을 그래프로 표현한 것이다. 이를 위상 정렬로 표현함으로서 모든 의류의 올바른 착용 순서를 얻을 수 있다.

예를 들어, DNA 서열 재조합(DNA sequence assembly)에서 figure 3와 같은 상황을 가정하자. DNA를 읽을 때, 전체 서열이 아니라 “부분(fragment)” 단위로 읽으며, 각 조각들을 겹치는 순서대로 이어붙여야 전체 서열을 복원할 수 있다. 이 조각들을 그래프의 노드로 두고, “어떤 조각이 다른 조각보다 왼쪽"이라는 순서 제약을 간선으로 표현하면 DAG가 된다. 이 DAG를 위상 정렬하면, 모든 조각이 일관된 순서로 이어진 완전한 DNA 서열을 얻을 수 있다.
Topological Sorting via DFS
위상 정렬은 DFS 알고리즘을 통해 구현할 수 있다. DFS 중에 Back Edge가 존재하지 않으면, 사이클이 존재하지 않으므로 DAG라는 것을 의미한다. 따라서 DFS로 DAG를 탐색하면서 각 정점의 처리 완료 시점(finished time)을 기록하면, 이 역순(reverse order)이 바로 위상 정렬이 된다. 이는 아래와 같은 구현 원리를 가진다:
- DFS를 수행한다.
- 어떤 노드의 인접 노드 탐색이 모두 끝났을 때[1] 그 노드를 스택에 push한다.
- 모든 노드에 대해 이 과정을 수행한 뒤, 스택을 뒤집으면 위상 정렬 순서가 된다.
이에 대해 직관적으로 보면, 간선 (x, y)가 있을 때, x의 탐색이 y보다 먼저 시작되므로 x가 y보다 나중에 처리 완료된다는 것이다. 따라서 이에 대한 완료 시점을 역순으로 나열하면 모든 간선이 왼쪽에서 오른쪽 방향이 된다. 이를 좀 더 자세히 살펴보기 위해, 각 간선(x, y)이 어떤 상태에 있는가 분석할 수 있다.
- If y is undiscovered
- y는 아직 방문하지 않아 DFS는 y를 먼저 탐색한다.
- 따라서 y가 먼저 완료되고 x가 나중에 완료된다.
- 위상 정렬에서 x가 y보다 앞에 위치한다.
- If y is discovered but not completed
- y는 아직 처리 중이며, 이에 따라 간선 (x, y)는 back edge이다.
- 이때 back edge는 사이클을 의미하므로, DAG에서는 존재할 수 없다.
- If y is completed
- y의 탐색이 이미 끝났고, 이는 y는 x보다 일찍 완료된 상태라는 것을 의미한다.
- 위상 정렬에서 x가 y보다 앞에 위치한다.
이 세 가지 경우 모두 DAG의 위상 정렬 조건을 만족한다.
Topological Sorting Implementation
아래는 DFS를 이용한 위상 정렬의 핵심 구조를 보여주는 코드이다:
void process_vertex_late(int v) {
push(&sorted, v);
}
위 코드는 DFS에서 한 정점 v의 모든 인접 노드를 다 탐색하고 난 “후처리 단계(late processing)” 에 실행되는 함수이다. 즉, 정점의 모든 outgoing edge(출발 간선) 이 끝난 시점에 실행되며, v를 sorted 스택에 push한다. 이때 DFS 완료 후, 스택을 뒤집으면 위상 정렬 순서가 된다.
void process_edge(int x, int y) {
int class;
class = edge_classification(x, y);
if (class == BACK) {
printf("Warning: directed cycle found, not a DAG\n");
}
}
위는 판단하고자 하는 방향 그래프에서 해당 간선의 종류를 판단하는 함수이다. 이는 해당 그래프에 back edge가 존재하는지 판단하여 그래프가 DAG가 아니라면 이에 대해 경고하는 안전 장치 역할을 한다. 위 함수들을 통해서 아래와 같이 위상 정렬 알고리즘이 구현된다.
void topsort(graph *g) {
int i;
init_stack(&sorted); //위상 정렬 결과를 저장할 스택 초기화
for (i = 1; i <= g->nvertices; i++) {
if (!discovered[i]) {
dfs(g, i);
}
}
print_stack(&sorted); /* report topological order */
}
Kahn’s Algorithm
아래는 DFS가 아닌, 진입차수(indegree) 를 이용한 Kahn’s algorithm 방식이다.
void toposort(graph *g, int sorted[]) {
int indegree[MAXV+1]; /* indegree of each vertex */
queue zeroin; /* vertices of indegree 0 */
int x, y; /* current and next vertex */
int i, j; /* counters */
edgenode *p; /* temporary pointer */
compute_indegrees(g, indegree);
init_queue(&zeroin);
for (i = 1; i <= g->nvertices; i++) {
if (indegree[i] == 0) {
enqueue(&zeroin, i);
}
}
j = 0;
while (!empty_queue(&zeroin)) {
j = j + 1;
x = dequeue(&zeroin);
sorted[j] = x;
p = g->edges[x];
while (p != NULL) {
y = p->y;
indegree[y]--;
if (indegree[y] == 0) {
enqueue(&zeroin, y);
}
p = p->next;
}
}
if (j != g->nvertices) {
printf("Not a DAG -- only %d vertices found\n", j);
}
}
void compute_indegrees(graph *g, int in[]) {
int i; /* counter */
edgenode *p; /* temporary pointer */
for (i = 1; i <= g->nvertices; i++) {
in[i] = 0;
}
for (i = 1; i <= g->nvertices; i++) {
p = g->edges[i];
while (p != NULL) {
in[p->y]++;
p = p->next;
}
}
}
각주
- ↑ 즉, processed = true인 상태이다.