Binary Search Tree: 두 판 사이의 차이
새 문서: 분류:알고리즘 설계와 분석 분류:컴퓨터 공학 상위 문서: Data Structures ==개요== 해당 문서는 이진 트리(binary tree)의 한 종류인 이진 탐색 트리(binary search tree)에 대해서 다룬다. 먼저, 이진 트리는 루트(root)를 가진 트리 구조이며, 각 노드는 최대 두 개의 자식을 가진다. 이때 자식 노드는 왼쪽(left child)또는 오른쪽(right child)으로 구분... |
|||
| (같은 사용자의 중간 판 9개는 보이지 않습니다) | |||
| 4번째 줄: | 4번째 줄: | ||
==개요== | ==개요== | ||
[[파일:Figure 1. Binary Search Tree.jpg|섬네일|258x258픽셀|Figure 1. Binary Search Tree]] | |||
해당 문서는 이진 트리(binary tree)의 한 종류인 이진 탐색 트리(binary search tree)에 대해서 다룬다. 먼저, 이진 트리는 루트(root)를 가진 트리 구조이며, 각 노드는 최대 두 개의 자식을 가진다. 이때 자식 노드는 왼쪽(left child)또는 오른쪽(right child)으로 구분된다. 이러한 이진 트리 구조는 figure 1에 잘 나타나 있다. 그 중에서도 이진 탐색 트리는 자료 구조의 한 종류로, 사전(dictionary) 연산(검색, 삽입, 삭제, 최소값, 최대값, 후속자/전임자 찾기)을 효율적으로 수행할 수 있게 한다. | 해당 문서는 이진 트리(binary tree)의 한 종류인 이진 탐색 트리(binary search tree)에 대해서 다룬다. 먼저, 이진 트리는 루트(root)를 가진 트리 구조이며, 각 노드는 최대 두 개의 자식을 가진다. 이때 자식 노드는 왼쪽(left child)또는 오른쪽(right child)으로 구분된다. 이러한 이진 트리 구조는 figure 1에 잘 나타나 있다. 그 중에서도 이진 탐색 트리는 자료 구조의 한 종류로, 사전(dictionary) 연산(검색, 삽입, 삭제, 최소값, 최대값, 후속자/전임자 찾기)을 효율적으로 수행할 수 있게 한다. | ||
| 46번째 줄: | 47번째 줄: | ||
===Maximum and Minimum=== | ===Maximum and Minimum=== | ||
[[파일:Figure 2. Min-Max.jpg|섬네일|250x250픽셀|Figure 2. Min-Max]] | |||
이진 탐색 트리에서 최솟값/최댓값을 탐색하는 것은 매우 쉽다. 최솟값은 가장 왼쪽에 위치한 노드이며, 최댓값은 가장 오른쪽에 위치한 노드이기 때문이다. 따라서 원리는 같으므로, 최솟값을 탐색하는 코드만 언급한다: | 이진 탐색 트리에서 최솟값/최댓값을 탐색하는 것은 매우 쉽다. 최솟값은 가장 왼쪽에 위치한 노드이며, 최댓값은 가장 오른쪽에 위치한 노드이기 때문이다. 따라서 원리는 같으므로, 최솟값을 탐색하는 코드만 언급한다: | ||
<syntaxhighlight lang="c"> | <syntaxhighlight lang="c"> | ||
| 65번째 줄: | 67번째 줄: | ||
===Predecessor/Successor=== | ===Predecessor/Successor=== | ||
<gallery widths="300" heights="300"> | |||
파일:Figure 3. Predecessor-Successor EXAMPLE.jpg|Figure 3. Predecessor-Successor Case 1 | |||
파일:Figure 4. Predecessor-Successor Case 2.jpg|Figure 4. Predecessor-Successor Case 2.jpg | |||
</gallery> | |||
어떤 sorted list 자료구조의 predecessor와 successor의 정의는 아래와 같다: | |||
* Predecessor: 어떤 노드 X의 바로 앞 원소. | |||
* Successor: 어떤 노드 X의 바로 뒤 원소. | |||
이를 이진 탐색 트리에 확장시키면, 어떤 노드 X가 두 자식을 가진다고 할 때 아래와 같이 정의된다: | |||
* Predecessor: X의 왼쪽 서브트리의 최대값 | |||
* Successor: X의 오른쪽 서브트리의 최솟값 | |||
figure 2에는 X의 predecessor와 successor가 화살표로 표시되어 있다. 하지만 figure 3와 같이 노드 X가 왼쪽 자식 노드를 가지지 않은 경우에는 predecessor를 동일한 방식으로 찾을 수 없다. 하지만 해당 경우에도 직관적으로 찾을 수 있는데, predecessor는 첫 번째 왼쪽 조상 노드이다. 이러한 직관은 오른쪽 자식을 가지지 않은 경우의 successor를 찾는 경우에도 적용될 수 있다. 이 경우 successor는 첫 번째 오른쪽 조상 노드이다. | |||
===In-Order Traversal=== | |||
[[파일:Figure 5. In-Order Traversal.jpg|섬네일|298x298px|Figure 5. In-Order Traversal]] | |||
In-Order Traversal은 이진 탐색 트리를 오름차순으로 순회하는 탐색법이다. 이는 아래와 같은 재귀적인 메커니즘을 가진다: | |||
# 왼쪽 서브트리를 먼저 방문 | |||
# 그 다음 현재 노드를 방문 | |||
# 마지막으로 오른쪽 서브트리를 방문 | |||
이는 아래와 같은 코드를 통해 구현된다: | |||
<syntaxhighlight lang="c"> | |||
void traverse_tree(tree *l) { | |||
if (l != NULL) { | |||
traverse_tree(l->left); | |||
process_item(l->item); | |||
traverse_tree(l->right); | |||
} | |||
} | |||
</syntaxhighlight> | |||
이러한 메커니즘은 figure 4와 같은 이진 탐색 트리를 A,B,C,D,E,F,G,H의 순서로 순회한다. 이때 시간 복잡도는 각 노드 방문에 O(1) 시간이 소요되고 총 n개의 노드를 방문하므로 O(n)의 시간복잡도가 소요된다. | |||
===Tree Insertion/Deletion=== | |||
새로운 원소 x를 트리에 삽입하고자 할때에는 먼저 이진 탐색을 해서 삽입할 위치인 NIL(=NULL) 포인터에 도달하면, 그 위치를 새 노드로 교체한다. 즉, 이는 검색하는 알고리즘과 같은 맥락의 논리를 사용하고 마지막에 새로운 노드를 추가하는 것만 다르므로, 재귀적으로 구현할 수 있다. 이는 아래와 같이 구현된다: | |||
<syntaxhighlight lang="c"> | <syntaxhighlight lang="c"> | ||
void insert_tree(tree **l, item_type x, tree *parent) { | |||
tree *p; /* 새 노드를 가리킬 포인터 */ | |||
if (*l == NULL) { //NULL 포인터에 도달하였으므로 해당 위치에 삽입 | |||
p = malloc(sizeof(tree)); | |||
p->item = x; | |||
p->left = p->right = NULL; | |||
p->parent = parent; | |||
*l = p; // 현재 NULL 위치에 새 노드 연결 | |||
return; | |||
} | |||
if (x < (*l)->item) { | |||
insert_tree(&((*l)->left), x, *l); // 왼쪽에 서브 트리에 삽입 | |||
} else { | |||
insert_tree(&((*l)->right), x, *l); // 오른쪽에 서브 트리에 삽입 | |||
} | |||
} | |||
</syntaxhighlight> | </syntaxhighlight> | ||
< | 하지만 트리에서 어떤 노드를 삭제하는 것은 더욱 까다롭다. 노드를 삭제하는 작업은 삭제하려는 노드의 위치에 따라 아래와 같은 세 가지 경우로 나뉜다: | ||
# 삭제 노드가 leaf 노드: 단순히 부모의 삭제 노드에 대한 포인터를 NULL로 설정한다. | |||
# 삭제 노드가 자식 1개: 삭제 노드의 자식을 부모의 삭제 노드에 대한 포인터에 직접 연결한다. | |||
# 삭제 노드가 자식 2개: 복잡한 작업을 요구한다. | |||
## 삭제할 노드의 successor 또는 predecessor를 찾는다. | |||
## 삭제 노드의 값을 successor(또는 predecessor)의 값으로 교체한다. | |||
## 그 다음 successor(또는 predecessor) 노드를 삭제한다.<ref>이 노드는 자식이 최대 1개뿐이므로 삭제가 쉽다.</ref> | |||
이는 figure 6를 참조하여 그 원리를 쉽게 알아낼 수 있다. | |||
</ | ==Balanced Binary Search Trees== | ||
< | 이진 탐색 트리를 사전 자료구조를 구현하는 데에 사용하면 모든 6가지 사전 연산(삽입·삭제·검색·최소·최대·전임/후임)이 트리의 높이 h에 비례하여 O(h) 시간이 걸린다. 이때 트리가 최적으로 구성이 되었다면(트리가 perfectly blanced라면) <math>h \approx log(n)</math> 수준이다. 이는 아래와 같은 수식을 통해서 알 수 있다: | ||
<math>\sum^{\lfloor log(n)\rfloor}_{i = 0}2^i\approx n</math> | |||
하지만 insert(1), insert(2), insert(3), ...과 같은 순서대로 삽입하였을 경우에는 트리가 한쪽으로 주욱 늘어진 사슬 모양이 된다. 이는 이진 탐색 트리가 최악으로 구성된 경우인데, 트리의 높이가 O(n)과 같이 선형으로 커지기 때문이다. 따라서 단순 이진 탐색 트리는 삽입이 불운한 순서로 이루어질 경우에는 효율이 급격히 안 좋아질 수 있다는 단점이 있다. | |||
</ | 하지만 무작위한 삽입 순서로 만들어진 이진 탐색 트리는 평균적으로 높이가 <math>\Theta(log(n))</math>이 된다. 이는 새로운 키가 삽입될 때, 절반 정도 확률로 트리의 중앙값(median)에 가까운 위치로 들어가며, 이는 분할이 고르게 일어난다는 것을 의미한다. | ||
Perfectly Balanced 트리는 이론적으로는 이상적이지만, 실제로는 유지하기 어렵다. 그 이유는 어떠한 Perfectly Balanced 트리에 새로운 키를 삽입하고 잘 할 때에는 이를 유지하기 위해 모든 노드의 위치를 재조정해야 하기 때문이다. 이 과정에 드는 비용은 <math>\Theta(log(n))</math>으로 배보다 배꼽이 더 큰 격이다. | |||
==각주== | ==각주== | ||
2025년 9월 24일 (수) 21:11 기준 최신판
상위 문서: Data Structures
개요

해당 문서는 이진 트리(binary tree)의 한 종류인 이진 탐색 트리(binary search tree)에 대해서 다룬다. 먼저, 이진 트리는 루트(root)를 가진 트리 구조이며, 각 노드는 최대 두 개의 자식을 가진다. 이때 자식 노드는 왼쪽(left child)또는 오른쪽(right child)으로 구분된다. 이러한 이진 트리 구조는 figure 1에 잘 나타나 있다. 그 중에서도 이진 탐색 트리는 자료 구조의 한 종류로, 사전(dictionary) 연산(검색, 삽입, 삭제, 최소값, 최대값, 후속자/전임자 찾기)을 효율적으로 수행할 수 있게 한다.
이진 탐색 트리의 중요한 특징은 각 노드 x에 대해 왼쪽 서브 트리의 모든 키 값들은 x보다 작으며, 오른쪽 서브트리의 모든 키 값들은 x보다 크다는 것이다. 이는 figure 1에 잘 나타나 있다. 따라서 어떤 값이든지 "왼쪽으로 갈지, 오른쪽으로 갈지"를 비교를 통해 정할 수 있고, 그 과정에서 원하는 키를 찾을 수 있다. 이는 이진 탐색과 비슷한 원리를 사용하므로, 시간복잡도면에서 효율적이다.
Implementing Binary Search Trees
C언어에서 이진 탐색 트리는 아래와 같이 구현될 수 있다:
typedef struct tree {
item_type item; /* 데이터 항목 */
struct tree *parent; /* 부모 노드 포인터 */
struct tree *left; /* 왼쪽 자식 포인터 */
struct tree *right; /* 오른쪽 자식 포인터 */
} tree;
이때 부모 노드에 대한 포인터는 선택 사항이다. 왜냐하면 여러 연산을 구현할 때 순회 과정에서 스택에 부모 노드를 저장하면, 굳이 구조체에 parent 필드를 두지 않아도 되기 때문이다.
Searching in a Binary Tree
이진 탐색 트리에서 특정한 키 값 x를 가진 노드를 찾고자 할 때에는 아래와 같은 코드를 이용한다:
tree *search_tree(struct tree *l, item_type x) {
if (l == NULL) {
return(NULL);
}
if (l->item == x) {
return(l);
}
if (x < l->item) {
return(search_tree(l->left, x));
} else {
return(search_tree(l->right, x));
}
}
이는 아래와 같이 작동한다:
- 현재 노드 l이 NULL이면 탐색 실패 → NULL 반환.
- 현재 노드의 값이 x와 같으면 탐색 성공 → 해당 노드 반환.
- x가 현재 노드보다 작으면 왼쪽 서브트리에서 재귀 탐색.
- x가 더 크면 오른쪽 서브트리에서 재귀 탐색.
즉, 해당 함수는 재귀적으로 작동하며, 이를 통해 시간 복잡도를 추측할 수 있다. 최악의 상황은 x가 존재하지 않아 NULL을 반환할 때까지 함수가 재귀적으로 작동하거나, 트리의 레벨이 가장 높은 leaf 노드에 x 키값이 존재하는 경우이다. 즉, 해당 알고리즘의 시간 복잡도는 트리의 높이인 h에 비례하므로 O(h)이다.
이때 중요한 것은 해당 트리의 모양에 따라 시간 복잡도가 달라진다는 것이다. 만약 트리가 최적으로 구성된 균형 트리라면 의 시간복잡도를 가진다. 하지만 노드가 최대 하나의 자식만을 가지는 편향 트리라면 의 시간복잡도를 가진다.
Maximum and Minimum
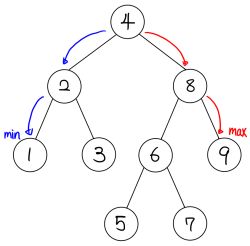
이진 탐색 트리에서 최솟값/최댓값을 탐색하는 것은 매우 쉽다. 최솟값은 가장 왼쪽에 위치한 노드이며, 최댓값은 가장 오른쪽에 위치한 노드이기 때문이다. 따라서 원리는 같으므로, 최솟값을 탐색하는 코드만 언급한다:
tree *find_minimum(struct tree *t) {
tree *min;
if (t == NULL) {
return(NULL);
}
min = t;
while (min->left != NULL) {
min = min->left;
}
return(min);
}
해당 코드의 원리는 간단하다. 포인터 t가 NULL이면 유효한 이진 탐색 트리가 아니므로 실패한다. 그렇지 않다면 while문을 이용하여 노드의 왼쪽 자식이 없을 때까지 반복하여 내려가고, 최종적으로 가장 왼쪽 노드를 반환한다. 만약 최댓값을 찾고 싶다면, 노드의 오른쪽 자식이 없을 때까지 반복하여 내려가면 된다.
해당 코드의 시간 복잡도는 키값 탐색과 같이 트리의 높이 h에 비례하므로 O(h)이다.
Predecessor/Successor
-
Figure 3. Predecessor-Successor Case 1
-
Figure 4. Predecessor-Successor Case 2.jpg
어떤 sorted list 자료구조의 predecessor와 successor의 정의는 아래와 같다:
- Predecessor: 어떤 노드 X의 바로 앞 원소.
- Successor: 어떤 노드 X의 바로 뒤 원소.
이를 이진 탐색 트리에 확장시키면, 어떤 노드 X가 두 자식을 가진다고 할 때 아래와 같이 정의된다:
- Predecessor: X의 왼쪽 서브트리의 최대값
- Successor: X의 오른쪽 서브트리의 최솟값
figure 2에는 X의 predecessor와 successor가 화살표로 표시되어 있다. 하지만 figure 3와 같이 노드 X가 왼쪽 자식 노드를 가지지 않은 경우에는 predecessor를 동일한 방식으로 찾을 수 없다. 하지만 해당 경우에도 직관적으로 찾을 수 있는데, predecessor는 첫 번째 왼쪽 조상 노드이다. 이러한 직관은 오른쪽 자식을 가지지 않은 경우의 successor를 찾는 경우에도 적용될 수 있다. 이 경우 successor는 첫 번째 오른쪽 조상 노드이다.
In-Order Traversal
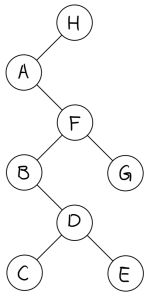
In-Order Traversal은 이진 탐색 트리를 오름차순으로 순회하는 탐색법이다. 이는 아래와 같은 재귀적인 메커니즘을 가진다:
- 왼쪽 서브트리를 먼저 방문
- 그 다음 현재 노드를 방문
- 마지막으로 오른쪽 서브트리를 방문
이는 아래와 같은 코드를 통해 구현된다:
void traverse_tree(tree *l) {
if (l != NULL) {
traverse_tree(l->left);
process_item(l->item);
traverse_tree(l->right);
}
}
이러한 메커니즘은 figure 4와 같은 이진 탐색 트리를 A,B,C,D,E,F,G,H의 순서로 순회한다. 이때 시간 복잡도는 각 노드 방문에 O(1) 시간이 소요되고 총 n개의 노드를 방문하므로 O(n)의 시간복잡도가 소요된다.
Tree Insertion/Deletion
새로운 원소 x를 트리에 삽입하고자 할때에는 먼저 이진 탐색을 해서 삽입할 위치인 NIL(=NULL) 포인터에 도달하면, 그 위치를 새 노드로 교체한다. 즉, 이는 검색하는 알고리즘과 같은 맥락의 논리를 사용하고 마지막에 새로운 노드를 추가하는 것만 다르므로, 재귀적으로 구현할 수 있다. 이는 아래와 같이 구현된다:
void insert_tree(tree **l, item_type x, tree *parent) {
tree *p; /* 새 노드를 가리킬 포인터 */
if (*l == NULL) { //NULL 포인터에 도달하였으므로 해당 위치에 삽입
p = malloc(sizeof(tree));
p->item = x;
p->left = p->right = NULL;
p->parent = parent;
*l = p; // 현재 NULL 위치에 새 노드 연결
return;
}
if (x < (*l)->item) {
insert_tree(&((*l)->left), x, *l); // 왼쪽에 서브 트리에 삽입
} else {
insert_tree(&((*l)->right), x, *l); // 오른쪽에 서브 트리에 삽입
}
}
하지만 트리에서 어떤 노드를 삭제하는 것은 더욱 까다롭다. 노드를 삭제하는 작업은 삭제하려는 노드의 위치에 따라 아래와 같은 세 가지 경우로 나뉜다:
- 삭제 노드가 leaf 노드: 단순히 부모의 삭제 노드에 대한 포인터를 NULL로 설정한다.
- 삭제 노드가 자식 1개: 삭제 노드의 자식을 부모의 삭제 노드에 대한 포인터에 직접 연결한다.
- 삭제 노드가 자식 2개: 복잡한 작업을 요구한다.
- 삭제할 노드의 successor 또는 predecessor를 찾는다.
- 삭제 노드의 값을 successor(또는 predecessor)의 값으로 교체한다.
- 그 다음 successor(또는 predecessor) 노드를 삭제한다.[1]
이는 figure 6를 참조하여 그 원리를 쉽게 알아낼 수 있다.
Balanced Binary Search Trees
이진 탐색 트리를 사전 자료구조를 구현하는 데에 사용하면 모든 6가지 사전 연산(삽입·삭제·검색·최소·최대·전임/후임)이 트리의 높이 h에 비례하여 O(h) 시간이 걸린다. 이때 트리가 최적으로 구성이 되었다면(트리가 perfectly blanced라면) 수준이다. 이는 아래와 같은 수식을 통해서 알 수 있다:
하지만 insert(1), insert(2), insert(3), ...과 같은 순서대로 삽입하였을 경우에는 트리가 한쪽으로 주욱 늘어진 사슬 모양이 된다. 이는 이진 탐색 트리가 최악으로 구성된 경우인데, 트리의 높이가 O(n)과 같이 선형으로 커지기 때문이다. 따라서 단순 이진 탐색 트리는 삽입이 불운한 순서로 이루어질 경우에는 효율이 급격히 안 좋아질 수 있다는 단점이 있다.
하지만 무작위한 삽입 순서로 만들어진 이진 탐색 트리는 평균적으로 높이가 이 된다. 이는 새로운 키가 삽입될 때, 절반 정도 확률로 트리의 중앙값(median)에 가까운 위치로 들어가며, 이는 분할이 고르게 일어난다는 것을 의미한다.
Perfectly Balanced 트리는 이론적으로는 이상적이지만, 실제로는 유지하기 어렵다. 그 이유는 어떠한 Perfectly Balanced 트리에 새로운 키를 삽입하고 잘 할 때에는 이를 유지하기 위해 모든 노드의 위치를 재조정해야 하기 때문이다. 이 과정에 드는 비용은 으로 배보다 배꼽이 더 큰 격이다.
각주
- ↑ 이 노드는 자식이 최대 1개뿐이므로 삭제가 쉽다.

