Cache: 두 판 사이의 차이
편집 요약 없음 |
|||
| (같은 사용자의 중간 판 9개는 보이지 않습니다) | |||
| 7번째 줄: | 7번째 줄: | ||
캐시가 필요한 핵심적인 이유는, CPU 성능의 발전 속도와 DRAM 메모리 성능의 발전 속도의 차이이다. CPU 성능은 매년 약 55% 향상되지만, DRAM 메모리 성능은 매년 약 7% 향상된다. 이는 CPU와 메모리 사이의 병목 현상을 일으키는 주요 원인이다. 예를 들어 어떤 CPU가 1사이클에 약 256 바이트를 처리할 수 있고, 메모리는 1사이클에 2바이트를 전송 가능하며, 해당 데이터가 메모리에서 CPU까지 도착하는데 10사이클 이상이 소요된다고 가정하자. 이 경우, CPU의 성능과 관계 없이 메모리로부터 적기에 데이터를 전송 받지 못해서 동작이 지연하는 현상이 발생할 것이다. | 캐시가 필요한 핵심적인 이유는, CPU 성능의 발전 속도와 DRAM 메모리 성능의 발전 속도의 차이이다. CPU 성능은 매년 약 55% 향상되지만, DRAM 메모리 성능은 매년 약 7% 향상된다. 이는 CPU와 메모리 사이의 병목 현상을 일으키는 주요 원인이다. 예를 들어 어떤 CPU가 1사이클에 약 256 바이트를 처리할 수 있고, 메모리는 1사이클에 2바이트를 전송 가능하며, 해당 데이터가 메모리에서 CPU까지 도착하는데 10사이클 이상이 소요된다고 가정하자. 이 경우, CPU의 성능과 관계 없이 메모리로부터 적기에 데이터를 전송 받지 못해서 동작이 지연하는 현상이 발생할 것이다. | ||
이때 핵심적인 관찰사항이 하나 존재한다. 이는 "CPU가 어떤 메모리 주소를 한번 접근했다면, 곧 같은 주소를 다시 접근할 가능성이 높다"라는 것이다. 이러한 성질을 temporal locality라고 하며, 이를 바탕으로 CPU가 자주 쓰는 데이터에 대해서 빠르게 접근할 수 있도록 개발된 것이 캐시이다. | 이때 핵심적인 관찰사항이 하나 존재한다. 이는 "'''CPU가 어떤 메모리 주소를 한번 접근했다면, 곧 같은 주소를 다시 접근할 가능성이 높다'''"라는 것이다. 이러한 성질을 temporal locality라고 하며, 이를 바탕으로 CPU가 자주 쓰는 데이터에 대해서 빠르게 접근할 수 있도록 개발된 것이 캐시이다. | ||
==Management of Cache== | ==Management of Cache== | ||
| 13번째 줄: | 13번째 줄: | ||
캐시는 하드웨어에 의해서 자동으로 관리된다. 즉, 캐시는 전적으로 CPU 설계에 따라 동작할 뿐, 어셈블리어등으로 조작될 수는 없다. 또한 캐시는 메모리와 비교했을 때, 그 크기는 작지만 CPU로부터의 접근 시간은 짧다. 따라서 공간이 작기 때문에 메인 메모리 데이터 전체가 아닌 일부만 저장 가능하며, 자주 접근하는 데이터만을 저장해야 한다. 이때 메인 메모리와 캐시 사이에서 데이터를 주고 받은 단위를 block이라고 하며, CPU 설계자가 block의 크기를 결정한다. | 캐시는 하드웨어에 의해서 자동으로 관리된다. 즉, 캐시는 전적으로 CPU 설계에 따라 동작할 뿐, 어셈블리어등으로 조작될 수는 없다. 또한 캐시는 메모리와 비교했을 때, 그 크기는 작지만 CPU로부터의 접근 시간은 짧다. 따라서 공간이 작기 때문에 메인 메모리 데이터 전체가 아닌 일부만 저장 가능하며, 자주 접근하는 데이터만을 저장해야 한다. 이때 메인 메모리와 캐시 사이에서 데이터를 주고 받은 단위를 block이라고 하며, CPU 설계자가 block의 크기를 결정한다. | ||
[[파일:Cache Miss.png|섬네일|210x210픽셀|Figure 2. Cache Miss ]] | [[파일:Cache Miss.png|섬네일|210x210픽셀|Figure 2. Cache Miss ]] | ||
Figure 1, 2는 각각 캐시 히트(hit)와 캐시 미스(miss)의 상황을 보여준다. 먼저 figure 1은 CPU가 블록 14번을 요청했는데 캐시에 이미 14번 블록이 존재하는 상황이다. 이를 캐시 | Figure 1, 2는 각각 캐시 히트(hit)와 캐시 미스(miss)의 상황을 보여준다. 먼저 figure 1은 CPU가 블록 14번을 '''요청했는데 캐시에 이미 14번 블록이 존재하는 상황이다. 이를 캐시 히트'''라고 하며, CPU는 캐시에서 바로 데이터를 읽어올 수 있고, 메인 메모리에 접근할 필요가 없어 속도가 빠르다. 반면, figure 2는 CPU가 '''블록 12번을 요청했는데 캐시에 12번 블록이 없는 상황이다. 이를 캐시 미스'''라고 하며, CPU는 메모리로부터 블록 12번을 가져와야 한다. 하지만 현재의 캐시 공간은 가득 차있기 때문에 기존의 블록 하나를 내보내야(evict) 한다. 이때 캐시 공간에 대한 replacement policy가 적용되고, 해당 예제에서는 블록 9번이 제거된다. 최종적으로 블록 12번이 캐시에 저장되고, 이것이 CPU에 전달된다. | ||
===Locality=== | ===Locality=== | ||
Locality란 프로그램이 실행되는 동안 같은 데이터나 인접한 데이터에 반복해서 접근하는 | '''Locality란 프로그램이 실행되는 동안 같은 데이터나 인접한 데이터에 반복해서 접근하는 경향'''이다. 캐시는 이 특성을 이용하여 성능을 향상시킨다. 먼저 '''temporal locality란 어떤 데이터가 한 번 참조되었다면, 곧 다시 해당 데이터가 참조될 가능성이 높다는 것'''이다. 또한 '''spatial locality란 어떤 데이터가 첨조되었다면, 그와 가까운 주소에 있는 데이터들도 곧 참조될 가능성이 높다는 것'''이다. 캐시는 이 두 가지 지역성을 활용해, 메인 메모리 접근을 줄이고 성능을 높인다. 아래는 locality 특성을 보여주는 예시 코드이다: | ||
<syntaxhighlight lang="c"> | <syntaxhighlight lang="c"> | ||
sum = 0; | sum = 0; | ||
| 28번째 줄: | 28번째 줄: | ||
==Multi-Level Cache== | ==Multi-Level Cache== | ||
[[파일:Typical Memory Hierarchy.png|섬네일|Figure 3. Typical Memory Hierarchy ]] | [[파일:Typical Memory Hierarchy.png|섬네일|Figure 3. Typical Memory Hierarchy ]] | ||
CPU는 보통 3단계 캐시 구조를 사용한다. 3단계 캐시 구조는 figure 3와 같이 L1, L2, L3 캐시로 이루어져 있다. 이는 3단계 캐시 구조: CPU는 보통 <code>L1 → L2 → L3 → Main Memory</code> 순서로 데이터를 찾는 동작 원리를 가진다. L1은 가장 빠르지만 용량이 적어지며, L2, L3로 갈수록 속도가 느려지더라도 그 용량이 커지는 경향을 보인다. 만약 L1, L2, L3 캐시에 모두 캐시 미스가 발생하면, CPU는 메인 메모리(DRAM)에 접근한다. | CPU는 보통 3단계 캐시 구조를 사용한다. 3단계 캐시 구조는 figure 3와 같이 L1, L2, L3 캐시로 이루어져 있다. 이는 3단계 캐시 구조: CPU는 보통 <code>'''L1 → L2 → L3 → Main Memory'''</code> 순서로 데이터를 찾는 동작 원리를 가진다. L1은 가장 빠르지만 용량이 적어지며, L2, L3로 갈수록 속도가 느려지더라도 그 용량이 커지는 경향을 보인다. 만약 L1, L2, L3 캐시에 모두 캐시 미스가 발생하면, CPU는 메인 메모리(DRAM)에 접근한다. | ||
이러한 구조를 가지고 있는 것은 속도가 빠를수록 비싸고 용량이 작아지고, 용량이 클수록 속도가 느려지고 | 이러한 구조를 가지고 있는 것은 '''속도가 빠를수록 비싸고 용량이 작아지고, 용량이 클수록 속도가 느려지고 싸진다'''는 메모리 하드웨어의 근본적인 특성 때문이다. 이러한 특성에 의해 메모리 계층 구조는 이는 하위 계층으로 갈수록 단순히 성능이 열등해지는 것이 아니라, 각 계층이 '''서로를 상호보완하는 구조'''를 가진다. 캐시 계층 구조에서, 일반적으로 레벨 k의 빠른 메모리는 레벨 k+1의 느린 메모리의 캐시 역할을 한다. 3단계 캐시 구조에서는 L1 캐시는 L2의 캐시, L2는 L3의 캐시와 같이 해당 개념이 적용된다.<ref>이때 캐시는 넓은 의미로 사용되어, 단순히 더 빠른 계층이라는 것을 의미한다</ref> | ||
Figure 3는 전형적인 메모리 계층 구조를 보여준다. L0는 CPU 내부의 레지스터를 의미하며, L1~L3는 캐시 계층이다. 또한 L4는 메인 메모리(DRAM), L5는 보조 기억 장치(SSD, 하드 디스크), L6는 클라우드 시스템과 같은 원격 저장소를 의미한다. 이때 캐시 계층 만이 가지는 주요한 특징은 어셈블리 수준의 프로그램에서도 캐시 계층을 직접 제어할 수 있다는 것이다. 레지스터와 DRAM은 프로그램이 명시적으로 조작 가능하지만, 캐시 계층을 하드웨어에 의해서 자동으로 관리되기 때문이다. | Figure 3는 전형적인 메모리 계층 구조를 보여준다. L0는 CPU 내부의 레지스터를 의미하며, L1~L3는 캐시 계층이다. 또한 L4는 메인 메모리(DRAM), L5는 보조 기억 장치(SSD, 하드 디스크), L6는 클라우드 시스템과 같은 원격 저장소를 의미한다. 이때 캐시 계층 만이 가지는 주요한 특징은 어셈블리 수준의 프로그램에서도 캐시 계층을 직접 제어할 수 있다는 것이다. 레지스터와 DRAM은 프로그램이 명시적으로 조작 가능하지만, 캐시 계층을 하드웨어에 의해서 자동으로 관리되기 때문이다. | ||
| 38번째 줄: | 38번째 줄: | ||
==Structure of cache memory== | ==Structure of cache memory== | ||
[[파일:Cache Memory Structure.png|섬네일|Figure 5. Cache Memory Structure ]] | [[파일:Cache Memory Structure.png|섬네일|Figure 5. Cache Memory Structure ]] | ||
캐시 메모리는 figure 5와 같이 조직되어 있다. 캐시 메모리는 S개의 | 캐시 메모리는 figure 5와 같이 조직되어 있다. '''캐시 메모리는 S개의 set'''로 구성되며, '''각 set에는 E개의 line(또는 block)'''이 존재한다. 그리고 각 line에는 다음과 같은 정보들이 저장된다: | ||
* valid bit (1비트): 이 line에 유효한 데이터가 있는지 여부 | * '''valid bit''' (1비트): 이 line에 유효한 데이터가 있는지 여부 | ||
* tag (t비트): 어떤 메모리 주소에서 왔는지를 구별하는 태그 | * '''tag''' (t비트): 어떤 메모리 주소에서 왔는지를 구별하는 태그 | ||
* data block (B바이트): 실제 데이터가 저장됨 | * '''data block''' (B바이트): 실제 데이터가 저장됨 | ||
따라서, 전체 캐시 크기는 데이터만 고려할 때 아래와 같다: | 따라서, 전체 캐시 크기는 데이터만 고려할 때 아래와 같다: | ||
Cache size = B × E × S (bytes) | '''Cache size = B × E × S (bytes)''' | ||
==Operation of Cache Memory== | |||
[[파일:Memory address structure.png|섬네일|Figure 6. Memory address structure]] | |||
캐시의 작동 원리를 이해하기 위해서는 먼저 메모리 주소가 어떻게 구성되는지에 대해서 이해해야 한다. 어떤 주소 x는 figure 6와 같이 세 부분으로 나뉜다: | |||
* tag 부분(t비트): 어떤 메모리 주소에서 왔는지를 구별하기 위해서 사용된다. | |||
** 같은 set 내에서도 다양한 주소에 해당하는 인스턴스값이 저장될 수 있으므로, tag를 이용해서 특정 주소값의 인스턴스가 저장되었는지 확인한다. | |||
* set index 부분(s비트): 주소가 주어졌을 때, 캐시 내의 어떤 set에 접근할지를 결정한다. | |||
* block offset 부분(b비트): 특정 set가 주어졌을 때, set 내의 블록에서 어느 위치의 바이트를 참조할지를 결정한다. | |||
이때, 주소가 총 m 바이트로 이루어져 있다면, 아래의 식이 성립한다. | |||
'''m = t + s + b''' | |||
또한, 정의에 따라 아래의 식들이 성립한다: | |||
* <code>M = 2<sup>m</sup></code>: 전체 메모리 공간 크기 | |||
* <code>B = 2<sup>b</sup></code>: 블록의 크기 | |||
* <code>S = 2<sup>s</sup></code>: 캐시 세트의 개수 | |||
* m: 메모리 주소의 길이(word size) | |||
* b, s, t: 각각 block offset, set, tag를 표현하기 위해 사용되는 비트의 수 | |||
[[파일:Memory address structure example.png|섬네일|300x300픽셀|Figure 7. Address structure example]] | |||
[[파일:Main memory structure.png|섬네일|Figure 8. Main memory structure]] | |||
[[파일:Operation of Cache Memory.png|섬네일|Figure 9. Operation of Cache Memory]] | |||
예를 들어, <code>M=65536(m=16), B=64(b=6), S=32(s=5)</code>일 때 프로그램이 0xAD8에 저장된 단일 바이트에 접근한다고 가정하자. 이 경우 주소 공간은 figure 7과 같이 구성된다. 또한 메모리 주소 공간은 figure 8과 같이 구성된다. Block offset이 0x18이라는 것은 해당 주소가 메모리 블록 내에서 0x18번째 바이트를 가리킨다는 뜻이다. 블록 사이즈가 <code>B=64</code>이므로, 각각의 블록은 64의 배수에서 시작한다. 따라서 주소 0xAD8은 0xAC0~0xAFF 사이에 존재하므로, 결과적으로 해당 주소가 해당 블록에서 가리키는 부분은 <code>0xAD8 - 0xAC0 = 0x18</code>이 되며, 이는 block offset과 일치한다.<br> | |||
또한, <code>set index = 0b01011</code>이다. 이 때문에 메인 메모리의 블록은 cache의 set #11에 블록 전체가 복사되어 들어간다.<br> | |||
또한, tag 부분인 0b00001도 함께 저장되며, cache가 나중에 같은 set에 접근했을 때 이 tag와 비교해 hit/miss를 판단하는데 사용된다. 추가적으로 valid bit도 1로 설정된다. 이러한 과정은 figure 9에 잘 나타나 있다. | |||
==[[Three Kinds of Cache Mapping]]== | |||
자세한 내용은 [[Three Kinds of Cache Mapping]] 문서를 참조해 주십시오. | |||
==Cache Performance== | |||
캐시의 퍼포먼스 측정은 임의의 주소를 바탕으로 데이터에 접근할 때 걸리는 시간을 바탕으로 이루어진다. 이를 위해 HT(hit time), MP(miss penalty)라는 개념이 도입된다. HT는 프로세서에 캐시 내에 존재하는 데이터를 전달하는데 걸리는 시간(사이클의 수)이다. 이는 캐시 내에 해당 데이터가 존재하는지 탐색하는 시간(사이클의 수)을 포함한다. MP는 캐시 미스에 의해서 추가적으로 소요되는 시간(사이클의 수)을 의미한다. 따라서, 캐시 히트일 때에는 HT만큼의 시간(사이클의 수)이 소요되고, 캐시 미스일 때에는 HT + MP만큼의 시간(사이클의 수)이 소요된다. 이를 통해서 캐시의 퍼포먼스를 측정하는데 가장 중요한 지표인 AMAT(Average Memory Access Time)을 구할 수 있다. 이는 임의의 주소를 바탕으로 데이터에 접근할 때 걸리는 평균적인 사이클의 수를 의미하며, 이는 아래와 같이 계산된다: | |||
AMAT = HT + miss_rate x MP | |||
먼저 계층적으로 이루어져 있지 않은 캐시(L1)에 대해 먼저 고려하자. 이 경우 CPU가 L1 캐시에서 데이터를 로드하는데는 1사이클이 소요되고, 메인 메모리에서 로드하는 데에는 1000 사이클이 소요된다고 가정하자. 또한 <code>hit rate = 80%</code>라고 가정하자. 이 경우, <code>AMAT = 1 + (1 - 0.8) x 1000 = 201</code>이다. | |||
[[파일:Multi-Level Cache.png|섬네일|200x200픽셀|Figure 8. Multi-Level Cache]] | |||
또한 Figure 8과 같이 계층적인 구조의 캐시를 고려하자. 이 경우 아래와 같은 조건이 주어졌다고 가정하자: | |||
* L1 캐시에서 데이터를 로드하는데 걸리는 사이클 수는 1, hit rate는 50% | |||
* L1 캐시에서 데이터를 로드하는데 걸리는 사이클 수는 10, hit rate는 75% | |||
* L1 캐시에서 데이터를 로드하는데 걸리는 사이클 수는 100, hit rate는 90% | |||
* 메인 메모리에서 데이터를 로드하는데 걸리는 사이클 수는 1000 | |||
이 경우 L1 캐시를 기준으로 하는 AMAT<sub>1</sub>은 아래와 같이 계산된다: | |||
AMAT<sub>1</sub> = 1 + (1 - 0.5) x (AMAT<sub>2</sub>) | |||
= 1 + (1−0.5) × (10 + (1−0.75) × (AMAT3)) | |||
= 1 + (1−0.5) × (10 + (1−0.75) × (100 + (1−0.9) × (AMATm))) | |||
= 1 + (1−0.5) × (10 + (1−0.75) × (100 + (1−0.9) × (1000))) | |||
= 1 + 0.5 × (10 + 0.25 × (100 + 100)) = 31 | |||
이와 같이 계층적인 캐시 구조를 사용할 때 AMAT이 크게 줄어드는 이유는, 메인 메모리에 접근할 확률이 크게 낮아졌기 때문이다. 이를 실제로 계산해보면, <code>0.5 × 0.25 × 0.1 = 0.0125 = 1.25%</code>이다. | |||
==Cache-Friendly Code== | |||
캐시의 성능을 최대한 활용하기 위해서는 locality를 최대한 활용해야 한다. 메모리에 접근할 때 spatial locality와 temporal locality를 최대한 활용하는 코드를 캐시 친화적인 코드라고 한다. 캐시는 메모리를 블록 단위로 메인 메모리에서 가져오므로, 연속된 메모리에 접근하도록 코드를 작성해야 한다. 먼저 아래와 같은 코드를 관찰하자: | |||
<syntaxhighlight lang="c"> | |||
for (i = 0; i < M; i++) | |||
for (j = 0; j < N; j++) | |||
sum += a[i][j]; | |||
</syntaxhighlight> | |||
해당 코드는 a[i][j]라는 2차원 배열에서 행을 먼저, 열을 나중에 접근하도록 설계되어 있다. 이때 C언어는 row-major order로 2차원 배열을 저장하므로, a[0][0], a[0][1], a[0][2], ... 이런 식으로 메모리에 저장한다. 따라서 해당 코드는 연속된 메모리 공간을 순차적으로 접근하므로 캐시 효율이 좋도록 설계되어 있다. | |||
<syntaxhighlight lang="c"> | |||
for (j = 0; j < N; j++) | |||
for (i = 0; i < M; i++) | |||
sum += a[i][j]; | |||
</syntaxhighlight> | |||
하지만 위의 코드는 a[i][j]에 대해 열을 먼저, 행을 나중에 접근한다. 메모리 상에는 불연속적으로 저장되어 있는 원소들을 반복적으로 접근하므로, 캐시 라인이 자주 업데이트되고 캐시 미스또한 자주 발생한다. | |||
==각주== | ==각주== | ||
2025년 6월 9일 (월) 11:48 기준 최신판
상위 문서: 컴퓨터 시스템
개요
캐시(Cache)는 기본적으로 음식, 무기, 보물 등을 저장하는 숨겨진 저장 공간이라는 뜻이다. 컴퓨터 시스템에서는 좁은 의미에서, CPU와 메인 메모리 사이에 위치한 중간 저장소를 의미하며, 최근에 사용된 데이터나 명령어를 저장한다. 이때 캐시는 메인 메모리보다 훨씬 작은 저장 공간을 가지지만, 메인 메모리보다 훨씬 빠르게 접근할 수 있어서 CPU와 메모리 사이의 병목 현상을 줄여준다. 캐시는 컴퓨터 공학 전반에서 더 넓은 의미로 사용되기도 하는데, 두 시스템 사이에서 데이터를 빠르게 전달하기 위한 어떤 중간 저장소도 포함한다. 이런 의미에서 사용되는 예시가 웹 캐시이다. 해당 문서에서는 좁은 의미에서의 캐시에 대해서 다룬다.
Necessity of Cache
캐시가 필요한 핵심적인 이유는, CPU 성능의 발전 속도와 DRAM 메모리 성능의 발전 속도의 차이이다. CPU 성능은 매년 약 55% 향상되지만, DRAM 메모리 성능은 매년 약 7% 향상된다. 이는 CPU와 메모리 사이의 병목 현상을 일으키는 주요 원인이다. 예를 들어 어떤 CPU가 1사이클에 약 256 바이트를 처리할 수 있고, 메모리는 1사이클에 2바이트를 전송 가능하며, 해당 데이터가 메모리에서 CPU까지 도착하는데 10사이클 이상이 소요된다고 가정하자. 이 경우, CPU의 성능과 관계 없이 메모리로부터 적기에 데이터를 전송 받지 못해서 동작이 지연하는 현상이 발생할 것이다.
이때 핵심적인 관찰사항이 하나 존재한다. 이는 "CPU가 어떤 메모리 주소를 한번 접근했다면, 곧 같은 주소를 다시 접근할 가능성이 높다"라는 것이다. 이러한 성질을 temporal locality라고 하며, 이를 바탕으로 CPU가 자주 쓰는 데이터에 대해서 빠르게 접근할 수 있도록 개발된 것이 캐시이다.
Management of Cache
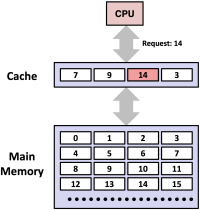
캐시는 하드웨어에 의해서 자동으로 관리된다. 즉, 캐시는 전적으로 CPU 설계에 따라 동작할 뿐, 어셈블리어등으로 조작될 수는 없다. 또한 캐시는 메모리와 비교했을 때, 그 크기는 작지만 CPU로부터의 접근 시간은 짧다. 따라서 공간이 작기 때문에 메인 메모리 데이터 전체가 아닌 일부만 저장 가능하며, 자주 접근하는 데이터만을 저장해야 한다. 이때 메인 메모리와 캐시 사이에서 데이터를 주고 받은 단위를 block이라고 하며, CPU 설계자가 block의 크기를 결정한다.
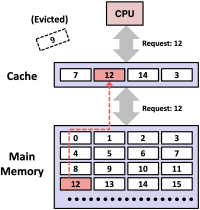
Figure 1, 2는 각각 캐시 히트(hit)와 캐시 미스(miss)의 상황을 보여준다. 먼저 figure 1은 CPU가 블록 14번을 요청했는데 캐시에 이미 14번 블록이 존재하는 상황이다. 이를 캐시 히트라고 하며, CPU는 캐시에서 바로 데이터를 읽어올 수 있고, 메인 메모리에 접근할 필요가 없어 속도가 빠르다. 반면, figure 2는 CPU가 블록 12번을 요청했는데 캐시에 12번 블록이 없는 상황이다. 이를 캐시 미스라고 하며, CPU는 메모리로부터 블록 12번을 가져와야 한다. 하지만 현재의 캐시 공간은 가득 차있기 때문에 기존의 블록 하나를 내보내야(evict) 한다. 이때 캐시 공간에 대한 replacement policy가 적용되고, 해당 예제에서는 블록 9번이 제거된다. 최종적으로 블록 12번이 캐시에 저장되고, 이것이 CPU에 전달된다.
Locality
Locality란 프로그램이 실행되는 동안 같은 데이터나 인접한 데이터에 반복해서 접근하는 경향이다. 캐시는 이 특성을 이용하여 성능을 향상시킨다. 먼저 temporal locality란 어떤 데이터가 한 번 참조되었다면, 곧 다시 해당 데이터가 참조될 가능성이 높다는 것이다. 또한 spatial locality란 어떤 데이터가 첨조되었다면, 그와 가까운 주소에 있는 데이터들도 곧 참조될 가능성이 높다는 것이다. 캐시는 이 두 가지 지역성을 활용해, 메인 메모리 접근을 줄이고 성능을 높인다. 아래는 locality 특성을 보여주는 예시 코드이다:
sum = 0;
for (i = 0; i < n; i++) {
sum += a[i];
}
return sum;
위 코드에서 변수 sum은 매 루프 반복마다 계속 사용되는데, 이는 변수의 temporal locality를 보여준다. 또한 배열 a[i]는 인접데이터에 따라 순차적으로 접근되므로, 이는 변수의 spatial locality를 보여준다. 사실 locality는 변수 혹은 데이터에만 적용되는 개념이 아니고, 코드에도 적용된다. 위 코드에서도 루프 안에 있는 add, cmp, jle 등의 명령어는 반복 실행되므로 temporal locality가 적용된다. 또한 위 코드의 명령어들은 메모리에 연속적으로 존재하며, 순서대로 실행되므로 역시 spatial locality가 적용될 수 있다.
Multi-Level Cache
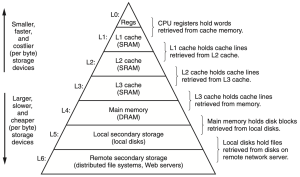
CPU는 보통 3단계 캐시 구조를 사용한다. 3단계 캐시 구조는 figure 3와 같이 L1, L2, L3 캐시로 이루어져 있다. 이는 3단계 캐시 구조: CPU는 보통 L1 → L2 → L3 → Main Memory 순서로 데이터를 찾는 동작 원리를 가진다. L1은 가장 빠르지만 용량이 적어지며, L2, L3로 갈수록 속도가 느려지더라도 그 용량이 커지는 경향을 보인다. 만약 L1, L2, L3 캐시에 모두 캐시 미스가 발생하면, CPU는 메인 메모리(DRAM)에 접근한다.
이러한 구조를 가지고 있는 것은 속도가 빠를수록 비싸고 용량이 작아지고, 용량이 클수록 속도가 느려지고 싸진다는 메모리 하드웨어의 근본적인 특성 때문이다. 이러한 특성에 의해 메모리 계층 구조는 이는 하위 계층으로 갈수록 단순히 성능이 열등해지는 것이 아니라, 각 계층이 서로를 상호보완하는 구조를 가진다. 캐시 계층 구조에서, 일반적으로 레벨 k의 빠른 메모리는 레벨 k+1의 느린 메모리의 캐시 역할을 한다. 3단계 캐시 구조에서는 L1 캐시는 L2의 캐시, L2는 L3의 캐시와 같이 해당 개념이 적용된다.[1]
Figure 3는 전형적인 메모리 계층 구조를 보여준다. L0는 CPU 내부의 레지스터를 의미하며, L1~L3는 캐시 계층이다. 또한 L4는 메인 메모리(DRAM), L5는 보조 기억 장치(SSD, 하드 디스크), L6는 클라우드 시스템과 같은 원격 저장소를 의미한다. 이때 캐시 계층 만이 가지는 주요한 특징은 어셈블리 수준의 프로그램에서도 캐시 계층을 직접 제어할 수 있다는 것이다. 레지스터와 DRAM은 프로그램이 명시적으로 조작 가능하지만, 캐시 계층을 하드웨어에 의해서 자동으로 관리되기 때문이다.

Figure 4는 CPU와 메모리 계층이 실제 컴퓨터 내에서 어떤 형태로 조직되어 있는지 보여준다. CPU 내부에는 ALU, 레지스터, 캐시 등이 포함되어 있다. 또한 I/O 브리지는 CPU와 메인 메모리, 입출력 장치 사시에서의 연결을 담당한다. 이때 버스 인터페이스가 CPU 내에 존재하여 CPU와 I/O 브리지 사이의 상호작용을 가능하게 한다.
Structure of cache memory
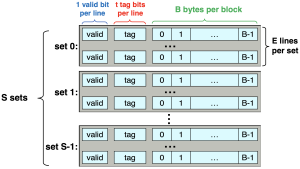
캐시 메모리는 figure 5와 같이 조직되어 있다. 캐시 메모리는 S개의 set로 구성되며, 각 set에는 E개의 line(또는 block)이 존재한다. 그리고 각 line에는 다음과 같은 정보들이 저장된다:
- valid bit (1비트): 이 line에 유효한 데이터가 있는지 여부
- tag (t비트): 어떤 메모리 주소에서 왔는지를 구별하는 태그
- data block (B바이트): 실제 데이터가 저장됨
따라서, 전체 캐시 크기는 데이터만 고려할 때 아래와 같다:
Cache size = B × E × S (bytes)
Operation of Cache Memory
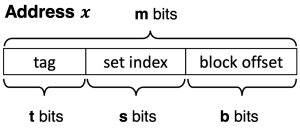
캐시의 작동 원리를 이해하기 위해서는 먼저 메모리 주소가 어떻게 구성되는지에 대해서 이해해야 한다. 어떤 주소 x는 figure 6와 같이 세 부분으로 나뉜다:
- tag 부분(t비트): 어떤 메모리 주소에서 왔는지를 구별하기 위해서 사용된다.
- 같은 set 내에서도 다양한 주소에 해당하는 인스턴스값이 저장될 수 있으므로, tag를 이용해서 특정 주소값의 인스턴스가 저장되었는지 확인한다.
- set index 부분(s비트): 주소가 주어졌을 때, 캐시 내의 어떤 set에 접근할지를 결정한다.
- block offset 부분(b비트): 특정 set가 주어졌을 때, set 내의 블록에서 어느 위치의 바이트를 참조할지를 결정한다.
이때, 주소가 총 m 바이트로 이루어져 있다면, 아래의 식이 성립한다.
m = t + s + b
또한, 정의에 따라 아래의 식들이 성립한다:
M = 2m: 전체 메모리 공간 크기B = 2b: 블록의 크기S = 2s: 캐시 세트의 개수- m: 메모리 주소의 길이(word size)
- b, s, t: 각각 block offset, set, tag를 표현하기 위해 사용되는 비트의 수

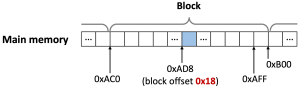
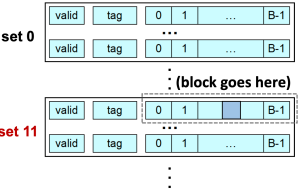
예를 들어, M=65536(m=16), B=64(b=6), S=32(s=5)일 때 프로그램이 0xAD8에 저장된 단일 바이트에 접근한다고 가정하자. 이 경우 주소 공간은 figure 7과 같이 구성된다. 또한 메모리 주소 공간은 figure 8과 같이 구성된다. Block offset이 0x18이라는 것은 해당 주소가 메모리 블록 내에서 0x18번째 바이트를 가리킨다는 뜻이다. 블록 사이즈가 B=64이므로, 각각의 블록은 64의 배수에서 시작한다. 따라서 주소 0xAD8은 0xAC0~0xAFF 사이에 존재하므로, 결과적으로 해당 주소가 해당 블록에서 가리키는 부분은 0xAD8 - 0xAC0 = 0x18이 되며, 이는 block offset과 일치한다.
또한, set index = 0b01011이다. 이 때문에 메인 메모리의 블록은 cache의 set #11에 블록 전체가 복사되어 들어간다.
또한, tag 부분인 0b00001도 함께 저장되며, cache가 나중에 같은 set에 접근했을 때 이 tag와 비교해 hit/miss를 판단하는데 사용된다. 추가적으로 valid bit도 1로 설정된다. 이러한 과정은 figure 9에 잘 나타나 있다.
Three Kinds of Cache Mapping
자세한 내용은 Three Kinds of Cache Mapping 문서를 참조해 주십시오.
Cache Performance
캐시의 퍼포먼스 측정은 임의의 주소를 바탕으로 데이터에 접근할 때 걸리는 시간을 바탕으로 이루어진다. 이를 위해 HT(hit time), MP(miss penalty)라는 개념이 도입된다. HT는 프로세서에 캐시 내에 존재하는 데이터를 전달하는데 걸리는 시간(사이클의 수)이다. 이는 캐시 내에 해당 데이터가 존재하는지 탐색하는 시간(사이클의 수)을 포함한다. MP는 캐시 미스에 의해서 추가적으로 소요되는 시간(사이클의 수)을 의미한다. 따라서, 캐시 히트일 때에는 HT만큼의 시간(사이클의 수)이 소요되고, 캐시 미스일 때에는 HT + MP만큼의 시간(사이클의 수)이 소요된다. 이를 통해서 캐시의 퍼포먼스를 측정하는데 가장 중요한 지표인 AMAT(Average Memory Access Time)을 구할 수 있다. 이는 임의의 주소를 바탕으로 데이터에 접근할 때 걸리는 평균적인 사이클의 수를 의미하며, 이는 아래와 같이 계산된다:
AMAT = HT + miss_rate x MP
먼저 계층적으로 이루어져 있지 않은 캐시(L1)에 대해 먼저 고려하자. 이 경우 CPU가 L1 캐시에서 데이터를 로드하는데는 1사이클이 소요되고, 메인 메모리에서 로드하는 데에는 1000 사이클이 소요된다고 가정하자. 또한 hit rate = 80%라고 가정하자. 이 경우, AMAT = 1 + (1 - 0.8) x 1000 = 201이다.
또한 Figure 8과 같이 계층적인 구조의 캐시를 고려하자. 이 경우 아래와 같은 조건이 주어졌다고 가정하자:
- L1 캐시에서 데이터를 로드하는데 걸리는 사이클 수는 1, hit rate는 50%
- L1 캐시에서 데이터를 로드하는데 걸리는 사이클 수는 10, hit rate는 75%
- L1 캐시에서 데이터를 로드하는데 걸리는 사이클 수는 100, hit rate는 90%
- 메인 메모리에서 데이터를 로드하는데 걸리는 사이클 수는 1000
이 경우 L1 캐시를 기준으로 하는 AMAT1은 아래와 같이 계산된다:
AMAT1 = 1 + (1 - 0.5) x (AMAT2)
= 1 + (1−0.5) × (10 + (1−0.75) × (AMAT3))
= 1 + (1−0.5) × (10 + (1−0.75) × (100 + (1−0.9) × (AMATm)))
= 1 + (1−0.5) × (10 + (1−0.75) × (100 + (1−0.9) × (1000)))
= 1 + 0.5 × (10 + 0.25 × (100 + 100)) = 31
이와 같이 계층적인 캐시 구조를 사용할 때 AMAT이 크게 줄어드는 이유는, 메인 메모리에 접근할 확률이 크게 낮아졌기 때문이다. 이를 실제로 계산해보면, 0.5 × 0.25 × 0.1 = 0.0125 = 1.25%이다.
Cache-Friendly Code
캐시의 성능을 최대한 활용하기 위해서는 locality를 최대한 활용해야 한다. 메모리에 접근할 때 spatial locality와 temporal locality를 최대한 활용하는 코드를 캐시 친화적인 코드라고 한다. 캐시는 메모리를 블록 단위로 메인 메모리에서 가져오므로, 연속된 메모리에 접근하도록 코드를 작성해야 한다. 먼저 아래와 같은 코드를 관찰하자:
for (i = 0; i < M; i++)
for (j = 0; j < N; j++)
sum += a[i][j];
해당 코드는 a[i][j]라는 2차원 배열에서 행을 먼저, 열을 나중에 접근하도록 설계되어 있다. 이때 C언어는 row-major order로 2차원 배열을 저장하므로, a[0][0], a[0][1], a[0][2], ... 이런 식으로 메모리에 저장한다. 따라서 해당 코드는 연속된 메모리 공간을 순차적으로 접근하므로 캐시 효율이 좋도록 설계되어 있다.
for (j = 0; j < N; j++)
for (i = 0; i < M; i++)
sum += a[i][j];
하지만 위의 코드는 a[i][j]에 대해 열을 먼저, 행을 나중에 접근한다. 메모리 상에는 불연속적으로 저장되어 있는 원소들을 반복적으로 접근하므로, 캐시 라인이 자주 업데이트되고 캐시 미스또한 자주 발생한다.
각주
- ↑ 이때 캐시는 넓은 의미로 사용되어, 단순히 더 빠른 계층이라는 것을 의미한다