Backtracking: 두 판 사이의 차이
| (같은 사용자의 중간 판 4개는 보이지 않습니다) | |||
| 83번째 줄: | 83번째 줄: | ||
==Constructing Subsets by Backtracking== | ==Constructing Subsets by Backtracking== | ||
해당 문단에서는 | 해당 문단에서는 주어진 집합의 모든 부분집합(2<sup>n</sup>개)을 백트래킹을 이용해서 생성하는 방법에 대해 설명한다. 즉, {1, 2, 3, …, n} 같은 집합이 있을 때 가능한 모든 조합(포함/비포함)을 탐색하는 문제에 대해서 다룬다. 이를 해결하기 위해서 각 원소 a[i]는 True/False 값을 가지는 크기가 n인 배열 a를 만들 수 있다. 이 경우 하나의 배열 a는 하나의 부분집합을 표현할 수 있다. 예를 들어, a = [True, False, True]는 부분집합 {1, 3}을 의미한다. 이를 백트래킹 표현으로 보면: | ||
# 각 단계 k마다 후보 집합 S<sub>k</sub> = (True,False) | # 각 단계 k마다 후보 집합 S<sub>k</sub> = (True,False) | ||
# 해가 완성되는 시점은 k가 n 이상, 즉 모든 원소에 대해 포함 여부를 결정했을 때이다. | # 해가 완성되는 시점은 k가 n 이상, 즉 모든 원소에 대해 포함 여부를 결정했을 때이다. | ||
| 180번째 줄: | 180번째 줄: | ||
위는 전체 프로그램을 실제로 실행시키는 함수이다. | 위는 전체 프로그램을 실제로 실행시키는 함수이다. | ||
==Applying Backtracking== | ==The Eight-Queens Problem== | ||
The Eight-Queens 문제는 8×8 체스판 위에 8개의 퀸(Queen)을 서로 공격하지 않도록 배치하는 문제이다. 즉, 한 퀸이 다른 퀸을 같은 행(row), 열(column), 대각선(diagonal) 에서 위협하지 않게 놓는 것이다. 이때 해당 문제의 목표는 가능한 모든 배치의 조합(해결 방법)을 찾는 것이다. | |||
이를 해결하기 위한 가장 핵심적인 아이디어는 "퀸들은 같은 행에 둘 수 없으므로, 각 행마다 정확히 한 퀸을 둔다."라는 것이다. 따라서 각 행(row) 에서 퀸이 놓이는 열(column) 위치만 저장하면 전체 배치를 표현할 수 있다. 예를 들어 a[i] = j라면, "i번째 행의 퀸이 j번째 열에 있다."라는 의미이다. 이때 중복없는 열의 위치만을 탐색하므로, 가능한 전체 조합은 <math>n!</math>이다. 따라서 <math>8!=40320</math>이므로 완전탐색으로도 빠르게 처리 가능하다. | |||
===Implementation of Eight Queens=== | |||
The Eight-Queens 문제를 구현하기 위한 핵심적인 알고리즘 구현 사항은 아래에 구현할 construct_candidates() 함수이다. 해당 함수는 k번째 행에 퀸을 둘 차례일 때, 이전에 놓인 퀸들과 열이나 대각선 충돌이 없는 위치만 후보로 추가한다: | |||
<syntaxhighlight lang="c"> | |||
void construct_candidates(int a[], int k, int n, int c[], int *ncandidates) { | |||
int i, j; | |||
bool legal_move; | |||
*ncandidates = 0; | |||
for (i = 1; i <= n; i++) { // i: 후보 column | |||
legal_move = true; | |||
for (j = 1; j < k; j++) { // 이미 놓인 퀸들과 비교 | |||
if (abs((k) - j) == abs(i - a[j])) // 대각선 충돌 검사 | |||
legal_move = false; | |||
if (i == a[j]) // 같은 열 충돌 검사 | |||
legal_move = false; | |||
} | |||
if (legal_move) { | |||
c[*ncandidates] = i; // 후보 저장 | |||
*ncandidates = *ncandidates + 1; | |||
} | |||
} | |||
} | |||
</syntaxhighlight> | |||
아래는 해결 루틴(backtrack) 안에서 사용하는 간단한 함수들이다. | |||
<syntaxhighlight lang="c"> | |||
int is_a_solution(int a[], int k, int n) { | |||
return (k == n); | |||
} | |||
</syntaxhighlight> | |||
위 함수는 현재 깊이 k가 전체 크기 n과 같으면 모든 행에 퀸을 놓은 완전한 해라는 것을 이용하여 해가 구해졌음을 알려준다. | |||
<syntaxhighlight lang="c"> | |||
void process_solution(int a[], int k, int input) { | |||
solution_count++; | |||
} | |||
</syntaxhighlight> | |||
완성된 해를 발견하면 해 수(solution_count) 증가를 시킨다. 아래는 전체 프로그램을 실행시키는 코드이다: | |||
<syntaxhighlight lang="c"> | |||
void nqueens(int n) { | |||
int a[NMAX]; /* solution vector */ | |||
solution_count = 0; | |||
backtrack(a, 0, n); | |||
printf("n=%d solution_count=%d\n", n, solution_count); | |||
} | |||
</syntaxhighlight> | |||
==Covering the Chess Board== | |||
Covering the Chess Board 문제는 체스의 주요 말 8개<ref>킹, 퀸, 룩x2, 비숍x2, 나이트x2</ref>를 체스판 위에 어떻게 놓아야 모든 64개의 칸이 적어도 한 말의 공격 범위에 들어가는지를 탐색하는 문제이다. 즉, 이는 Set Cover 문제의 한 종류라고 볼 수 있다. 사실 이 문제는 1849년부터 아무도 ‘모든 칸을 덮는 완전한 배치’를 찾지 못하였다. 하지만 해당 예시 문제를 살펴봄으로서 백트래킹 기법에 대한 이해를 높일 수 있을 것이다. | |||
이 문제의 핵심 개념은 조합 탐색(Combinatorial Search)으로, 가능한 모든 배치를 시도하면서 조건을 만족하는 해를 찾는 방식이다. 이때 이는 “현재 상태에서 유효하지 않으면 바로 되돌아감”과 같이 백트래킹으로 표현 가능하다. 이를 조합 탐색으로 해결하기 위해서는 8개의 말을 각각 64칸 중 하나에 배치해야 하므로: | |||
<math>\frac{64!}{(64-8)!}=64\times63\times62\times\cdots\times57\approx1.78\times10^{15}</math> | |||
즉, 약 10<sup>15</sup>가지 경우의 수를 살펴야 한다. 따라서 이렇게 많은 경우의 수를 컴퓨터가 탐색하는 것은 무리가 있으므로, 이를 컴퓨터가 전수 탐색(exhaustive search)하기는 비현실적이다. 이와 같이 가능한 조합의 수가 폭발적으로 많아지는 것을 “조합 폭발(Combinatorial Explosion)”이라고 한다. | |||
===Exploiting Symmetry=== | |||
컴퓨터가 모든 경우를 모두 탐색할 필요는 없다. 체스판은 좌우, 상하, 대각선 대칭, 회전 대칭<ref><math>90^\circ, 180^\circ, 270^\circ</math></ref>이 존재한다. 이때 서로 대칭적인 배치들은 사실상 동일한 결과를 내므로 중복 계산을 줄일 수 있다. 이를 적용함녀 탐색 공간이 약 <math>2.3\times 10^{12}</math>로, 약 천 배 줄어든다. 따라서 대칭성(symmetric equivalence)을 인식하면 탐색 공간을 급격히 줄일 수 있다는 점은 백트래킹 문제를 해결할 때 유용하게 써먹을 수 있는 포인트이다. | |||
===Pruning Branches=== | |||
또한 해당 문제를 풀 때에는 백트래킹의 핵심은 “불가능한 분기(branch)”를 일찍 자르는 pruning을 활용할 수 있다. 예를 들어 Queen은 최대 27칸을 위협할 수 있으며, Rook은 14칸, King은 8칸을 위협할 수 있다. 따라서 아직 덮지 못한 칸 수가, 나머지 말들이 덮을 수 있는 최대 범위의 합보다 많으면 해당 경우는 이미 불가능한 경우이므로 더 이상 탐색할 필요가 없다. 이러한 상한 기반 가지치기(bound pruning)로 탐색 공간의 95% 이상을 제거할 수 있다. | |||
===Conclusion=== | |||
대칭성을 활용하여 탐색 공간을 10<sup>12</sup>으로 줄였다고 해도, 초당 1000개의 경우의 수를 컴퓨터가 연산한다면, <math>10^{12}/10^3=10^9</math>초가 걸리는데, 이는 약 31.7년에 해당한다. 즉, 아직 충분히 빠르지는 않은 셈이다. 하지만 이에 대해 추가적인 가지치기 전략을 적용하고, 더 효율적인 탐색 순서를 사용하면 하루 미만의 계산으로 “해가 존재하지 않음”을 증명할 수 있다. 즉, 이 8개의 말로 모든 칸을 위협하는 배치는 존재하지 않는다. | |||
==Applying Backtracking(과제 문제)== | |||
===Bandwidth=== | ===Bandwidth=== | ||
대역폭(Bandwidth) 문제는 아래와 같은 입력과 목표를 가진다: | |||
입력: 그래프 <math>G=(V,E)</math><ref>정점 n개, 간선 m개</ref> | |||
목표: 주어진 모든 정점을 일렬로 배치했을 때<ref>정점 순열을 구한다.</ref>, 가장 긴 간선의 길이<ref>두 정점의 거리를 의미한다.</ref>를 최소화하는 순열을 찾는 것이다. | |||
[[파일:Figure 3. Bandwidth Problem.png|섬네일|Figure 3. Bandwidth Problem]] | |||
예를 들어 figure 3의 왼쪽 그림은 정점이 1~8 순서대로 있을 때 여러 간선이 길게 연결된 상태이고, 오른쪽 그림은 정점의 재배열을 통해서 간선의 길이가 더 짧아진 것을 보여준다. | |||
이 문제는 회로 설계(circuit layout), 행렬 재배열(linear algebra), 문서/메모리 최적화 등에 응용될 수 있다. 대역폭 문제는 NP-Complete 문제이기 때문에, 다항 시간에 정확히 푸는 알고리즘은 존재하지 않는다. 이를 해결하는 가장 단순한 방법은 가능한 모든 정점 순열 <math>n!</math>을 탐색하는 것이지만, 이는 <math>O(n!\times m)</math>의 시간 복잡도를 가지므로 매우 비효율적이다. 따라서 이를 해결하기 위해서는 완전 탐색이 아니라, 효율적인 백트래킹과 가지치기(pruning) 전략을 사용하여 근사적인 해를 구해야 한다. | |||
===Set Cover=== | |||
Set Cover 문제는 아래와 같은 입력과 목표를 가진다: | |||
입력: 원소들의 전체집합 <math>U=\{1,2,\cdots,n\}</math>과 여러 부분집합 <math>S_1,S_2,\cdots,S_m</math> | |||
목표: 이 부분집합들 중 일부를 골라서 <math>U</math> 전체를 덮되, 선택한 부분집합의 수가 최소가 되도록 한다. | |||
[[파일:Figure 4. Set Cover Problem.png|섬네일|210x210픽셀|Figure 4. Set Cover Problem]] | |||
즉, figure 4와 같이 입력이 주어졌을 때, <math>\bigcup_{i\in T}S_i=U</math>를 만족하는 최소 크기의 <math>T</math>를 찾는 문제이다. 이를 해결하는 가장 단순한 방법은 가능한 모든 부분집합을 확인하는 것이다. 하지만 가능한 부분집합의 개수는 <math>2^m</math>개이므로 시간복잡도가 <math>O(2^m\times n \times m)</math>이므로 매우 비효율적이다. 따라서 이를 해결하기 위해서는 완전 탐색이 아니라, 효율적인 백트래킹과 가지치기(pruning) 전략을 사용하여 근사적인 해를 구해야 한다. | |||
==각주== | ==각주== | ||
2025년 11월 18일 (화) 03:37 기준 최신판
상위 문서: 알고리즘 설계와 분석
개요
백트래킹은 탐색 공간(search space) 의 모든 가능한 구성을 체계적으로 탐색하는 방법dlek. 하지만 모든 문제에 똑같이 적용되는 알고리즘이 아니라, 각 문제에 맞게 커스터마이징해야 하는 일반적인 틀(general framework)이다. 이때 백트래킹은 결국 암묵적인 상태공간그래프(implicit state-space graph) 를 DFS 방식으로 탐색하는 것과 동일하며, 아래와 같은 특징을 가진다:
- Subsets/Permutations 탐색에 유용함: 백트래킹은 집합의 모든 부분집합이나 순열을 손쉽게 탐색할 수 있음.
- 정확성 보장: 가능한 모든 조합을 열거하므로, 누락 없이 정답을 찾을 수 있음.
- 효율성(Pruning): 단순 DFS보다 효율적으로 하기 위해 “불필요한 가지(dead branches)”를 잘라내야 함.
Sudoku and Backtracking
백트래킹(Backtracking)이란 모든 가능한 해(해답 공간, search space)를 탐색하면서 유망하지 않은 경로는 되돌아가는(recursive pruning)기법이다. 예를 들어 스도쿠를 해결하고자 할때 백트래킹 기법을 사용할 수 있다. 스도쿠는 모든 가능한 숫자 조합을 시도해야 하는 문제이기 때문에, 일종의 완전 탐색(exhaustive search)이 필요하다. 하지만 현실적으로 제약(Constraints) 을 이용하면 불가능한 경우를 일찍 걸러낼 수 있으며, 이러한 과정을 Pruning(가지치기)이라고 한다. 즉, 가능한 경우만 남기고 불가능한 경로는 조기 탈락시켜 효율을 높이는 것이다.
스도코의 문제의 해(각 칸, 혹은 각 열)를 벡터 a로 표기하고, 각 원소 ai는 해의 i번째 요소를 의미한다고 하자. 이때 각 ai는 가능한 선택지 집합인 유한 집합 Si 중 하나에서 선택된다. 이렇게 해를 벡터 형태로 구성하여 가능한 모든 조합을 탐색하는 것이 백트래킹 방식이다. 예를 들어 순열 문제에서는 ai는 i번째 위치에 올 숫자를 의미한다. 또한 부분집합 문제에서는 ai는 i번째 원소가 포함되어 있을 경우 true, 아니면 false로 설정된다.
스도쿠 문제를 백트래킹을 통해서 해결하고자 할때는 아래와 같은 절차를 따른다:
- 부분 해(partial solution)가 와 같이 존재한다.
- 해를 확장하기 위해서 가능한 후보 ak+1을 선택한다.
- 확장된 해가 유효한지(valid) 검사하여 만약 완전한 해이면 저장한다.
- 아니면, 아직 해가 될 가능성이 있다면 재귀(recursion)적으로 다음 단계를 진행한다.
- 가능성이 없다면 현재 선택을 “되돌리고(backtrack)” 다른 선택을 시도한다.
즉, “Try → Check → Recur → Undo and Try Next”를 재귀적으로 반복하여 문제를 해결하는 것이 백트래킹의 구조이다.
Backtracking Implementation
아래는 백트래킹의 핵심 알고리즘 구조를 보여주는 수도 코드이다:
Backtrack(a, k)
if a is a solution, print(a)
else {
k = k + 1
compute S_k
while S_k ≠ ∅ do
a_k = an element in S_k
S_k = S_k - a_k
Backtrack(a, k)
}
위 코드에서 각 변수는 아래와 같다:
- a: 현재까지 만들어진 부분해(partial solution) 벡터
- k: 현재 단계 (몇 번째 요소를 채우는 중인지)
- S_k: 현재 단계에서 가능한 후보(candidate) 집합
위 알고리즘은 아래와 같은 절차를 통해 작동한다:
- 기저 조건 검사: a가 완전한 해이면 출력(print(a))
- 아니라면 다음 단계로 확장
- k를 1 증가 (다음 위치로 이동)
- 가능한 후보 집합 S_k 계산
- 후보가 남아 있는 동안 반복:
- 하나를 선택해 a_k에 저장
- 그 후보를 제외하고 (S_k = S_k - a_k)
- 재귀적으로 Backtrack(a, k) 호출
위 절차를 통해서 모든 가능한 조합을 체계적으로 탐색하게 되었다.
Backtracking Implementation on C
아래는 백트래킹 기법을 C언어를 통해서 구현한 것이다:
void backtrack(int a[], int k, data input) {
int c[MAXCANDIDATES]; /* 후보 집합 */
int nc; /* 후보 수 */
int i; /* 반복용 변수 */
if (is_a_solution(a, k, input)) {
process_solution(a, k, input);
} else {
k = k + 1;
construct_candidates(a, k, input, c, &nc);
for (i = 0; i < nc; i++) {
a[k] = c[i];
make_move(a, k, input);
backtrack(a, k, input);
unmake_move(a, k, input);
if (finished) return; /* 조기 종료 조건 */
}
}
}
아래는 위에서 등장한 함수들에 대한 설명이다:
- is_a_solution(a, k, input): 현재까지 채운 해가 완전한 해(complete solution) 인지 판단하는 함수이다.
- construct_candidates(a, k, input, c, nc): 다음 단계에서 시도 가능한 후보들을 생성하는 함수이다.
- 현재까지 선택된 해 a[1..k-1]을 기반으로 k번째 위치에서 가능한 모든 선택지를 구한다.
- 후보들은 c 배열에 저장하며, 후보의 개수는 변수 nc에 저장한다.
- process_solution(a, k): 해를 출력하거나 카운트하거나 저장하는 등, 해를 처리하는 함수이다.
위 코드에서 is_a_solution, construct_candidates, process_solution 함수만 바꾸면 원하는 문제를 해결하기 위한 맞춤형 백트래킹 프로그램을 구현할 수 있다.
Constructing Subsets by Backtracking
해당 문단에서는 주어진 집합의 모든 부분집합(2n개)을 백트래킹을 이용해서 생성하는 방법에 대해 설명한다. 즉, {1, 2, 3, …, n} 같은 집합이 있을 때 가능한 모든 조합(포함/비포함)을 탐색하는 문제에 대해서 다룬다. 이를 해결하기 위해서 각 원소 a[i]는 True/False 값을 가지는 크기가 n인 배열 a를 만들 수 있다. 이 경우 하나의 배열 a는 하나의 부분집합을 표현할 수 있다. 예를 들어, a = [True, False, True]는 부분집합 {1, 3}을 의미한다. 이를 백트래킹 표현으로 보면:
- 각 단계 k마다 후보 집합 Sk = (True,False)
- 해가 완성되는 시점은 k가 n 이상, 즉 모든 원소에 대해 포함 여부를 결정했을 때이다.
결과적으로 가능한 조합 2n개가 모두 생선된다.
Subset Generation Tree / Order
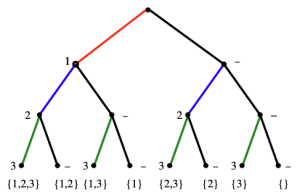
Figure 1은 부분집합을 생성하는 탐색 트리(Generation Tree)를 시각화한 것이다. 해당 트리는 루트에서 시작해서 각 단계마다 “포함한다”또는 “포함하지 않는다”의 두 가지 선택지를 가진다. 이때 트리의 깊이는 집합의 원소 개수 n과 같으며, leaf 노드는 완성된 부분집합을 의미한다.
이러한 원리를 백트래킹 코드에 대해 적용할 수 있다. 이를 위해 아래와 같은 조건을 이해하자:
- 길이가 n인 True/False 벡터를 통해 부분집합을 표현.
- 각 단계의 후보 집합 Sk=(True,False).
- 모든 원소를 처리했을 때 (k == n) → 완성된 해.
Implementation of Constructing Subsets
위에서 다룬 내용을 아래와 같이 기본적인 백트래킹 코드 틀(framework)안에 적용하여 C언어로 구현할 수 있다:
int is_a_solution(int a[], int k, int n) {
return (k == n);
}
위는 트리 깊이가 n단계가 되었는지를 확인하여 모든 원소를 처리했는가에 대해서 확인한다.
void construct_candidates(int a[], int k, int n, int c[], int *nc) {
c[0] = true;
c[1] = false;
*nc = 2;
}
각 단계마다 가능한 선택지는 항상 두 가지(True/False)이므로 이에 맞게 설정한다.
void process_solution(int a[], int k, int input) {
int i;
printf("{");
for (i = 1; i <= k; i++) {
if (a[i] == true) printf(" %d", i);
}
printf(" }\n");
}
위는 주어진 모든 부분 집합을 출력하는 코드이다. 이때 출력 대신 다른 검사를 수행하여 알고리즘의 기능을 확장할 수도 있다.
void generate_subsets(int n) {
int a[NMAX]; /* solution vector */
backtrack(a, 0, n);
}
위는 전체 프로그램을 실제로 실행시키는 함수이다.
Constructing Permutations by Backtracking
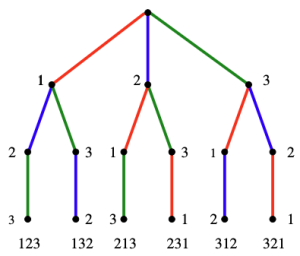
해당 문단에서는 백트래킹 기법을 이용하여 모든 순열을 생성하는 방법에 대해 설명한다. 순열(permutation)이란 n개의 원소를 서로 다른 순서로 배열하는 모든 경우의 수를 의미한다. 예를 들어, {1, 2, 3}의 순열은 123, 132, 213, 231, 312, 321이다. 이때 n개의 원소로 만들 수 있는 순열의 개수는 n!(팩토리얼)이다.
순열을 표현하기 위해서는 a라는 배열을 만들어야 하며, 이때 a[i]는 순열의 i번째 자리에 올 숫자를 나타낸다. 따라서 각 a[i]는 아직 사용되지 않은 숫자 중 하나를 선택해야 한다. 이를 백트래킹 알고리즘의 일반 형태로 표현하면:
즉, 아직 선택되지 않은 원소들의 집합이며, 이에 따라 완전한 해답은 k가 n 이상일 때 얻을 수 있다. Figure 2는 순열이 만들어지는 과정을 시각적으로 보여준다. 이는 루트 노드에서 시작하여, 가능한 후보들 중 하나를 선택하며 아래쪽으로 진행함에 따라 더욱 완전한 순열을 만들어 간다. 마지막 leaf 노드들은 완전한 순열들인 {123, 132, 213, 231, 312, 321}을 나타낸다.
Implementation of Constructing All Permutations
위에서 다룬 내용을 아래와 같이 기본적인 백트래킹 코드 틀(framework)안에 적용하여 C언어로 구현할 수 있다:
int is_a_solution(int a[], int k, int n) {
return (k == n);
}
위는 트리 깊이가 n단계가 되었는지를 확인하여 모든 원소를 처리했는가에 대해서 확인한다.
void construct_candidates(int a[], int k, int n, int c[], int *nc) {
int i;
bool in_perm[NMAX];
//현재 사용된 원소 표시 초기화
for (i = 1; i < NMAX; i++)
in_perm[i] = false;
//지금까지의 부분해 a[1..k-1]을 순회하며 이미 사용된 원소 표시
for (i = 1; i < k; i++)
in_perm[a[i]] = true;
//사용되지 않은 원소들만 후보 목록에 추가
*nc = 0;
for (i = 1; i <= n; i++) {
if (!in_perm[i]) {
c[*nc] = i;
*nc = *nc + 1;
}
}
}
위에서 in_perm[i]는 i가 현재 부분 순열에 포함되어 있는지를 나타내는 true/false 값이다. 또한 c[] 배열은 현재 단계에서 선택할 수 있는 후보(candidate) 리스트이다. 위 코드를 통해서 중복 없이 순열을 구성할 수 있다.
void generate_permutations(int n) {
int a[NMAX]; // 현재 부분해를 저장할 배열
backtrack(a, 0, n); // 백트래킹 호출
}
위는 전체 프로그램을 실제로 실행시키는 함수이다.
The Eight-Queens Problem
The Eight-Queens 문제는 8×8 체스판 위에 8개의 퀸(Queen)을 서로 공격하지 않도록 배치하는 문제이다. 즉, 한 퀸이 다른 퀸을 같은 행(row), 열(column), 대각선(diagonal) 에서 위협하지 않게 놓는 것이다. 이때 해당 문제의 목표는 가능한 모든 배치의 조합(해결 방법)을 찾는 것이다.
이를 해결하기 위한 가장 핵심적인 아이디어는 "퀸들은 같은 행에 둘 수 없으므로, 각 행마다 정확히 한 퀸을 둔다."라는 것이다. 따라서 각 행(row) 에서 퀸이 놓이는 열(column) 위치만 저장하면 전체 배치를 표현할 수 있다. 예를 들어 a[i] = j라면, "i번째 행의 퀸이 j번째 열에 있다."라는 의미이다. 이때 중복없는 열의 위치만을 탐색하므로, 가능한 전체 조합은 이다. 따라서 이므로 완전탐색으로도 빠르게 처리 가능하다.
Implementation of Eight Queens
The Eight-Queens 문제를 구현하기 위한 핵심적인 알고리즘 구현 사항은 아래에 구현할 construct_candidates() 함수이다. 해당 함수는 k번째 행에 퀸을 둘 차례일 때, 이전에 놓인 퀸들과 열이나 대각선 충돌이 없는 위치만 후보로 추가한다:
void construct_candidates(int a[], int k, int n, int c[], int *ncandidates) {
int i, j;
bool legal_move;
*ncandidates = 0;
for (i = 1; i <= n; i++) { // i: 후보 column
legal_move = true;
for (j = 1; j < k; j++) { // 이미 놓인 퀸들과 비교
if (abs((k) - j) == abs(i - a[j])) // 대각선 충돌 검사
legal_move = false;
if (i == a[j]) // 같은 열 충돌 검사
legal_move = false;
}
if (legal_move) {
c[*ncandidates] = i; // 후보 저장
*ncandidates = *ncandidates + 1;
}
}
}
아래는 해결 루틴(backtrack) 안에서 사용하는 간단한 함수들이다.
int is_a_solution(int a[], int k, int n) {
return (k == n);
}
위 함수는 현재 깊이 k가 전체 크기 n과 같으면 모든 행에 퀸을 놓은 완전한 해라는 것을 이용하여 해가 구해졌음을 알려준다.
void process_solution(int a[], int k, int input) {
solution_count++;
}
완성된 해를 발견하면 해 수(solution_count) 증가를 시킨다. 아래는 전체 프로그램을 실행시키는 코드이다:
void nqueens(int n) {
int a[NMAX]; /* solution vector */
solution_count = 0;
backtrack(a, 0, n);
printf("n=%d solution_count=%d\n", n, solution_count);
}
Covering the Chess Board
Covering the Chess Board 문제는 체스의 주요 말 8개[1]를 체스판 위에 어떻게 놓아야 모든 64개의 칸이 적어도 한 말의 공격 범위에 들어가는지를 탐색하는 문제이다. 즉, 이는 Set Cover 문제의 한 종류라고 볼 수 있다. 사실 이 문제는 1849년부터 아무도 ‘모든 칸을 덮는 완전한 배치’를 찾지 못하였다. 하지만 해당 예시 문제를 살펴봄으로서 백트래킹 기법에 대한 이해를 높일 수 있을 것이다.
이 문제의 핵심 개념은 조합 탐색(Combinatorial Search)으로, 가능한 모든 배치를 시도하면서 조건을 만족하는 해를 찾는 방식이다. 이때 이는 “현재 상태에서 유효하지 않으면 바로 되돌아감”과 같이 백트래킹으로 표현 가능하다. 이를 조합 탐색으로 해결하기 위해서는 8개의 말을 각각 64칸 중 하나에 배치해야 하므로:
즉, 약 1015가지 경우의 수를 살펴야 한다. 따라서 이렇게 많은 경우의 수를 컴퓨터가 탐색하는 것은 무리가 있으므로, 이를 컴퓨터가 전수 탐색(exhaustive search)하기는 비현실적이다. 이와 같이 가능한 조합의 수가 폭발적으로 많아지는 것을 “조합 폭발(Combinatorial Explosion)”이라고 한다.
Exploiting Symmetry
컴퓨터가 모든 경우를 모두 탐색할 필요는 없다. 체스판은 좌우, 상하, 대각선 대칭, 회전 대칭[2]이 존재한다. 이때 서로 대칭적인 배치들은 사실상 동일한 결과를 내므로 중복 계산을 줄일 수 있다. 이를 적용함녀 탐색 공간이 약 로, 약 천 배 줄어든다. 따라서 대칭성(symmetric equivalence)을 인식하면 탐색 공간을 급격히 줄일 수 있다는 점은 백트래킹 문제를 해결할 때 유용하게 써먹을 수 있는 포인트이다.
Pruning Branches
또한 해당 문제를 풀 때에는 백트래킹의 핵심은 “불가능한 분기(branch)”를 일찍 자르는 pruning을 활용할 수 있다. 예를 들어 Queen은 최대 27칸을 위협할 수 있으며, Rook은 14칸, King은 8칸을 위협할 수 있다. 따라서 아직 덮지 못한 칸 수가, 나머지 말들이 덮을 수 있는 최대 범위의 합보다 많으면 해당 경우는 이미 불가능한 경우이므로 더 이상 탐색할 필요가 없다. 이러한 상한 기반 가지치기(bound pruning)로 탐색 공간의 95% 이상을 제거할 수 있다.
Conclusion
대칭성을 활용하여 탐색 공간을 1012으로 줄였다고 해도, 초당 1000개의 경우의 수를 컴퓨터가 연산한다면, 초가 걸리는데, 이는 약 31.7년에 해당한다. 즉, 아직 충분히 빠르지는 않은 셈이다. 하지만 이에 대해 추가적인 가지치기 전략을 적용하고, 더 효율적인 탐색 순서를 사용하면 하루 미만의 계산으로 “해가 존재하지 않음”을 증명할 수 있다. 즉, 이 8개의 말로 모든 칸을 위협하는 배치는 존재하지 않는다.
Applying Backtracking(과제 문제)
Bandwidth
대역폭(Bandwidth) 문제는 아래와 같은 입력과 목표를 가진다:
입력: 그래프 [3] 목표: 주어진 모든 정점을 일렬로 배치했을 때[4], 가장 긴 간선의 길이[5]를 최소화하는 순열을 찾는 것이다.
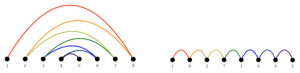
예를 들어 figure 3의 왼쪽 그림은 정점이 1~8 순서대로 있을 때 여러 간선이 길게 연결된 상태이고, 오른쪽 그림은 정점의 재배열을 통해서 간선의 길이가 더 짧아진 것을 보여준다.
이 문제는 회로 설계(circuit layout), 행렬 재배열(linear algebra), 문서/메모리 최적화 등에 응용될 수 있다. 대역폭 문제는 NP-Complete 문제이기 때문에, 다항 시간에 정확히 푸는 알고리즘은 존재하지 않는다. 이를 해결하는 가장 단순한 방법은 가능한 모든 정점 순열 을 탐색하는 것이지만, 이는 의 시간 복잡도를 가지므로 매우 비효율적이다. 따라서 이를 해결하기 위해서는 완전 탐색이 아니라, 효율적인 백트래킹과 가지치기(pruning) 전략을 사용하여 근사적인 해를 구해야 한다.
Set Cover
Set Cover 문제는 아래와 같은 입력과 목표를 가진다:
입력: 원소들의 전체집합 과 여러 부분집합 목표: 이 부분집합들 중 일부를 골라서 전체를 덮되, 선택한 부분집합의 수가 최소가 되도록 한다.
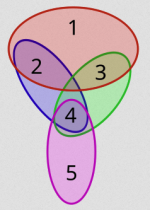
즉, figure 4와 같이 입력이 주어졌을 때, 를 만족하는 최소 크기의 를 찾는 문제이다. 이를 해결하는 가장 단순한 방법은 가능한 모든 부분집합을 확인하는 것이다. 하지만 가능한 부분집합의 개수는 개이므로 시간복잡도가 이므로 매우 비효율적이다. 따라서 이를 해결하기 위해서는 완전 탐색이 아니라, 효율적인 백트래킹과 가지치기(pruning) 전략을 사용하여 근사적인 해를 구해야 한다.