DFS: 두 판 사이의 차이
새 문서: 분류:알고리즘 설계와 분석 분류:컴퓨터 공학 상위 문서: 알고리즘 설계와 분석 ==개요== DFS(Depth-First Search) 알고리즘은 시작 정점에서 출발해서 한 방향으로 갈 수 있을 때까지 계속 이동하고, 더 이상 갈 곳이 없으면 바로 이전 단계로 되돌아(backtrack) 가서 다른 경로를 탐색하는 알고리즘이다. DFS 알고리즘의 핵심은 백트래킹(backtracking)이며, 모든 가능... |
|||
| (같은 사용자의 중간 판 15개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
[[분류:알고리즘 설계와 분석]] | [[분류:알고리즘 설계와 분석]] | ||
[[분류:컴퓨터 공학]] | [[분류:컴퓨터 공학]] | ||
상위 문서: [[Graph| | 상위 문서: [[Graph#Graph Traversal|Graph]] | ||
==개요== | ==개요== | ||
| 44번째 줄: | 44번째 줄: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
===Finding Paths=== | |||
DFS는 정점을 처음 발견했을 때 “누가 이 정점을 발견했는지”를 parent[] 배열에 기록한다: | |||
* parent[i] = 정점 i를 처음 큐에 넣게 만든 “직전의” 정점(발견자). | |||
** 시작 정점 s는 보통 parent[s] = -1로 표시함. | |||
* 모든 parent 화살표를 모으면, 시작 정점을 루트 노드로 하는 “발견 트리(discovery tree)”가 생김 | |||
** 이 트리는 탐색 순서를 보존함. 즉, 어떤 정점이 어떤 정점을 통해 처음 도달되었는지를 담고 있어, 경로 복원 등에 사용됨. | |||
아래는 parent[]를 이용해 끝점에서 시작점으로 거꾸로 따라가면 경로를 복원하는 함수이다: | |||
<syntaxhighlight lang="c"> | |||
void find_path(int start, int end, int parents[]) { | |||
if ((start == end) || (end == -1)) { //루트 노드에 도달 | |||
printf("\n%d", start); | |||
} else { | |||
find_path(start, parents[end], parents); //end의 부모 쪽으로 한 칸 올라가서 해당 경로 출력 | |||
printf(" %d", end); | |||
} | |||
} | |||
</syntaxhighlight> | |||
==DFS with Graph== | |||
[[파일:Figure 1. Graph to DFS tree.png|섬네일|Figure 1. Graph to DFS tree]] | |||
DFS 알고리즘은 탐색하는 그래프의 간선들의 구조를 조직화한다. DFS를 수행하면 그래프의 모든 간선이 “방문 순서”에 따라 방향성을 가진다. 즉, undirected 그래프를 탐색하더라도 “어떤 정점이 다른 정점을 처음 발견했는가”에 따라 간선의 방향이 결정된다. Figure 1은 원래의 undirected 그래프로부터 DFS 알고리즘을 수행하여 DFS 트리 자료구조를 만드는 것을 보여준다. | |||
===Edge Classification for DFS=== | |||
[[파일:Figure 2. Edge Classification for DFS.png|섬네일|Figure 2. Edge Classification for DFS]] | |||
DFS 알고리즘을 실행하여 어떤 그래프를 탐색하는 과정에서 탐색하는 그래프의 간선들은 아래와 같이 4가지로 분류된다: | |||
# Tree Edge: DFS 트리에서 새 정점을 발견하는 간선(해당 간선의 집합은 DFS 트리를 구성) | |||
# Forward Edge: 이미 방문한 정점으로 향하지만, 자신의 “자손”인 경우 | |||
# Back Edge: 자신의 “조상”으로 되돌아가는 간선.(사이클이 존재함을 의미) | |||
# Cross Edge: DFS 트리의 서로 다른 가지(branch) 사이를 연결하는 간선 | |||
이와 같은 구분은 figure 2가 잘 보여준다. 아래는 DFS 실행 중 각 간선을 만날 때 호출되어, 간선의 성격을 자동으로 분류하는 함수이다: | |||
<syntaxhighlight lang="c"> | <syntaxhighlight lang="c"> | ||
int edge_classification(int x, int y) { | |||
if (parent[y] == x) return TREE; | |||
if (discovered[y] && !processed[y]) return BACK; | |||
if (processed[y] && entry_time[y] > entry_time[x]) return FORWARD; | |||
if (processed[y] && entry_time[y] < entry_time[x]) return CROSS; | |||
printf("Warning: self loop (%d,%d)\n", x, y); | |||
return -1; | |||
} | |||
</syntaxhighlight> | |||
이때 DFS가 undirected 그래프를 탐색하는 경우, forward/cross edges는 존재하지 않는다. | |||
==Analyzing Graph with DFS== | |||
DFS는 단순히 “모든 노드를 탐색하는 알고리즘”에 그치지 않고, 그래프의 구조적 특성을 분석하는 도구로서 매우 강력하게 활용된다. 특히 Cycle Detection 문제와 Articulation Vertices 문제를 해결하는데에 자주 사용된다: | |||
* Cycle Detection: 그래프에 cycle이 존재하는가를 판별. | |||
* Articulation Vertices: 어떤 노드를 제거하면 그래프가 별개의 그래프들로 구분되는지. | |||
===Finding Cycles=== | |||
DFS 알고리즘을 통해서 사이클을 찾는 방법은 DFS 중 발견되는 “Back Edge”를 활용하는 것이다. 이는 아래와 같은 과정을 필요로 한다: | |||
# DFS 알고리즘에 따라 어떤 정점 x를 방문한다. | |||
# 어떤 정점 x에서 아직 탐색이 완전히 끝나지 않은<ref>processed[x] == false인 상태를 의미한다.</ref> 조상 정점 y로 향하는 간선을 만나면, 해당 간선은 back edge에 해당한다. | |||
# Back edge의 존재는 cycle이 존재한다는 것을 의미한다. | |||
아래는 이를 구현하는 C언어 코드이다: | |||
<syntaxhighlight lang="c"> | |||
void process_edge(int x, int y) { | |||
if (parent[y] != x) { /* found back edge! */ | |||
printf("Cycle from %d to %d:", y, x); | |||
find_path(y, x, parent); | |||
finished = true; | |||
} | |||
} | |||
</syntaxhighlight> | </syntaxhighlight> | ||
< | 위 코드에서 y가 x의 부모 노드가 아니라면 이는 back edge이므로<ref>이때 x와 y 사이의 간선이 처리되지 않았으므로 당연히 processed[y] == false이다.</ref> 이에 따라 사이클이 발견되었음을 출력한다. 또한 find_path() 함수가 활용되었는데, 이는 DFS 트리 상에서 y에서 x로 이어지는 경로를 따라가며 출력하는 역할을 한다. 그리고 cycle을 이미 찾았으므로, finished 변수를 true로 만들어 탐색을 종료한다. | ||
===Articulation Vertices=== | |||
[[파일:Figure 3. Articulation Vertices.png|섬네일|Figure 3. Articulation Vertices]] | |||
Articulation Vertices 문제는 “어떤 노드를 제거하면 그래프가 분리되는가?”를 찾는 문제이다. 단절점(Articulation Vertex)란 특정 정점을 삭제했을 때 그래프가 둘 이상으로 분리되는 정점을 의미한다. Figure 3에서는 빨간색 정점이 단절점이며, 그 정점을 지우면 그래프가 왼쪽(파란 부분)과 오른쪽(초록 부분)으로 분리된다. 단절점 문제를 해결하는 가장 단순한 방법은 모든 정점에 대해 다음을 반복하는 것이다: | |||
# 해당 정점을 제거한다. | |||
# 남은 그래프에 DFS 또는 BFS를 수행한다. | |||
# 그래프가 여전히 연결되어 있는지 확인한다. | |||
위 알고리즘의 시간 복잡도는 정점의 개수가 n, 간선의 개수가 m일 때 정점을 하나 제거할 때마다 DFS를 한번 수행하므로 O(n × (m + n))이다. 이는 느리지만 개념적으로 articulation vertex의 정의를 충실히 따르는 방법이다. | |||
하지만, 이보다 더욱 빠르게 단절점을 탐색하는 알고리즘이 존재한다. 이 알고리즘은 Tarjan’s Algorithm으로, 한 번의 DFS 탐색 중에 단절점을 판별하는 방식이다. 이에 따라 O(n + m)의 시간복잡도를 가진다. Tarjan’s Algorithm의 핵심아이디어는 DFS 트리에서, 어떤 정점 v가 다음 조건을 만족하면 단절점이라는 것이다: | |||
# v는 루트가 아닌 정점이고, | |||
# v의 모든 서브 트리가 v의 조상(ancestor)으로 연결되는 Back Edge를 가지지 않아야 한다. | |||
[[파일:Figure 4. A Faster DFS Algorithm.png|섬네일|200x200픽셀|Figure 4. A Faster DFS Algorithm]] | |||
Figure 4는 특정 노드 v의 서브트리가 얼마나 v에 의존하는지, 그리고 그로 인해 어떤 노드들이 단절점(articulation point) 이 되는지를 시각적으로 보여주는 그림이다. 즉, v 또는 특정 조상 노드를 제거했을 때 그래프가 어떻게 분리되는지를 나타낸 예시이다. | |||
# root cutnode(빨간색): DFS 트리의 루트가 여러 개의 독립된 서브트리를 가지고 있다면, 루트를 제거하는 순간 이 서브트리들이 서로 완전히 분리된다. 따라서 루트 역시 단절점이 될 수 있음을 보여준다. | |||
# bridge cutnode(파란색): 파란 노드 아래에 있는 서브트리는 다른 조상 노드로 이어지는 back-edge가 전혀 없다. 즉, 이 서브트리는 해당 노드에 100% 의존해서만 그래프의 나머지 부분과 연결된다. 이런 경우 그 노드는 bridge(단절 간선)의 한쪽 끝점이며, 그 자체도 단절점이 된다. | |||
# parent cutnode(초록색): 특정 노드 v의 부모 노드가, v의 서브트리가 갖는 low-link 값 때문에 단절점 조건을 만족할 수 있음을 보여주는 예시다. 즉, 부모를 제거하면 v와 그 하위 서브트리 전체가 고립되므로 부모도 articulation point가 된다. | |||
이처럼 Figure 4는 v를 포함한 여러 서브트리가 어떻게 특정 노드에 구조적으로 의존하는지를 나타내며, 그 결과 어떤 노드들이 단절점이 되는지를 이해하기 쉽게 보여주는 그림이다. | |||
==Applications of DFS== | |||
===[[Topological Sorting]]=== | |||
자세한 내용은 [[Topological Sorting]] 문서를 참조하여 주십시오. | |||
</ | ===Strongly Connected Components=== | ||
어떤 방향 그래프(directed graph) 가 strongly connected하다는 것은 모든 정점 쌍 (u, v)에 대해, u → v 경로와 v → u 경로가 모두 존재한다는 뜻이다. 이때 어떤 그래프의 SCC(Strongly Connected Component)란 그래프에 존재하는 strongly connected된 각 그룹들을 의미한다. 이때 SCC는 더 이상 합칠 수 없는 최대 단위로, Maximal subset이라고 볼 수 있다. 이에 따라 그래프의 모든 정점은 정확히 하나의 SCC에만 속하며, SCC들은 그래프의 정점을 서로 겹치지 않게 분할(partition) 한다. | |||
[[파일:Figure 5. Finding SCC with DFS.png|섬네일|300x300픽셀|Figure 5. Finding SCC with DFS]] | |||
가장 널리 쓰이는 SCC를 찾는 알고리즘은 DFS 기반의 Kosaraju’s Algorithm이다. 이는 figure 5에 그 양상이 나타나 있다. Kosaraju’s Algorithm은 아래와 같은 과정을 통해서 SCC를 찾는다.: | |||
# 1차 DFS on G: G에 대해 DFS를 수행하고, 각 정점의 완료 순서를 스택에 저장. | |||
# Transpose Graph G<sup>t</sup> 생성: 모든 간선의 방향을 뒤집는다. | |||
# 2차 DFS on G<sup>t</sup>: 스택의 “가장 나중에 완료된 정점”<ref>Figure를 기준으로는 1번 정점에 해당한다. 8번 정점은 가장 나중에 완료되었다.</ref>부터 DFS 시작. | |||
마지막 단계를 거친 후, 각 DFS 탐색이 하나의 SCC가 된다. 따라서 해당 알고리즘의 시간 복잡도는 O(V + E)(정점 + 간선 수에 선형 비례)이므로 매우 효율적이다. | |||
==각주== | ==각주== | ||
2025년 11월 17일 (월) 11:56 기준 최신판
상위 문서: Graph
개요
DFS(Depth-First Search) 알고리즘은 시작 정점에서 출발해서 한 방향으로 갈 수 있을 때까지 계속 이동하고, 더 이상 갈 곳이 없으면 바로 이전 단계로 되돌아(backtrack) 가서 다른 경로를 탐색하는 알고리즘이다. DFS 알고리즘의 핵심은 백트래킹(backtracking)이며, 모든 가능한 경로를 포괄적으로 탐색(exhaustive search)할 수 있다.
DFS Code
Data Structures for BFS
BFS를 구현하기 위해 필요한 자료구조는 3가지이다:
bool processed[MAXV+1]; // 이미 완전히 처리된 정점
bool discovered[MAXV+1]; // 발견되었지만 방문되지 않은 정점
int parent[MAXV+1]; // 해당 정점을 방문하기 전의 부모 노드
processed[] 배열은 어떤 정점 v의 모든 인접 노드들이 모두 발견되었을때 true로 설정된다. 즉, 이 노드로부터 나가는 간선들은 모두 처리 완료됐다는 의미이다. BFS에서 processed[] 배열은 중복된 간선 처리나 사이클 검출을 막는 역할을 한다.
Implementing DFS
DFS 알고리즘은 보통 재귀적으로 구현된다. 이에 따라 스택 자료구조를 명시적으로 사용할 필요가 없는데, 재귀 호출이 스택과 같이 동작하기 때문이다. 아래는 DFS 알고리즘을 구현하는 C언어 코드이다:
void dfs(graph *g, int v) {
if (finished) return; // 탐색 종료 조건 (예: 특정 목표를 찾은 경우)
discovered[v] = true; // v를 처음 방문
process_vertex_early(v); // v 방문 직후 처리
p = g->edges[v]; // v의 인접 리스트 시작점
while (p != NULL) {
y = p->y; // v와 연결된 정점 y
if (!discovered[y]) { // 아직 방문하지 않았다면
parent[y] = v; // 부모 설정
process_edge(v,y);// 간선 처리
dfs(g, y); // 재귀 호출 (깊이 탐색)
} else if ((...조건...)) {
process_edge(v,y);// 이미 방문된 노드일 경우 (역방향 등)
}
if (finished) return; // 조기 종료
p = p->next; // 다음 간선으로
}
process_vertex_late(v); // v에서 더 이상 갈 곳이 없을 때 처리
processed[v] = true; // 완전히 처리 완료
}
Finding Paths
DFS는 정점을 처음 발견했을 때 “누가 이 정점을 발견했는지”를 parent[] 배열에 기록한다:
- parent[i] = 정점 i를 처음 큐에 넣게 만든 “직전의” 정점(발견자).
- 시작 정점 s는 보통 parent[s] = -1로 표시함.
- 모든 parent 화살표를 모으면, 시작 정점을 루트 노드로 하는 “발견 트리(discovery tree)”가 생김
- 이 트리는 탐색 순서를 보존함. 즉, 어떤 정점이 어떤 정점을 통해 처음 도달되었는지를 담고 있어, 경로 복원 등에 사용됨.
아래는 parent[]를 이용해 끝점에서 시작점으로 거꾸로 따라가면 경로를 복원하는 함수이다:
void find_path(int start, int end, int parents[]) {
if ((start == end) || (end == -1)) { //루트 노드에 도달
printf("\n%d", start);
} else {
find_path(start, parents[end], parents); //end의 부모 쪽으로 한 칸 올라가서 해당 경로 출력
printf(" %d", end);
}
}
DFS with Graph

DFS 알고리즘은 탐색하는 그래프의 간선들의 구조를 조직화한다. DFS를 수행하면 그래프의 모든 간선이 “방문 순서”에 따라 방향성을 가진다. 즉, undirected 그래프를 탐색하더라도 “어떤 정점이 다른 정점을 처음 발견했는가”에 따라 간선의 방향이 결정된다. Figure 1은 원래의 undirected 그래프로부터 DFS 알고리즘을 수행하여 DFS 트리 자료구조를 만드는 것을 보여준다.
Edge Classification for DFS
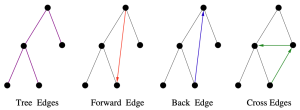
DFS 알고리즘을 실행하여 어떤 그래프를 탐색하는 과정에서 탐색하는 그래프의 간선들은 아래와 같이 4가지로 분류된다:
- Tree Edge: DFS 트리에서 새 정점을 발견하는 간선(해당 간선의 집합은 DFS 트리를 구성)
- Forward Edge: 이미 방문한 정점으로 향하지만, 자신의 “자손”인 경우
- Back Edge: 자신의 “조상”으로 되돌아가는 간선.(사이클이 존재함을 의미)
- Cross Edge: DFS 트리의 서로 다른 가지(branch) 사이를 연결하는 간선
이와 같은 구분은 figure 2가 잘 보여준다. 아래는 DFS 실행 중 각 간선을 만날 때 호출되어, 간선의 성격을 자동으로 분류하는 함수이다:
int edge_classification(int x, int y) {
if (parent[y] == x) return TREE;
if (discovered[y] && !processed[y]) return BACK;
if (processed[y] && entry_time[y] > entry_time[x]) return FORWARD;
if (processed[y] && entry_time[y] < entry_time[x]) return CROSS;
printf("Warning: self loop (%d,%d)\n", x, y);
return -1;
}
이때 DFS가 undirected 그래프를 탐색하는 경우, forward/cross edges는 존재하지 않는다.
Analyzing Graph with DFS
DFS는 단순히 “모든 노드를 탐색하는 알고리즘”에 그치지 않고, 그래프의 구조적 특성을 분석하는 도구로서 매우 강력하게 활용된다. 특히 Cycle Detection 문제와 Articulation Vertices 문제를 해결하는데에 자주 사용된다:
- Cycle Detection: 그래프에 cycle이 존재하는가를 판별.
- Articulation Vertices: 어떤 노드를 제거하면 그래프가 별개의 그래프들로 구분되는지.
Finding Cycles
DFS 알고리즘을 통해서 사이클을 찾는 방법은 DFS 중 발견되는 “Back Edge”를 활용하는 것이다. 이는 아래와 같은 과정을 필요로 한다:
- DFS 알고리즘에 따라 어떤 정점 x를 방문한다.
- 어떤 정점 x에서 아직 탐색이 완전히 끝나지 않은[1] 조상 정점 y로 향하는 간선을 만나면, 해당 간선은 back edge에 해당한다.
- Back edge의 존재는 cycle이 존재한다는 것을 의미한다.
아래는 이를 구현하는 C언어 코드이다:
void process_edge(int x, int y) {
if (parent[y] != x) { /* found back edge! */
printf("Cycle from %d to %d:", y, x);
find_path(y, x, parent);
finished = true;
}
}
위 코드에서 y가 x의 부모 노드가 아니라면 이는 back edge이므로[2] 이에 따라 사이클이 발견되었음을 출력한다. 또한 find_path() 함수가 활용되었는데, 이는 DFS 트리 상에서 y에서 x로 이어지는 경로를 따라가며 출력하는 역할을 한다. 그리고 cycle을 이미 찾았으므로, finished 변수를 true로 만들어 탐색을 종료한다.
Articulation Vertices
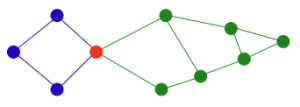
Articulation Vertices 문제는 “어떤 노드를 제거하면 그래프가 분리되는가?”를 찾는 문제이다. 단절점(Articulation Vertex)란 특정 정점을 삭제했을 때 그래프가 둘 이상으로 분리되는 정점을 의미한다. Figure 3에서는 빨간색 정점이 단절점이며, 그 정점을 지우면 그래프가 왼쪽(파란 부분)과 오른쪽(초록 부분)으로 분리된다. 단절점 문제를 해결하는 가장 단순한 방법은 모든 정점에 대해 다음을 반복하는 것이다:
- 해당 정점을 제거한다.
- 남은 그래프에 DFS 또는 BFS를 수행한다.
- 그래프가 여전히 연결되어 있는지 확인한다.
위 알고리즘의 시간 복잡도는 정점의 개수가 n, 간선의 개수가 m일 때 정점을 하나 제거할 때마다 DFS를 한번 수행하므로 O(n × (m + n))이다. 이는 느리지만 개념적으로 articulation vertex의 정의를 충실히 따르는 방법이다.
하지만, 이보다 더욱 빠르게 단절점을 탐색하는 알고리즘이 존재한다. 이 알고리즘은 Tarjan’s Algorithm으로, 한 번의 DFS 탐색 중에 단절점을 판별하는 방식이다. 이에 따라 O(n + m)의 시간복잡도를 가진다. Tarjan’s Algorithm의 핵심아이디어는 DFS 트리에서, 어떤 정점 v가 다음 조건을 만족하면 단절점이라는 것이다:
- v는 루트가 아닌 정점이고,
- v의 모든 서브 트리가 v의 조상(ancestor)으로 연결되는 Back Edge를 가지지 않아야 한다.
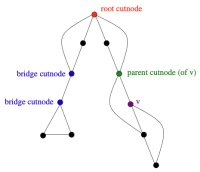
Figure 4는 특정 노드 v의 서브트리가 얼마나 v에 의존하는지, 그리고 그로 인해 어떤 노드들이 단절점(articulation point) 이 되는지를 시각적으로 보여주는 그림이다. 즉, v 또는 특정 조상 노드를 제거했을 때 그래프가 어떻게 분리되는지를 나타낸 예시이다.
- root cutnode(빨간색): DFS 트리의 루트가 여러 개의 독립된 서브트리를 가지고 있다면, 루트를 제거하는 순간 이 서브트리들이 서로 완전히 분리된다. 따라서 루트 역시 단절점이 될 수 있음을 보여준다.
- bridge cutnode(파란색): 파란 노드 아래에 있는 서브트리는 다른 조상 노드로 이어지는 back-edge가 전혀 없다. 즉, 이 서브트리는 해당 노드에 100% 의존해서만 그래프의 나머지 부분과 연결된다. 이런 경우 그 노드는 bridge(단절 간선)의 한쪽 끝점이며, 그 자체도 단절점이 된다.
- parent cutnode(초록색): 특정 노드 v의 부모 노드가, v의 서브트리가 갖는 low-link 값 때문에 단절점 조건을 만족할 수 있음을 보여주는 예시다. 즉, 부모를 제거하면 v와 그 하위 서브트리 전체가 고립되므로 부모도 articulation point가 된다.
이처럼 Figure 4는 v를 포함한 여러 서브트리가 어떻게 특정 노드에 구조적으로 의존하는지를 나타내며, 그 결과 어떤 노드들이 단절점이 되는지를 이해하기 쉽게 보여주는 그림이다.
Applications of DFS
Topological Sorting
자세한 내용은 Topological Sorting 문서를 참조하여 주십시오.
Strongly Connected Components
어떤 방향 그래프(directed graph) 가 strongly connected하다는 것은 모든 정점 쌍 (u, v)에 대해, u → v 경로와 v → u 경로가 모두 존재한다는 뜻이다. 이때 어떤 그래프의 SCC(Strongly Connected Component)란 그래프에 존재하는 strongly connected된 각 그룹들을 의미한다. 이때 SCC는 더 이상 합칠 수 없는 최대 단위로, Maximal subset이라고 볼 수 있다. 이에 따라 그래프의 모든 정점은 정확히 하나의 SCC에만 속하며, SCC들은 그래프의 정점을 서로 겹치지 않게 분할(partition) 한다.

가장 널리 쓰이는 SCC를 찾는 알고리즘은 DFS 기반의 Kosaraju’s Algorithm이다. 이는 figure 5에 그 양상이 나타나 있다. Kosaraju’s Algorithm은 아래와 같은 과정을 통해서 SCC를 찾는다.:
- 1차 DFS on G: G에 대해 DFS를 수행하고, 각 정점의 완료 순서를 스택에 저장.
- Transpose Graph Gt 생성: 모든 간선의 방향을 뒤집는다.
- 2차 DFS on Gt: 스택의 “가장 나중에 완료된 정점”[3]부터 DFS 시작.
마지막 단계를 거친 후, 각 DFS 탐색이 하나의 SCC가 된다. 따라서 해당 알고리즘의 시간 복잡도는 O(V + E)(정점 + 간선 수에 선형 비례)이므로 매우 효율적이다.