Regular Languages: 두 판 사이의 차이

2025년 10월 30일 (목) 05:08 기준 최신판

개요

해당 문서에서는 유한 오토마타(FA)를 통해 검증 가능한 언어를 의미하는 정규 언어에 대해 다룬다.

Definition of Regular Languages

어떤 언어 R이 정규 언어(regular language) 라고 불리려면, 어떤 유한 오토마타(FA) M이 R을 인식해야 한다. 이는 아래와 같다:

 $\exists M . M = F A \land M r e c o g n i z e s R$

이때 이를 증명하기 위해서는 아래와 같은 절차를 걸친다:

특정한 FA $M = (Q, Σ, δ, q_{0}, F)$ 를 정의한다.
M이 FA임을 보인다.(이는 M이 FA의 정의에 맞게 잘 구성되었는지를 확인하는 방식이다.)
M이 언어 R을 인식(recognize)하는 것을 보인다. 즉,
- a) 모든 문자열 $w \in Σ^{*}$ 에 대해, $w \in R \Rightarrow M$ 이 $w$ 를 수용(accept)
- b) 모든 문자열 $w \in Σ^{*}$ 에 대해, M이 $w$ 를 수용 $\Rightarrow w \in R$
- (a), (b)를 모두 만족해야 정확히 $L (M) = R$ ^[1]임을 보일 수 있다.

Figure 1, 2는 각각 3(a), 3(b)를 증명하는 과정이다. 먼저, figure 1은 아래와 같은 과정을 설명하는 fitch-stlye 증명이다:

목표) $\forall w \in Σ^{*} . (w \in R \Rightarrow M a c c e p t s w)$
w∈Σ*이고, w∈R이라고 가정.
- 상태열 $r_{0}, r_{1}, \dots, r_{n}$ 을 정의:
  $r_{0} = q_{0}$
  $r_{i + 1} = δ (r_{i}, w_{i + 1}), i = 0, 1, \dots, n - 1$
- 귀납법을 이용해 $r_{n} \in F$ 임을 입증
Figure 2. Proof of 3(b)
따라서 M이 $w$ 를 수용한다.

Figure 2는 아래와 같은 과정을 설명하는 fitch-stlye 증명이다:

목표) $\forall w \in Σ^{*} . (M a c c e p t s w \Rightarrow w \in R)$
w∈Σ*와, Macceptsw를 가정.
- 상태열 $r_{0}, r_{1}, \dots, r_{n}$ 을 얻는(obtain)다. 이때 상태열 $r$ 는 아래와 같다:
  $r_{0} = q_{0}$
  $r_{i + 1} = δ (r_{i}, w_{i + 1}), i = 0, 1, \dots, n - 1$
- 이로부터 $r_{n} \in F$ 임을 입증
(귀납법을 통해) $r_{n} \Rightarrow F$ 일 때, 곧 $w \in R$ 임을 보인다.

귀납법을 이용해 $r_{n} \in F$ 임을 입증

Example Problem

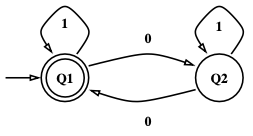
위에 대해 이해하기 위해, figure 3를 참고하여 아래와 같은 문제를 풀어보자:

Consider the example FA,
 $M = ({Q_{1}, Q_{2}}, {0, 1}, δ, Q_{1}, {Q_{1}}),$ 
where  $δ$  is given by the transition diagram figure 3.
Let  $L = {w \in {0, 1}^{*} . w h a s a n e v e n n u m b e r o f 0^{'} s}$ 
Show: The language recognized by  $M$  is  $L$ .

이를 해결하기 위한 핵심적인 아이디어는 모든 정수 $n \geq 0$ 에 대해 아래와 같은 명제 P(n)을 만드들고 증명하는 것이다:

P(n): For all  $w = w_{1} w_{2} \dots w_{n}$ 과  $r = r_{1} r_{2} \dots r_{n}$ 에 대해: 
*  $r_{0} = Q_{1}$ 
*  $r_{i + 1} = δ {r_{i}, w_{i + 1}}$ 
을 만족할 때,  $r_{n} \in {Q_{1}} \leftrightarrow w$ 에 포함된 0의 개수가 짝수

즉, “길이 n짜리 문자열을 처리했을 때, Q1에 도달하는 것 ↔ 0의 개수가 짝수”이라는 명제를 모든 n에 대해 성립함을 보이면 된다. 먼저, base case를 먼저 보자:

n = 0이면 입력이 빈 문자열이므로, 상태열은 $r_{0} = Q_{1}$ 이다.
이때 0의 개수는 0개이므로, 짝수개이다. 따라서 P(0)는 성립한다.

이제 귀납단계는 아래와 같다.

P(n)이 임의의 자연수 n에 대해 성립한다고 가정하자.
- 길이 n+1인 문자열 $w_{1} w_{2} \dots w_{n} w_{n + 1}$ 에 대해 P(n+1)이 성립함을 보여야 한다.
- 경우를 나누어 분석
  - $r_{n} \in Q_{1}, w_{n + 1} = 0 \to r_{n + 1} = Q_{2} .$ 따라서 0의 개수가 홀수
  - $r_{n} \in Q_{1}, w_{n + 1} = 1 \to r_{n + 1} = Q_{1} .$ 따라서 0의 개수가 짝수
  - $r_{n} \in Q_{2}, w_{n + 1} = 0 \to r_{n + 1} = Q_{1} .$ 따라서 0의 개수가 짝수
  - $r_{n} \in Q_{2}, w_{n + 1} = 1 \to r_{n + 1} = Q_{2} .$ 따라서 0의 개수가 홀수
- 따라서 모든 경우에서 $r_{n + 1} \in Q_{1}$ 이면 0의 개수가 짝수이다.

The Regular Operations

정규 연산(The Regular Operations)은 정규 언어를 다루는 기본적인 세가지 연산이다. 이는 아래와 같다:

Union: A∪B={x|x∈A∨x∈B}
- 즉, 언어 A 또는 언어 B 중 하나에 속하는 모든 문자열을 의미한다.
Concatenation: A∘B={xy|x∈A∧y∈B}
- 즉, A의 원소와 B의 원소를 이어붙인 문자열만을 포함하는 집합이다.
- 더욱 엄밀히 기술하면, $A \circ B = {w | \exists x, y . w = x y \land x \in A \land y \in B}$
Kleene Star: A*={x1x2⋯xk|k≥0,xi∈A}
- 즉, A의 원소들을 0번 이상 반복해서 이어붙인 문자열들의 집합을 의미한다.
- 더욱 엄밀히 기술하면 $A * = ⋃_{i \geq 0} A^{i}$ 이며, 이는 $A^{0}, A^{1}, A^{2}, . . .$ 전부 합친 집합이다. 이때,
  $A^{0} = {ϵ}$
  $A^{i + 1} = A^{i} \circ A$ (귀납적으로 정의됨 → i번 이어붙인 것에 추가로 A를 붙인 것)
- 따라서 $A *$ 는 "A를 반복적으로(concatenation) 이어붙인 결과"라고 할 수 있다.

Theorem for Kleene Star

Kleene Star에 대한 중요한 정리가 존재한다:

 $A * \circ A \subseteq A *$

즉, $A *$ 의 원소 하나와 A의 원소 하나를 이어붙여도 여전히 $A *$ 안에 포함된다. NFA를 이용한 증명은 해당 문서를 참조하십시오.

Theorem for Union

정규 언어의 합집합(union)에 대한 폐쇄성(closure)에 대한 정리가 존재한다.

 $\forall A_{1}, A_{2} . (A_{1} r e g u l a r \land A_{2} r e g u l a r) \Rightarrow (A_{1} \cup A_{2} r e g u l a r)$

즉, 두 정규 언어 $A_{1} A_{2}$ 가 있으면 $A_{1} \cup A_{2}$ 도 정규 언어라는 의미이다. 이때 중요한 것은 앞에서 다룬 $A *$ 에 대한 정리는 "한 언어 안에서"의 성질이지만, 위의 정리는 “정규 언어 전체(class)”라는 집합에 대한 성질이다. 이 정리는 알파벳이 고정되어 있지 않아도 항상 성립한다. 즉, 정규 언어들은 서로 합집합을 취해도 여전히 정규 언어라는 사실을 보장한다.

이를 증명하는 것은 아래와 같은 과정을 필요로 한다:

$A_{1}, A_{2}$ 를 임의의 정규 언어라 하자.
$A_{1}, A_{2}$ 가 정규 언어이므로, 이를 인식하는 유한 오토마타(FA) $M_{1}, M_{2}$ 가 존재한다.
이 두 오토마타를 기반으로 새로운 오토마타 $M$ 을 정의한다.
M이 정확히 $A_{1} \cup A_{2}$ 를 인식한다는 것을 보인다. 증명 완료!

따라서, 우리가 해야하는 것은 두 오토마타를 합쳐서 새로운 오토마타 $M$ 을 설계하는 방법이다. 이를 위한 아이디어는, $M_{1}, M_{2}$ 를 병렬로 동시에 돌리는 것이다. 이는 입력 문자열을 같은 속도로 읽으면서, 두 오토마타를 동시에 시뮬레이션하는 것이며, 둘 중 하나라도 accept 상태에 도달하면 최종적으로 accept하는 오토마타이다. 이는 형식적으로 아래와 같이 설계된다:

$M_{1} = (Σ, Q_{1}, δ_{1}, q_{1}, F_{1})$
$M_{2} = (Σ, Q_{2}, δ_{2}, q_{2}, F_{2})$
$M_{1} = (Σ, Q_{1} \times Q_{2}, δ, (q_{1}, q_{2}), F)$

즉, $M$ 의 상태는 " $M_{1}$ 의 상태와 $M_{2}$ 의 쌍"으로 구성된다. 이를 위한 전이 함수와 Accept 조건은 아래와 같이 설정된다:

 $δ ((r_{1}, r_{2}), a) = (δ_{1} (r_{1}, a), δ_{2} (r_{2}, a))$ ^[2]
 $F = {(r_{1}, r_{2}) | r_{1} \in F_{1} \lor r_{2} \in F_{2}}$ ^[3]

하지만 단순히 $M$ 을 정의하는 것 만으로는 부족하며, 실제로 $M r e c o g n i z e s A_{1} \cup A_{2}$ 를 증명해야 한다. 따라서 아래의 명제를 증명해야 한다.

 $\forall w \in Σ * . (M a c c e p t s w \leftrightarrow w \in A_{1} \cup A_{2})$

Only if 방향의 증명
1. 가정: $M a c c e p t s w$
2. (1)에서 $w$ 를 처리한 후의 최종 상태는 $(r_{n, 1}, r_{n, 2})$ ^[4]
3. 이는 rn,1∈F1이거나 rn,2∈F2라는 뜻이다. 따라서:
  - $r_{n, 1} \in F_{1}$ 이면, $M_{1} a c c e p t s w \to w \in A_{1}$
  - $r_{n, 2} \in F_{2}$ 이면, $M_{2} a c c e p t s w \to w \in A_{2}$
4. 결론: $w \in A_{1} \cup A_{2}$
If 방향의 증명
1. 가정: w∈A1∪A2
  - Case 1: w∈A1
    1. $M_{1} a c c e p t s w$
    2. $M$ 의 첫 성분 $r_{n, 1} \in F_{1}$
    3. 따라서 $(r_{n, 1}, r_{n, 2}) \in F$ , 즉 $M a c c e p t s w$
  - Case 2: w∈A2
    1. 대칭적인 논리로 $M_{2} a c c e p t s w$
    2. 그러면 $r_{n, 2} \in F_{2}$ , 따라서 $M a c c e p t s w$

최종적으로, $M$ 이 정의되었고, $M r e c o g n i z e s A_{1} \cup A_{2}$ 를 보였다. 따라서 $A_{1} \cup A_{2}$ 도 정규 언어이다. 즉, 정규 언어들은 합집합 연산에 대해 닫혀있음이 증명된다.

NFA를 이용한 증명은 해당 문서를 참조하십시오.

Theorem for Concatenation

정규 언어의 집합은 Concatenation(연접) 연산에 대해 닫혀 있다. 이는 아래와 같이 표현된다:

 $\forall A_{1}, A_{2} . (A_{1} r e g u l a r \land A_{2} r e g u l a r) \Rightarrow (A_{1} \circ A_{2} r e g u l a r)$

이는 두 정규 언어 $A_{1}, A_{2}$ 가 있으면 $A_{1}$ 에 속하는 문자열과 $A_{2}$ 에 속하는 문자열을 붙여 만든 새로운 언어 $A_{1} \circ A_{2}$ 역시 정규 언어이다.

이를 증명할 때, 정규언어의 합집합에 대한 정리의 증명과 같이 증명할 수 있을까? 이를 위해, concatenation의 정의가 $A \circ B = {x y | x \in \land y \in B}$ 이므로, 우리가 만들어야 하는 것은 $M_{1}, M_{2}$ 를 이용해서 $A_{1} \circ A_{2}$ 를 인식하는 새로운 오토마톤 $M$ 을 만드는 것이다. 이를 위한 직관적인 아이디어는 먼저 $M_{1}$ 을 돌려서 문자열의 앞부분 $x_{1}$ 을 읽고, 그 뒤에 $M_{2}$ 을 돌려서 문자열의 앞부분 $x_{2}$ 를 처리하는 것이다. 하지만 이를 적용할때 $x_{1}$ 과 $x_{2}$ 의 경계를 나누는 기준이 불명확하다는 문제가 있다. 따라서 Deterministic하게는 이 경계 인식을 구현하기가 어렵다.

이를 해결하기 위해서는 두 가지 방식이 있다.

모든 가능한 분할 지점을 동시에 고려
- 즉, 입력 문자열의 모든 위치를 "여기서 $x_{1}$ 이 끝나고 $x_{2}$ 가 시작할 수 있다"고 가정하고 병렬적으로 시도한다.
- 하지만 이는 DFA(Deterministic Finite Automata) 수준에서 명시적으로 구현하기는 매우 복잡하다.
Lucky Guess (행운의 추측): 우리가 마치 "여기서 x1이 끝났어" 라고 딱 맞게 추측을 하고, 그 지점부터 M2를 실행하는 방식이다. 추측이 맞으면 정규 언어에 속하고, 틀리면 속하지 않는다.
- 이는 NFA(Nondeterministic Finite Automata)의 핵심적인 아이디어이며, 이를 이용하는 것이 더욱 간단하다.

NFA를 이용한 증명은 해당 문서를 참조하십시오.

각주

↑ $L (M)$ 은 M이 인식하는 문자열의 집합을 의미한다.
↑ 이는 입력 a를 읽을 때, 각각의 오토마타가 이동한 결과를 쌍으로 저장하는 함수이다.
↑ 이는 둘 중 하나라도 accept 상태이면 M이 accept한다는 의미이다.
↑ $r_{n, 1}$ 는 n번째 문자까지 읽었을 때, 오토마톤 $M_{1}$ 의 상태를 의미한다.

[1] $L (M)$ 은 M이 인식하는 문자열의 집합을 의미한다.

[2] 이는 입력 a를 읽을 때, 각각의 오토마타가 이동한 결과를 쌍으로 저장하는 함수이다.

[3] 이는 둘 중 하나라도 accept 상태이면 M이 accept한다는 의미이다.

[4] $r_{n, 1}$ 는 n번째 문자까지 읽었을 때, 오토마톤 $M_{1}$ 의 상태를 의미한다.

[1]

[2]

[3]

[4]

@@ 133번째 줄: / 133번째 줄: @@
 자세한 내용은 [[Regular Expressions]] 문서를 참조하십시오.
-==Non-Regular Languages==
+==[[Pumping Lemma]]==
-==The Pumping Lemma==
+[[Pumping Lemma]]에 대한 자세한 설명은 해당 문서를 참조하십시오.
-DFA는 유한한 개수의 상태(state)만을 가진다. 만약 DFA가 무한한 문자열을 인식하는 언어 L 을 인식한다고 할때, 충분히 긴 문자열을 입력하면, 반드시 같은 상태를 두 번 이상 방문하게 된다. 이때 반복된 부분을 여러 번 반복(pumping)할 수 있고 여전히 DFA가 받아들이므로, DFA가 인식하는 모든 정규언어에는 특정한 반복 구조가 존재한다. 이 논리에서 pumping lemma가 출발하며, 이는 아래와 같다:
- L이 정규언어라면, 어떤 펌핑 길이 p가 존재한다.
- 이때 길이가 p 이상인 모든 문자열은 세 부분 x, y, z로 분해할 수 있으며, 아래 조건을 만족한다.
-. <math>\forall i \ge 0. xy^iz \in L</math>
-. <math>|y| > 0 </math>
-. <math>|xy| \le p</math>
-이를 논리식으로 나타내면 아래와 같다:
- <math>\forall L\,\,regular \rightarrow</math>
- <math>\qquad\exist p. \forall w. w\in L \land |w| \ge p \rightarrow</math>
- <math>\qquad\qquad\exist x\,\,y\,\,z. w =xyz \land (1) \land (2) \land (3)</math>
-먼저, 1번 조건은 y 부분을 0번, 1번, 2번… 아무 번이든 반복해도 여전히 언어 L에 속해야 한다는 것을 의미한다. 예를 들어 <math>i=0</math>일때 <math>xz</math>, <math>i=1</math>일때 <math>xyz</math>, <math>i=2</math>일때 <math>xyyz</math> 등등이 모두 L에 속해야 한다는 것이다.<br>
-또한 2번 조건은 반복 부분 y의 길이는 0이 아니며, 반드시 실제로 반복되는 구간이 존재해야 한다는 뜻이다.<br>
-마지막으로 3번째 조건은 반복되는 부분 y는 문자열의 처음 부분 p 이내에 존재해야 한다는 것이다. 즉, 반복(pumping)되는 부분은 문자열의 앞부분에 있다. 이는 DFA가 구조적으로 상태가 p개만 존재하기 때문에, 길이가 p 이상이면 반드시 어떤 상태가 다시 반복되기 때문이다.
-Pumping Lemma를 다른 말로 표현하면, <math>L\subseteq\{1\}*</math>이 정규 언어라면 <math>L</math>의 문자열 길이들의 집합은 등차수열을 포함한다는 것이다.
+==[[Grammars]]==
+자세한 내용은 [[Grammars]] 문서를 참조해주십시오.
-===Applying the Pumping Lemma===
-이는 어떤 언어가 정규언어는 아니라는 것을 보이는 데에 사용된다. 예를 들어, 아래와 같은 언어를 고려하자:
- <math>B = \{0^n1^n|n\ge 0\}</math>
-B가 정규 언어라고 가정하면, 아래와 같이 B가 정규 언어가 아님을 보일 수 있다:
-# Pumping Lemma에 따라 어떤 길이 p가 존재한다.
-# <math>w = 0^p1^p</math>로 선택한다.(길이가 <math>\ge p</math>)
-# 이때 B는 정규언어이므로, 조건에 따라 <math>w = xyz</math>로 분해된다.
-# 이때 <math>|xy| \le p</math>이므로, y는 반드시 0으로만 구성된다. <math>0 < k \le p.\,\,y = 0^k</math>
-# 이때 <math>x = 0^{p-k}, z=1^p</math>이므로, pumping lemma에 따라 이때 <math>xy^0z = 0^{p-k}1^p</math>도 B에 속해야 한다.
-# 하지만 0과 1의 개수가 다르므로 <math>xy^0z = 0^{p-k}1^p</math>는 B에 속하지 않고, 모순이 발생한다.
-위와 같은 증명의 결론은 B가 정규언어가 아니라는 것이다.
-===Using Other Facts with the PL===
-Pumping Lemma를 직접 적용하기 전에, 정규언어에 대한 다른 성질(closure property) 을 함께 이용하면 증명이 쉬워진다. 아래와 같은 언어가 비정규 언어라는 것을 증명해보자:
- <math>L=\{w\in \{0,1,2\}*|\#0(w)+\#(1)=\#(2)\}</math>
-위 언어는 자열 안의 0과 1의 개수의 합이 2의 개수와 같아야 하는 언어이다. 위 언어가 비정규임을 보이기 위해, L이 정규라고 가정하자. 또한 정규언어는 교집합에 대해 닫혀 있음(closure under intersection)을 이용하면, 아래와 같은 언어 또한 정규 언어이다:
- <math>L \cap 0*1*2* = \{0^m1^n2^{m+n}|m\ge0,n\ge0\}</math>
-이때 pumping lemma를 위 교집합 언어에 적용해보자:
-* 펌핑 길이를 p라고 하고, <math>w = 0^p0^p2^p</math>를 선택한다.
-* PL에 따라 <math>|xy|\le p</math>이므로 <math>y</math>는 오직 0으로만 이루어 져야 한다.(<math>y=0^k</math>)
-* 따라서 <math>xy^0z = 0^{p-k}1^p2^{2p}</math>가 되어야 하는데, 이는 <math>L \cap 0*1*2*</math>에 속하지 않는다.
 ==각주==

익명 사용자

검색

Regular Languages: 두 판 사이의 차이

이름공간

더 보기

문서 행위

2025년 10월 30일 (목) 05:08 기준 최신판

목차

개요

Definition of Regular Languages

Example Problem

The Regular Operations

Theorem for Kleene Star

Theorem for Union

Theorem for Concatenation

Regular Expressions

Pumping Lemma

Grammars

각주

둘러보기

둘러보기

위키 도구

위키 도구

익명 사용자

검색

Regular Languages: 두 판 사이의 차이

2025년 10월 30일 (목) 05:08 기준 최신판

개요

Definition of Regular Languages

Example Problem

The Regular Operations

Theorem for Kleene Star

Theorem for Union

Theorem for Concatenation

Regular Expressions

Pumping Lemma

Grammars

각주

둘러보기

위키 도구

문서 도구

분류 목록