Minimum Spanning Trees

상위 문서: Graph

개요

Spanning Tree는 주어진 그래프 G의 모든 정점을 포함하면서 사이클이 없는 부분 그래프이다. 그 중에서도 MST(Minimum Spanning Tree)는 G의 모든 spanning tree 중 간선 가중치의 총합이 최소인 트리를 의미한다. 이때 동일한 가중치를 가진 간선이 여러 개 있을 경우, 서로 다른 MST들이 존재할 수 있다. 또한 이는 Greedy Algorithm으로 항상 최적의 해를 얻을 수 있는 대표적인 문제이다. 하지만, 이를 해결하기 위해서는 효율적인 자료구조(우선순위 큐, Disjoint Set Union)가 필요하다.

아래는 해당 문서에서 MST에 대한 코드를 작성할 때 주어지는 그래프를 저장하는 자료구조이다:

int y;          // 간선이 연결된 정점
int weight;     // 간선의 가중치
struct edgenode *next;  // 다음 간선을 가리키는 포인터

위는 인접 리스트(adjacency list)에서 각 간선이 가중치(weight) 정보를 가지도록 확장한 형태이다.

edgenode *edges[MAXV+1]; // 각 정점의 인접 리스트 시작점
int degree[MAXV+1];      // 각 정점의 차수 (outdegree)
int nvertices;           // 정점 개수
int nedges;              // 간선 개수
int directed;            // 방향 그래프 여부

위는 그래프 구조 전체를 정의한 코드이다.

Applications of MSTs

MST 알고리즘은 여러 도시나 서버를 가장 적은 비용으로 연결하는 네크워크 구축을 하는데 사용된다. 또한 MST를 사용하여 점들을 연결한 뒤 가중치가 큰 간선을 끊어 그룹을 형성하는데 사용되기도 한다. 그 외에도, 친구 관계 그래프에서 자연스러운 친구 집단을 찾는 것과 같은 소셜 그래프 분석에도 사용된다.

MSTs and Net Partitioning

MST 알고리즘은 그래프를 여러 작은 부분으로 분할(partition)하는데 사용되기도 한다. 이는 아래와 같은 과정을 거친다:

1. 먼저 전체 그래프에서 MST를 만든다.
   • MST는 전체 정점을 모두 연결하면서도 가장 적은 비용으로 연결된 그래프이다.
   • 이를 통해 그래프 내의 "가벼운 간선"은 유지되고, "비싼 간선"은 최소화할 수 있다.
2. MST를 만든 뒤, 그 안에서 가장 큰 가중치의 간선을 하나 혹은 여러 개 제거한다.
   • 이렇게 하면 자연스럽게 그래프가 서로 잘 연결된 여러 작은 덩어리(subgraphs)로 나뉜다.

MSTs and TSP

TSP(Traveling Salesman Problem)는 외판원 문제라고도 불리며, 모든 정점(도시)을 한 번씩 방문하고 다시 출발점으로 돌아오는 최소 비용의 경로를 찾는 문제이다. 이때 MST는 TSP의 좋은 heuristic(근사 알고리즘)을 제공한다. MST를 두 번 따라가면 모든 노드를 방문하게 되고, 그 비용은 최적 TSP 경로의 2배 이내이기 때문이다. 즉, MST는 TSP의 하한(lower bound)을 제공하고, 실제 문제 해결의 출발점으로 자주 사용된다.

Prim’s Algorithm

Figure 1. Prim’s Algorithm in Action

Prim 알고리즘은 탐욕적(Greedy) 접근법을 사용해 MST를 만드는 대표적인 방법이다. 이는 아래와 같은 방법을 따른다:

1. 시작점 하나를 정하고, 그 정점에서부터 시작해 하나씩 간선을 추가하면서 트리를 확장한다.
2. 한 정점에서 출발해 주변 정점 중에서 가장 싼 간선(cheapest edge)을 선택하고, 그 정점을 트리에 추가한다.
3. 이 과정을 반복해서 결국 모든 정점이 연결될 때까지 계속 확장한다.

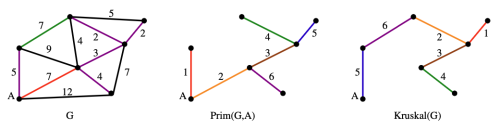
이 과정은 figure 1에 잘 설명되어 있다. 왼쪽 그림은 원래 그래프 G를 의미한다. 가운데 그림은 정점 A에서 시작해서 MST를 점차 확장한 것이다. 오른쪽 그림은 MST를 형성하는 다른 알고리즘인 kruskal 알고리즘을 G에 적용한 결과이다.

Pseudocode of Prim's Algorithm

아래는 Prim 알고리즘에 대한 수도 코드이다:

Prim-MST(G)
    임의의 시작 정점 s 선택
    While (트리에 포함되지 않은 정점이 남아있는 동안)
        Pick min cost edge between tree/non-tree vertices 
        Add the selected edge and vertex to the tree Tprim.

위 수도 코드에서 각 정점 v는 다음 세 가지 중 하나의 상태에 있다:

• In tree: 이미 MST에 포함됨
• Fringe: 트리와 연결될 수 있는 후보 정점
• Unseen: 트리와 전혀 연결되어 있지 않은 정점

Time Complexity of Prim's Algorithm

Prim 알고리즘은 자료구조에 따라 속도가 달라진다. 정점의 개수가 n이고 간선의 개수가 m인 그래프 G에 대해 가장 단순하게 구현을 한다면, 각 단계마다 트리와 트리 밖 정점 간의 최소 가중치 간선을 찾으므로, 각 단계는 O(n)의 시간 복잡도가 소요된다. 따라서 해당 과정을 모든 정점에 대해서 수행하므로 총 O(n²)의 시간복잡도가 소요된다.

이보다 효율적으로 만들려면, 우선순위 큐(min-heap)을 활용하여 간선 탐색을 매번 처음부터 하지 않을 수 있다. 이 경우, 시간 복잡도는 O((n + m)log(n))이 된다.

Prim’s Implementation

아래는 C 코드로 Prim 알고리즘을 직접 구현한 예시이다:

int prim(graph *g, int start) {
    edgenode *p;           // 간선 리스트를 순회할 포인터
    bool intree[MAXV+1];   // 정점 i가 트리에 포함되었는지 여부
    int distance[MAXV+1];  // 정점 i까지 연결되는 최소 간선 가중치
    int parent[MAXV+1];    // MST에서의 부모 정점
    int v;                 // 현재 처리 중인 정점
    int w;                 // 인접 정점
    int dist;              // 트리를 확장하기 위한 간선 중 가장 저렴한 연결 비용
    int weight = 0;        // 최종 MST의 총 가중치

    /* Initialization */
    for (int i = 1; i <= g->nvertices; i++) {
        intree[i] = false;    // 모든 정점을 intree[i] = false로 설정(아직 트리에 포함되지 않음)
        distance[i] = MAXINT; // 모든 거리를 MAXINT로 설정(연결된 간선이 없음)
        parent[i] = -1;       // 부모 없음
    }
    distance[start] = 0;      // 시작 정점(start)의 거리는 0으로 설정
    v = start;                // 현재 정점 v를 시작점으로 설정

    /* Main loop */
    while (!intree[v]) {
        intree[v] = true;     // 현재 정점 v를 트리에 포함
        if (v != start) {     // 시작점이 아니라면, 
            // parent[v]와 v를 연결하는 간선을 출력하고, 그 가중치를 weight에 더함.
            printf("edge (%d,%d) in tree\n", parent[v], v); 
            weight = weight + dist; 
        }

        /* Update distances for neighbors */
        p = g->edges[v]; 
        while (p != NULL) { // 현재 정점 v의 인접 리스트(edges[v])를 탐색.
            w = p->y;
            // 만약 현재 저장된 거리보다 더 작은 간선 가중치를 발견하면
            if ((distance[w] > p->weight) && (!intree[w])) {
                // 더 싼 가격으로 w를 트리에 포함할 수 있는 경로를 업데이트
                distance[w] = p->weight;
                parent[w] = v;
            }
            p = p->next;
        }

        // 아직 트리에 포함되지 않은 모든 정점 중에서 distance[i] 값이 가장 작은 정점을 v로 선택
        dist = MAXINT;
        for (i = 1; i <= g->nvertices; i++) {
            if ((!intree[i]) && (dist > distance[i])) {
                dist = distance[i];
                v = i;
            }
        }
    }

    return(weight);
}

위 알고리즘의 시간 복잡도를 분석하면:

1. 매번 가장 싼 간선을 찾기 위해 distance 배열 전체를 탐색 → O(n)
2. 각 정점을 트리에 추가할 때마다 인접 리스트를 확인 → O(n)
3. 이 과정을 n번 반복 → 총 O(n × n) = O(n²)

Kruskal’s Algorithm

Kruskal 알고리즘은 Prim 알고리즘과 마찬가지로 greedy 방식의 MST 알고리즘이다. 하지만 kruskal 알고리즘은 prim 알고리즘과는 접근 순서가 다르다. Prim 알고리즘이 정점 중심으로 동작한다면, kruskal 알고리즘은 간선 중심으로 동작하기 때문이다. Kruskal 알고리즘은 간선들을 오름차순으로 정렬 후, 가장 작은 간선부터 사이클이 생기지 않게 추가하는 방식이다. Figure 1을 다시 보면, kruskal 알고리즘이 어떻게 동작하는지 관찰할 수 있으며, 시작 정점이 따로 없다는 것을 알 수 있다.

Time Complexity of Kruskal's Algorithm

Kruskal 알고리즘에서 모든 간선을 정렬하는데에는 O(m log(m))의 시간 복잡도가 소요된다. 또한 각 간선에 대해 간선을 추가했을 때 사이클이 생기는지 검사하는데, 이를 DFS/BFS 알고리즘으로 수행하면 각 간선에 대해 O(n)의 시간 복잡도가 소요된다. 따라서 모든 간선에 대해서 사이클 여부를 검사하면 O(mn)의 시간 복잡도가 소요된다. 따라서 kruskal 알고리즘의 시간 복잡도는 O(m log(m) + mn) = O(mn)이 된다.

이때, 이를 Prim 알고리즘의 시간 복잡도인 O(n²)과 비교할 수 있다. 이 두 시간복잡도를 비교하면, 간선의 수가 많은 dense graph에서는 Prim 알고리즘이 유리하다는 결과가 도출된다. 반면 Kruskal 알고리즘은 간선을 정렬해서 하나씩 고르는 방식이라, 간선이 적을수록 더 효율적이다.

Fast Component Tests Give Fast MST

더욱 빠르게 사이클을 검사하여 kruskal 알고리즘을 더 효율적으로 만들 수 있는 방식이 있다. 이는 사이클을 매번 BFS/DFS로 검사하지 않고, “현재 어떤 정점이 어떤 연결요소(component)”에 속해 있는지만 빠르게 확인하는 방식이다. 기본적으로 kruskal 알고리즘은 MST를 만들면서 여러 connected component(트리 조각)를 합친다. 만약 새 간선이 같은 component의 두 정점을 연결한다면 사이클이 생기므로 이를 제외해야 한다. 따라서 kruskal 알고리즘을 구현하기 위해서는 두 가지 연산이 필요하다:

• same_component(v1, v2): 두 정점이 같은 컴포넌트에 속하는가?
• merge_components(C1, C2): 두 컴포넌트를 하나로 합치기 (Union 연산)

따라서 위 두 연산을 빠르게 수행하여 전체 알고리즘을 훨씬 빠르게 할 수 있다. 아래는 Union-Find(Disjoint Set Union, DSU) 기반으로 kruskal 알고리즘을 구현한 의사 코드이다:

모든 간선을 heap(priority queue)에 저장
count = 0
while (count < n-1)
    get next edge (v, w)
    if (component(v) ≠ component(w)) //다른 컴포넌트에 속하면 연결.
       add to T
       component(v) = component(w)

이때 해당 알고리즘에서 Union-Find 자료구조을 사용하면 사이클 검사를 O(log n) 이하로 줄여서 전체 시간복잡도를 O(m log(m))으로 개선 가능하다. 이때 O(m log(m))과 O(m log(n))을 비교하면, 그래프가 매우 커질수록 O(m log(n))이 조금 더 빠르다. 아래는 Union-Find 자료구조를 이용하여 same_component() 함수를 구현한 예시이다:

bool same_component(union_find *s, int s1, int s2) {
    return (find(s, s1) == find(s, s2));
}

Union-Find 자료구조에 대한 자세한 설명은 해당 문서를 참조하십시오.