Update of B+-Trees: 두 판 사이의 차이
| (같은 사용자의 중간 판 16개는 보이지 않습니다) | |||
| 4번째 줄: | 4번째 줄: | ||
B<sup>+</sup>-트리에서의 삽입과 삭제 개념을 소개하기 위해, 먼저 노드가 너무 커지거나 작아지지 않는다고 잠정적으로 가정해보자. 이 가정 하에서는 삽입과 삭제가 다음과 같이 수행된다: | B<sup>+</sup>-트리에서의 삽입과 삭제 개념을 소개하기 위해, 먼저 노드가 너무 커지거나 작아지지 않는다고 잠정적으로 가정해보자. 이 가정 하에서는 삽입과 삭제가 다음과 같이 수행된다: | ||
* 삽입: [[find() 함수]]에서 사용한 것과 동일한 기법을 이용하여, 삽입하려는 검색키 값을 포함할 leaf 노드를 찾는다. 그런 다음, 해당 leaf 노드에 (검색키 값, 레코드 포인터) 형태의 항목을 삽입하며, 검색키 값들이 정렬 순서를 유지하도록 위치를 조정한다. | * 삽입: [[Indexing#Queries on B+-Trees|find() 함수]]에서 사용한 것과 동일한 기법을 이용하여, 삽입하려는 검색키 값을 포함할 leaf 노드를 찾는다. 그런 다음, 해당 leaf 노드에 (검색키 값, 레코드 포인터) 형태의 항목을 삽입하며, 검색키 값들이 정렬 순서를 유지하도록 위치를 조정한다. | ||
* 삭제: find()와 동일한 방식으로 삭제할 항목이 포함된 리프 노드를 찾는다. 검색 키 값이 동일한 여러 항목이 있는 경우, 삭제할 레코드를 가리키는 항목을 찾을 때까지 이들을 탐색한다. 그런 다음 해당 항목을 리프 노드에서 제거한다. 삭제된 항목 오른쪽에 있는 모든 항목은 한 칸씩 왼쪽으로 이동하여 빈 공간이 없도록 한다. | * 삭제: find()와 동일한 방식으로 삭제할 항목이 포함된 리프 노드를 찾는다. 검색 키 값이 동일한 여러 항목이 있는 경우, 삭제할 레코드를 가리키는 항목을 찾을 때까지 이들을 탐색한다. 그런 다음 해당 항목을 리프 노드에서 제거한다. 삭제된 항목 오른쪽에 있는 모든 항목은 한 칸씩 왼쪽으로 이동하여 빈 공간이 없도록 한다. | ||
이제 노드 분할과 병합을 포함한 일반적인 삽입과 삭제 경우를 알아보아야 한다. | 이제 노드 분할과 병합을 포함한 일반적인 삽입과 삭제 경우를 알아보아야 한다. | ||
==Insertion== | |||
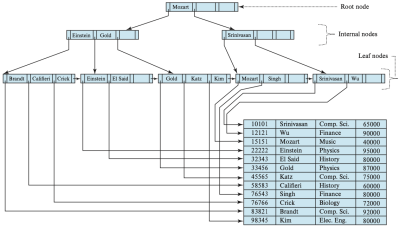
노드를 분할해야 하는 삽입 예제를 고려하기 위해, name 속성의 값이 "Adams"인 레코드를 instructor 릴레이션에 삽입한다고 하자. 그러기 위해서는 Figure 1의 B<sup>+</sup>트리에 "Adams" 항목을 삽입해야 한다. 이때 [[find() 함수]]에서의 알고리즘에서의 동일한 방식을 사용하면 Adams"는 "Brandt", "Califieri", "Crick"을 포함하는 leaf 노드에 들어가야 한다. 하지만 이 leaf 노드에는 "Adams"를 삽입할 공간이 없으므로, 해당 leaf 노드는 두개의 노드로 분할되어야 한다. Figure 2는 "Adams" 삽입으로 인해 leaf 노드가 분할된 모습을 보여준다. "Adams"와 "Brandt"는 하나의 리프에, "Califieri"와 "Crick"은 다른 리프에 위치한다. | [[파일:B+-tree for instructor file (n = 4).png|섬네일|Figure 1. B<sup>+</sup>-tree for ''instructor'' file (''n'' = 4)|400x400px]] | ||
노드를 분할해야 하는 삽입 예제를 고려하기 위해, name 속성의 값이 "Adams"인 레코드를 instructor 릴레이션에 삽입한다고 하자. 그러기 위해서는 Figure 1의 B<sup>+</sup>트리에 "Adams" 항목을 삽입해야 한다. 이때 [[Indexing#Queries on B+-Trees|find() 함수]]에서의 알고리즘에서의 동일한 방식을 사용하면 Adams"는 "Brandt", "Califieri", "Crick"을 포함하는 leaf 노드에 들어가야 한다. 하지만 이 leaf 노드에는 "Adams"를 삽입할 공간이 없으므로, 해당 leaf 노드는 두개의 노드로 분할되어야 한다. Figure 2는 "Adams" 삽입으로 인해 leaf 노드가 분할된 모습을 보여준다. "Adams"와 "Brandt"는 하나의 리프에, "Califieri"와 "Crick"은 다른 리프에 위치한다. | |||
[[파일:Split of leaf node on insertion of “Adams”.png|섬네일|Figure 2. Split of leaf node on insertion of “Adams”|400x400픽셀]] | |||
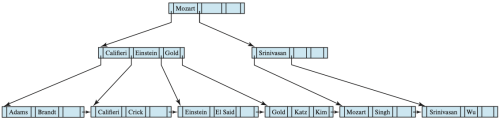
[[파일:Insertion of “Adams” into the B+-tree of Figure 1.png|섬네일|Figure 3. Insertion of “Adams” into the B+-tree of Figure 1|500x500px|가운데]] | |||
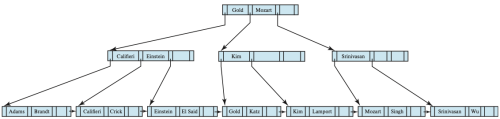
[[파일:Insertion of “Lamport” into the B+-tree of Figure 3.png|섬네일|Figure 4. Insertion of “Lamport” into the B+-tree of Figure 3|500x500px|가운데]] | |||
일반적으로는 n개의 검색키 값(리프 노드의 n−1개 키 값 + 삽입하려는 값)에서, 처음 <code>⌈n/2⌉</code> 개를 기존 노드에 유지하고 나머지를 새로 생성된 노드에 넣는다. 이때 leaf 노드를 분할한 이후에는 새 leaf 노드를 B<sup>+</sup>-트리 구조에 삽입해야 한다. 이 예제에서는 새롭게 생성된 노드의 최소 검색키 값이 "Califieri"이므로, <code>K = "Califieri"</code>이고, <code>P -> ("Califieri"로 시작하는 노드)</code>인 항목의 쌍을 부모 노드에 삽입해야 한다. Figure 3는 삽입 후의 B<sup>+</sup>트리를 보여준다. 이 경우 부모 노드에는 새 항목을 저장할 공간이 있었으므로, 추가적인 분할없이 가능했다. 만약 공간이 없었다면 부모 노드도 분할해야 하며, 이 경우, 부모의 부모에도 항목을 삽입해야 한다. 최악의 경우에는 root까지의 모든 노드가 분할되어야 할 수 있으며, root 노드가 분할되어야 할 수 있으며, 루트가 분할되면 전체 트리의 높이(height)는 1 증가한다. | |||
non-leaf 노드의 분할은 leaf 노드의 분할과는 약간 다르다. Figure 4는 figure 3에 "Lamport" 키 값을 가진 레코드를 삽입한 결과를 보여준다. "Lamport"가 삽입될 리프 노드는 이미 "Gold", "Katz", "Kim" 항목을 포함하고 있어 분할이 필요하다. 분할 결과 생성된 오른쪽 노드에는 "Kim"과 "Lamport"가 들어간다. 이 경우 <code>(Kim, n1)</code> 항목이 부모 노드에 추가되어야 하며, 여기서 n1은 새 노드를 가리키는 포인터이다. 그러나 부모 노드에 공간이 없기 때문에, 부모 노드도 분할해야 한다. 이때 부모 노드는 임시로 확장되어 항목을 추가한 후, 과도한 항목 수를 분할하여 처리한다.<br> | |||
non-leaf 노드를 분할할 때는, 자식 노드를 지시하는 포인터들을 기존의 노드와 새로 생성된 노드 사이에 나누어 배치한다. Figure 4에서는 기존의 노드가 첫 세개의 포인터를 유지하고, 새 노드는 나머지 두 개의 포인터를 가진다. 하지만 기존 노드에서의 검색키값은 이와 조금 다르게 처리된다. 새 노드로 이동된 포인터들 사이에 있는 검색 키 값들("Kim")은 해당 포인터들과 함께 이동한다. 반면, 기존 노드에 그대로 남아 있는 포인터들 사이에 있는 키 값들<code>("Califieri", "Einstein")</code>은 그대로 남는다. 이때, 기존 노드에 남는 포인터들과 새 노드로 이동하는 포인터들 사이에 위치한 검색 키 값("Gold")은 별도로 처리된다. 이는 어느 노드에도 삽입되지 않고, (Gold, n2) 항목으로 상위 부모 노드에 삽입되며, 여기서 n2는 새로 생성된 노드를 가리키는 포인터이다. 이 예제에서 부모 노드는 루트이고, 새 항목을 위한 공간이 충분했다. 아래는 B<sup>+</sup>트리에 대한 일반적인 삽입 기법이다. | |||
# 삽입이 이루어져야 할 리프 노드 l을 결정한다. | |||
# 분할이 발생하면, 새로 생성된 노드를 l의 부모에 삽입한다. | |||
# 이 삽입으로 인해 또다시 분할이 발생하면, 이를 트리 위로 재귀적으로 반복하며 처리한다. | |||
# 삽입이 더 이상 분할을 유발하지 않거나, 새로운 root 노드가 생성될 때까지 이 과정을 반복한다. | |||
===Pseudocode of the Insertion Algorithm=== | |||
아래는 위에서 다룬 알고리즘을 의사 코드로 나타낸 것이다: | |||
<syntaxhighlight lang="go"> | |||
procedure insert(value K, pointer P) | |||
if (tree is empty) create an empty leaf node L, which is also the root | |||
else Find the leaf node L that should contain key value K | |||
if (L has less than n − 1 key values) | |||
then insert_in_leaf(L, K, P) | |||
else begin /* L has n − 1 key values already, split it */ | |||
Create node L' | |||
Copy L.P₁ … L.Kₙ₋₁ to a block of memory T that can hold n (pointer, key-value) pairs | |||
insert_in_leaf(T, K, P) | |||
Set L'.Pₙ = L.Pₙ ; Set L.Pₙ = L' | |||
Erase L.P₁ through L.Kₙ₋₁ from L | |||
Copy T.P₁ through T.K[⌈n/2⌉] from T into L starting at L.P₁ | |||
Copy T.P[⌈n/2⌉+1] through T.Kₙ from T into L' starting at L'.P₁ | |||
Let K' be the smallest key-value in L' | |||
insert_in_parent(L, K', L') | |||
end | |||
</syntaxhighlight> | |||
위 의사 코드에서 L, N, P, T는 노드를 가리키는 포인터이며, L은 leaf 노드를 나타낸다. L.Ki와 L.Pi는 각각 노드 L의 i번째 키 값과 포인터를 의미하며, T.Ki 및 T.Pi도 마찬가지이다. 의사코드는 또한 노드 N의 부모를 찾기 위한 함수 <code>parent(N)</code>을 사용한다.<ref>리프 노드를 찾을 때 root에서 leaf까지의 경로에 있는 노드들의 목록을 미리 계산하면, 이후에 부모 노드를 효율적으로 찾는 데 사용할 수 있다.</ref><br> | |||
또한 <code>insert in parent</code> 절차는 인자로 N, K', N'을 받으며, 여기서 노드 N이 N과 N'으로 분할되었고, K'는 N'에서의 최소 키 값이다. 이 절차는 노드 N의 부모를 갱신하여 분할을 기록한다. <code>insert into index</code>와 <code>insert in parent</code> 절차는 노드 분할 시 내용을 임시 메모리 영역 T에 저장하여 처리한다. 절차는 수정하여 분할된 노드에서 새 노드로 데이터를 직접 복사하도록 최적화할 수 있지만, 임시 공간 T를 사용하면 절차를 단순화할 수 있다. | |||
==Deletion== | |||
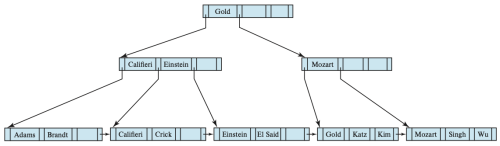
[[파일:Deletion of “Srinivasan” from the B+-tree of Figure 3.png|가운데|섬네일|500x500픽셀|Figure 5. Deletion of “Srinivasan” from the B+-tree of Figure 3]] | |||
노드 내 항목의 삭제는 해당 노드 안에 너무 적은 수의 포인터가 남는 상황을 야기할 수 있다. 우선, figure 3의 B<sup>+</sup>-트리에서 “Srinivasan”을 삭제하는 상황을 고려하자. 이 결과는 figure 5에 나타나 있다. 이를 위해서는 먼저 [[Indexing#Queries on B+-Trees|find()]] 알고리즘을 바탕으로 “Srinivasan” 항목을 찾는다. “Srinivasan” 항목을 리프 노드에서 삭제하면, 해당 노드는 “Wu” 항목 하나만 남는다. 이때 해당 figure 에서 n = 4이고, <code>1 < ⌈(n−1)/2⌉</code>이므로, 최소 절반은 차 있어야 한다는 조건을 만족시키기 위해 해당 노드를 같은 레벨에서의 노드(형제 노드)와 병합하거나 항목을 재분배 해야 한다. | |||
이 에제에서는 삭제당한 노드의 항목들을 왼쪽에 존재하는 형제 노드로 옮기고, 비어있는 오른쪽의 형제 노드를 삭제할 수 있다. 이때 노드가 삭제되면, 해당 노드를 가리키고 있던 부모 노드의 항목들도 삭제해야 한다. 예제에서 삭제할 항목은 (Srinivasan, n3)이고, n3은 “Srinivasan”이 들어 있는 leaf를 가리킨다. 해당 항목을 삭제하면, 부모 노드는 “Srinivasan”과 두 개의 포인터를 가졌던 상태에서 이제 하나의 포인터만 남게 되며, 검색키 값은 없어진다. n = 4이므로 1 < ⌈n/2⌉가 되어 부모 노드 역시 부족해진다. 이 경우 부모의 형제 노드를 살펴야 한다. Figure에서 형제 노드는 “Califieri”, “Einstein”, “Gold”를 포함하는 non-leaf 노드이다. 이때 이 노드와 병합하고 싶지만, 이 경우 포인터가 총 5개가 되어 최대값인 4를 초과하므로 병합할 수 없다. 따라서 포인터들을 재분배하여 두 노드가 최소 ⌈n/2⌉ = 2개의 자식 포인터를 갖도록 한다. | |||
재분배를 위해 왼쪽 형제 노드의 가장 오른쪽 포인터("Gold"를 가리키는 포인터)를 오른쪽에 있는 노드로 옮긴다. 이를 통해 오른쪽 형제 노드는 원래 포인터를 부족하게 가지고 있었지만, 비로소 2개의 포인터를 가짐으로서 전제 조건을 만족한다. 하지만 이 두개의 포인터는 어떤 검색키값에 의해서 구분되지 않으므로, 이 두 포인터가 가리키는 노드를 구분하기 위해서 해당 노드의 부모 노드에 있던 "Mozart"를 부족한 노드로 옮기고, "Gold" 노드를 부모 노드로 올린다. | |||
[[파일:Deletion of “Singh” and “Wu” from the B+-tree of Figure 5.png|가운데|섬네일|500x500픽셀|Figure 6. Deletion of “Singh” and “Wu” from the B+-tree of Figure 5]] | |||
다음으로, fiugre 5의 B<sup>+</sup>트리에서 검색키 값 "Singh"와 "Wu"를 삭제한다고 가정하자. 그 결과는 figure 6와 같다. 이 중 "Singh"의 삭제는 구조적으로 문제를 일으키지 않지만, "Wu"의 삭제는 leaf 노드가 조건<ref>Leaf 노드들은 ⌈(n-1)/2⌉ ~ n-1개의 검색키 값들을 가져야 한다.</ref>에 미달하도록 한다. 이때 왼쪽의 형제노드는 이미 최대 크기이므로, 값을 재분배해야 한다. 따라서 "Kim"이 속한 항목을 오른쪽의 "Mozart"가 속한 노드로 이동시켜 재분배한다. 또한, 부모 노드에서의 구분값은 "Mozart"에서 "Kim"으로 갱신된다. | |||
[[파일:Deletion of “Gold” from the B+-tree of Figure 6.png|가운데|섬네일|500x500픽셀|Figure 7. Deletion of “Gold” from the B+-tree of Figure 6]] | |||
Figure 6에서 "Gold"를 삭제하면, 그 결과는 figure 7과 같다. "Gold"의 삭제는 leaf 노드를 조건에 미달하도록 하며, 형제 노드와 병합하여 이를 해결한다. 이 과정에서 부모 노드("Kim"을 포함한 비리프 노드)에서의 항목이 삭제되며, 이에 따라 부모 노드도 미달 상태가 된다. 이 상황에서는 부모 노드가 형제 노드와 결합 가능하며, 따라서 부모 노드가 서로 병합되면서 부모의 부모 노드(root 노드)에 있던 "Gold"가 병합된 노드로 내려온다. 이에 따라 root 노드 또한 조건에 미달하게 되어 삭제되고, 부모 노드가 root 노드가 되며 B<sup>+</sup>-트리의 높이가 1 감소한다. | |||
이때 주의할 점은 삭제 결과로 인해 leaf 노드에는 더 이상 존재하지 않는 검색키값이 non-leaf 노드에는 존재할 수 있다는 것이다. 예를 들어 figure 7에서 "Gold"는 leaf 노드에서 삭제되었으나, non-leaf 노드에는 계속 존재한다. 아래는 B<sup>+</sup>트리에 대한 일반적인 삽입 기법이다: | |||
* leaf 노드에서 목표한 값을 삭제한다. | |||
* 해당 leaf 노드가 너무 작아져서 삭제해야 한다면, 부모 노드에서도 해당 항목을 삭제한다. | |||
* 이 과정은 root 노드까지 재귀적으로 적용되거나, 부모 노드가 삭제 후에도 충분히 크거나, 삭제가 아닌 재분배가 일어날 때까지 반복한다. | |||
===Pseudocode of the Deletion Algorithm=== | |||
아래는 은 B<sup>+</sup>-트리에서 삭제를 수행하는 의사코드이다: | |||
<syntaxhighlight lang="go"> | |||
procedure delete(value K, pointer P) | |||
find the leaf node L that contains (K, P) | |||
delete_entry(L, K, P) | |||
procedure delete_entry(node N, value K, pointer P) | |||
delete (K, P) from N | |||
if (N is the root and N has only one remaining child) | |||
then make the child of N the new root of the tree and delete N | |||
else if (N has too few values/pointers) then begin | |||
Let N' be the previous or next child of parent(N) | |||
Let K' be the value between pointers N and N' in parent(N) | |||
if (entries in N and N' can fit in a single node) | |||
then begin /* Coalesce nodes */ | |||
if (N is a predecessor of N') then swap_variables(N, N') | |||
if (N is not a leaf) | |||
then append K' and all pointers and values in N to N' | |||
else append all (Kᵢ, Pᵢ) pairs in N to N'; set N'.Pₙ = N.Pₙ | |||
delete_entry(parent(N), K', N); delete node N | |||
end | |||
else begin /* Redistribution: borrow an entry from N' */ | |||
if (N' is a predecessor of N) then begin | |||
if (N is a nonleaf node) then begin | |||
let m be such that N'.Pₘ is the last pointer in N' | |||
remove (N'.Kₘ₋₁, N'.Pₘ) from N' | |||
insert (N'.Pₘ, K') as the first pointer and value in N, | |||
by shifting other pointers and values right | |||
replace K' in parent(N) by N'.Kₘ₋₁ | |||
end | |||
else begin | |||
let m be such that (N'.Pₘ, N'.Kₘ) is the last pointer/value pair in N' | |||
remove (N'.Pₘ, N'.Kₘ) from N' | |||
insert (N'.Pₘ, N'.Kₘ) as the first pointer and value in N, | |||
by shifting other pointers and values right | |||
replace K' in parent(N) by N'.Kₘ | |||
end | |||
end | |||
else … symmetric to the then case … | |||
end | |||
end | |||
</syntaxhighlight> | |||
위 코드에서 <code>swap variables(N, N')</code> 함수는 단순히 변수 N과 N'의 값을 바꾸는 역할을 하며, 트리 구조 자체에는 영향이 없다. | |||
==Complexity of B<sup>+</sup>-Tree Updates== | |||
B<sup>+</sup>-트리 구조의 삽입/삭제 연산이 복잡하더라도, 이는 상대적으로 적은 수의 I/O 연산을 필요로 하며, 이는 중요한 이점이다. 삽입/삭제 연산에 대해 요구되는 I/O 연산의 수는 최악의 경우 <code>log<sub>⌈n∕2⌉</sub>(N)</code>에 비례하기 때문이다. <ref>삭제 연산의 경우는, 검색키가 중복되지 않는다는 전제 조건을 필요로 한다.</ref> 이에 따라 B<sup>+</sup>-트리 구조의 삽입/삭제 연산은 속도가 빠르다. | |||
B<sup>+</sup>-트리에서 실제로 필요한 연산의 수는 더 적다. 예를 들어 fan-out<ref>트리 기반 자료구조에서 하나의 노드가 가질 수 있는 최대 자식 수이다.</ref>이 100이고, 각 leaf 노드에 대한 접근이 균등하다면, leaf 노드의 부모 노드는 leaf 노드보다 100배 더 자주 접근된다. 반대로 말하면, non-leaf 노드 부모 개수는 leaf 노드의 개수의 1/100보다 약간 더 많은 수준이다. 따라서 대부분의 non-leaf 노드는 데이터베이스 버퍼에 존재하며, 결과적으로 한번의 탐색에 1~2회의 I/O 연산만이 필요하다. 또한 대부분의 삽입/삭제 연산은 분할, 합병 등을 필요로 하지 않으며, 분할, 합병은 매우 적은 빈도로 일어난다. 이에 따라 대부분의 삽입/삭제 연산은 leaf 노드에만 영향을 준다. | |||
B<sup>+</sup>-트리는 최소한 노드가 절반은 차있도록 강제하지만, 실제 상황에서는 삽입되는 항목들의 정렬 여부에 따라 그 결과가 다르다. 항목들이 무작위 순서로 삽입된다면 트리 구조 내의 노드는 평균적으로 2/3 이상 차있다. 하지만 정렬된 순서로 삽입될 경우, 노드는 1/2 정도만 점유된다. | |||
==각주== | ==각주== | ||
2025년 6월 11일 (수) 04:57 기준 최신판
개요
레코드(Record)가 릴레이션(relation)에 삽입/삭제(insert/delete)될 때, 해당 릴레이션에 대한 인덱스들도 이에 맞게 갱신되어야 한다. 이때 레코드에 대한 갱신(upadate) 작업은 기존 레코드를 삭제한 후, 그 위치에 갱신된 레코드를 삽입하는 것으로 수행될 수 있다. 따라서 삽입/삭제 작업만을 고려하면 된다. 이때 삽입과 삭제 작업은 조회(lookup)보다 더 복잡한데, 삽입 결과로 노드가 너무 커질 경우, 분할(split)이 필요하고, 삭제 결과로 노드가 너무 적어질 경우(⌈n/2⌉ 포인터보다 적은 경우)에는 노드 사이의 결합이 필요할 수 있기 때문이다. 이때 노드를 분할하거나 병합할 때는 트리의 균형(balance)이 유지되도록 해야 한다.
B+-트리에서의 삽입과 삭제 개념을 소개하기 위해, 먼저 노드가 너무 커지거나 작아지지 않는다고 잠정적으로 가정해보자. 이 가정 하에서는 삽입과 삭제가 다음과 같이 수행된다:
- 삽입: find() 함수에서 사용한 것과 동일한 기법을 이용하여, 삽입하려는 검색키 값을 포함할 leaf 노드를 찾는다. 그런 다음, 해당 leaf 노드에 (검색키 값, 레코드 포인터) 형태의 항목을 삽입하며, 검색키 값들이 정렬 순서를 유지하도록 위치를 조정한다.
- 삭제: find()와 동일한 방식으로 삭제할 항목이 포함된 리프 노드를 찾는다. 검색 키 값이 동일한 여러 항목이 있는 경우, 삭제할 레코드를 가리키는 항목을 찾을 때까지 이들을 탐색한다. 그런 다음 해당 항목을 리프 노드에서 제거한다. 삭제된 항목 오른쪽에 있는 모든 항목은 한 칸씩 왼쪽으로 이동하여 빈 공간이 없도록 한다.
이제 노드 분할과 병합을 포함한 일반적인 삽입과 삭제 경우를 알아보아야 한다.
Insertion
노드를 분할해야 하는 삽입 예제를 고려하기 위해, name 속성의 값이 "Adams"인 레코드를 instructor 릴레이션에 삽입한다고 하자. 그러기 위해서는 Figure 1의 B+트리에 "Adams" 항목을 삽입해야 한다. 이때 find() 함수에서의 알고리즘에서의 동일한 방식을 사용하면 Adams"는 "Brandt", "Califieri", "Crick"을 포함하는 leaf 노드에 들어가야 한다. 하지만 이 leaf 노드에는 "Adams"를 삽입할 공간이 없으므로, 해당 leaf 노드는 두개의 노드로 분할되어야 한다. Figure 2는 "Adams" 삽입으로 인해 leaf 노드가 분할된 모습을 보여준다. "Adams"와 "Brandt"는 하나의 리프에, "Califieri"와 "Crick"은 다른 리프에 위치한다.

일반적으로는 n개의 검색키 값(리프 노드의 n−1개 키 값 + 삽입하려는 값)에서, 처음 ⌈n/2⌉ 개를 기존 노드에 유지하고 나머지를 새로 생성된 노드에 넣는다. 이때 leaf 노드를 분할한 이후에는 새 leaf 노드를 B+-트리 구조에 삽입해야 한다. 이 예제에서는 새롭게 생성된 노드의 최소 검색키 값이 "Califieri"이므로, K = "Califieri"이고, P -> ("Califieri"로 시작하는 노드)인 항목의 쌍을 부모 노드에 삽입해야 한다. Figure 3는 삽입 후의 B+트리를 보여준다. 이 경우 부모 노드에는 새 항목을 저장할 공간이 있었으므로, 추가적인 분할없이 가능했다. 만약 공간이 없었다면 부모 노드도 분할해야 하며, 이 경우, 부모의 부모에도 항목을 삽입해야 한다. 최악의 경우에는 root까지의 모든 노드가 분할되어야 할 수 있으며, root 노드가 분할되어야 할 수 있으며, 루트가 분할되면 전체 트리의 높이(height)는 1 증가한다.
non-leaf 노드의 분할은 leaf 노드의 분할과는 약간 다르다. Figure 4는 figure 3에 "Lamport" 키 값을 가진 레코드를 삽입한 결과를 보여준다. "Lamport"가 삽입될 리프 노드는 이미 "Gold", "Katz", "Kim" 항목을 포함하고 있어 분할이 필요하다. 분할 결과 생성된 오른쪽 노드에는 "Kim"과 "Lamport"가 들어간다. 이 경우 (Kim, n1) 항목이 부모 노드에 추가되어야 하며, 여기서 n1은 새 노드를 가리키는 포인터이다. 그러나 부모 노드에 공간이 없기 때문에, 부모 노드도 분할해야 한다. 이때 부모 노드는 임시로 확장되어 항목을 추가한 후, 과도한 항목 수를 분할하여 처리한다.
non-leaf 노드를 분할할 때는, 자식 노드를 지시하는 포인터들을 기존의 노드와 새로 생성된 노드 사이에 나누어 배치한다. Figure 4에서는 기존의 노드가 첫 세개의 포인터를 유지하고, 새 노드는 나머지 두 개의 포인터를 가진다. 하지만 기존 노드에서의 검색키값은 이와 조금 다르게 처리된다. 새 노드로 이동된 포인터들 사이에 있는 검색 키 값들("Kim")은 해당 포인터들과 함께 이동한다. 반면, 기존 노드에 그대로 남아 있는 포인터들 사이에 있는 키 값들("Califieri", "Einstein")은 그대로 남는다. 이때, 기존 노드에 남는 포인터들과 새 노드로 이동하는 포인터들 사이에 위치한 검색 키 값("Gold")은 별도로 처리된다. 이는 어느 노드에도 삽입되지 않고, (Gold, n2) 항목으로 상위 부모 노드에 삽입되며, 여기서 n2는 새로 생성된 노드를 가리키는 포인터이다. 이 예제에서 부모 노드는 루트이고, 새 항목을 위한 공간이 충분했다. 아래는 B+트리에 대한 일반적인 삽입 기법이다.
- 삽입이 이루어져야 할 리프 노드 l을 결정한다.
- 분할이 발생하면, 새로 생성된 노드를 l의 부모에 삽입한다.
- 이 삽입으로 인해 또다시 분할이 발생하면, 이를 트리 위로 재귀적으로 반복하며 처리한다.
- 삽입이 더 이상 분할을 유발하지 않거나, 새로운 root 노드가 생성될 때까지 이 과정을 반복한다.
Pseudocode of the Insertion Algorithm
아래는 위에서 다룬 알고리즘을 의사 코드로 나타낸 것이다:
procedure insert(value K, pointer P)
if (tree is empty) create an empty leaf node L, which is also the root
else Find the leaf node L that should contain key value K
if (L has less than n − 1 key values)
then insert_in_leaf(L, K, P)
else begin /* L has n − 1 key values already, split it */
Create node L'
Copy L.P₁ … L.Kₙ₋₁ to a block of memory T that can hold n (pointer, key-value) pairs
insert_in_leaf(T, K, P)
Set L'.Pₙ = L.Pₙ ; Set L.Pₙ = L'
Erase L.P₁ through L.Kₙ₋₁ from L
Copy T.P₁ through T.K[⌈n/2⌉] from T into L starting at L.P₁
Copy T.P[⌈n/2⌉+1] through T.Kₙ from T into L' starting at L'.P₁
Let K' be the smallest key-value in L'
insert_in_parent(L, K', L')
end
위 의사 코드에서 L, N, P, T는 노드를 가리키는 포인터이며, L은 leaf 노드를 나타낸다. L.Ki와 L.Pi는 각각 노드 L의 i번째 키 값과 포인터를 의미하며, T.Ki 및 T.Pi도 마찬가지이다. 의사코드는 또한 노드 N의 부모를 찾기 위한 함수 parent(N)을 사용한다.[1]
또한 insert in parent 절차는 인자로 N, K', N'을 받으며, 여기서 노드 N이 N과 N'으로 분할되었고, K'는 N'에서의 최소 키 값이다. 이 절차는 노드 N의 부모를 갱신하여 분할을 기록한다. insert into index와 insert in parent 절차는 노드 분할 시 내용을 임시 메모리 영역 T에 저장하여 처리한다. 절차는 수정하여 분할된 노드에서 새 노드로 데이터를 직접 복사하도록 최적화할 수 있지만, 임시 공간 T를 사용하면 절차를 단순화할 수 있다.
Deletion
노드 내 항목의 삭제는 해당 노드 안에 너무 적은 수의 포인터가 남는 상황을 야기할 수 있다. 우선, figure 3의 B+-트리에서 “Srinivasan”을 삭제하는 상황을 고려하자. 이 결과는 figure 5에 나타나 있다. 이를 위해서는 먼저 find() 알고리즘을 바탕으로 “Srinivasan” 항목을 찾는다. “Srinivasan” 항목을 리프 노드에서 삭제하면, 해당 노드는 “Wu” 항목 하나만 남는다. 이때 해당 figure 에서 n = 4이고, 1 < ⌈(n−1)/2⌉이므로, 최소 절반은 차 있어야 한다는 조건을 만족시키기 위해 해당 노드를 같은 레벨에서의 노드(형제 노드)와 병합하거나 항목을 재분배 해야 한다.
이 에제에서는 삭제당한 노드의 항목들을 왼쪽에 존재하는 형제 노드로 옮기고, 비어있는 오른쪽의 형제 노드를 삭제할 수 있다. 이때 노드가 삭제되면, 해당 노드를 가리키고 있던 부모 노드의 항목들도 삭제해야 한다. 예제에서 삭제할 항목은 (Srinivasan, n3)이고, n3은 “Srinivasan”이 들어 있는 leaf를 가리킨다. 해당 항목을 삭제하면, 부모 노드는 “Srinivasan”과 두 개의 포인터를 가졌던 상태에서 이제 하나의 포인터만 남게 되며, 검색키 값은 없어진다. n = 4이므로 1 < ⌈n/2⌉가 되어 부모 노드 역시 부족해진다. 이 경우 부모의 형제 노드를 살펴야 한다. Figure에서 형제 노드는 “Califieri”, “Einstein”, “Gold”를 포함하는 non-leaf 노드이다. 이때 이 노드와 병합하고 싶지만, 이 경우 포인터가 총 5개가 되어 최대값인 4를 초과하므로 병합할 수 없다. 따라서 포인터들을 재분배하여 두 노드가 최소 ⌈n/2⌉ = 2개의 자식 포인터를 갖도록 한다.
재분배를 위해 왼쪽 형제 노드의 가장 오른쪽 포인터("Gold"를 가리키는 포인터)를 오른쪽에 있는 노드로 옮긴다. 이를 통해 오른쪽 형제 노드는 원래 포인터를 부족하게 가지고 있었지만, 비로소 2개의 포인터를 가짐으로서 전제 조건을 만족한다. 하지만 이 두개의 포인터는 어떤 검색키값에 의해서 구분되지 않으므로, 이 두 포인터가 가리키는 노드를 구분하기 위해서 해당 노드의 부모 노드에 있던 "Mozart"를 부족한 노드로 옮기고, "Gold" 노드를 부모 노드로 올린다.
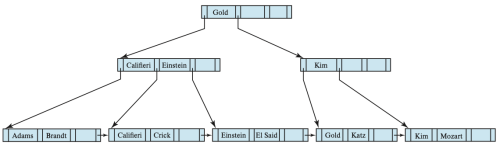
다음으로, fiugre 5의 B+트리에서 검색키 값 "Singh"와 "Wu"를 삭제한다고 가정하자. 그 결과는 figure 6와 같다. 이 중 "Singh"의 삭제는 구조적으로 문제를 일으키지 않지만, "Wu"의 삭제는 leaf 노드가 조건[2]에 미달하도록 한다. 이때 왼쪽의 형제노드는 이미 최대 크기이므로, 값을 재분배해야 한다. 따라서 "Kim"이 속한 항목을 오른쪽의 "Mozart"가 속한 노드로 이동시켜 재분배한다. 또한, 부모 노드에서의 구분값은 "Mozart"에서 "Kim"으로 갱신된다.

Figure 6에서 "Gold"를 삭제하면, 그 결과는 figure 7과 같다. "Gold"의 삭제는 leaf 노드를 조건에 미달하도록 하며, 형제 노드와 병합하여 이를 해결한다. 이 과정에서 부모 노드("Kim"을 포함한 비리프 노드)에서의 항목이 삭제되며, 이에 따라 부모 노드도 미달 상태가 된다. 이 상황에서는 부모 노드가 형제 노드와 결합 가능하며, 따라서 부모 노드가 서로 병합되면서 부모의 부모 노드(root 노드)에 있던 "Gold"가 병합된 노드로 내려온다. 이에 따라 root 노드 또한 조건에 미달하게 되어 삭제되고, 부모 노드가 root 노드가 되며 B+-트리의 높이가 1 감소한다.
이때 주의할 점은 삭제 결과로 인해 leaf 노드에는 더 이상 존재하지 않는 검색키값이 non-leaf 노드에는 존재할 수 있다는 것이다. 예를 들어 figure 7에서 "Gold"는 leaf 노드에서 삭제되었으나, non-leaf 노드에는 계속 존재한다. 아래는 B+트리에 대한 일반적인 삽입 기법이다:
- leaf 노드에서 목표한 값을 삭제한다.
- 해당 leaf 노드가 너무 작아져서 삭제해야 한다면, 부모 노드에서도 해당 항목을 삭제한다.
- 이 과정은 root 노드까지 재귀적으로 적용되거나, 부모 노드가 삭제 후에도 충분히 크거나, 삭제가 아닌 재분배가 일어날 때까지 반복한다.
Pseudocode of the Deletion Algorithm
아래는 은 B+-트리에서 삭제를 수행하는 의사코드이다:
procedure delete(value K, pointer P)
find the leaf node L that contains (K, P)
delete_entry(L, K, P)
procedure delete_entry(node N, value K, pointer P)
delete (K, P) from N
if (N is the root and N has only one remaining child)
then make the child of N the new root of the tree and delete N
else if (N has too few values/pointers) then begin
Let N' be the previous or next child of parent(N)
Let K' be the value between pointers N and N' in parent(N)
if (entries in N and N' can fit in a single node)
then begin /* Coalesce nodes */
if (N is a predecessor of N') then swap_variables(N, N')
if (N is not a leaf)
then append K' and all pointers and values in N to N'
else append all (Kᵢ, Pᵢ) pairs in N to N'; set N'.Pₙ = N.Pₙ
delete_entry(parent(N), K', N); delete node N
end
else begin /* Redistribution: borrow an entry from N' */
if (N' is a predecessor of N) then begin
if (N is a nonleaf node) then begin
let m be such that N'.Pₘ is the last pointer in N'
remove (N'.Kₘ₋₁, N'.Pₘ) from N'
insert (N'.Pₘ, K') as the first pointer and value in N,
by shifting other pointers and values right
replace K' in parent(N) by N'.Kₘ₋₁
end
else begin
let m be such that (N'.Pₘ, N'.Kₘ) is the last pointer/value pair in N'
remove (N'.Pₘ, N'.Kₘ) from N'
insert (N'.Pₘ, N'.Kₘ) as the first pointer and value in N,
by shifting other pointers and values right
replace K' in parent(N) by N'.Kₘ
end
end
else … symmetric to the then case …
end
end
위 코드에서 swap variables(N, N') 함수는 단순히 변수 N과 N'의 값을 바꾸는 역할을 하며, 트리 구조 자체에는 영향이 없다.
Complexity of B+-Tree Updates
B+-트리 구조의 삽입/삭제 연산이 복잡하더라도, 이는 상대적으로 적은 수의 I/O 연산을 필요로 하며, 이는 중요한 이점이다. 삽입/삭제 연산에 대해 요구되는 I/O 연산의 수는 최악의 경우 log⌈n∕2⌉(N)에 비례하기 때문이다. [3] 이에 따라 B+-트리 구조의 삽입/삭제 연산은 속도가 빠르다.
B+-트리에서 실제로 필요한 연산의 수는 더 적다. 예를 들어 fan-out[4]이 100이고, 각 leaf 노드에 대한 접근이 균등하다면, leaf 노드의 부모 노드는 leaf 노드보다 100배 더 자주 접근된다. 반대로 말하면, non-leaf 노드 부모 개수는 leaf 노드의 개수의 1/100보다 약간 더 많은 수준이다. 따라서 대부분의 non-leaf 노드는 데이터베이스 버퍼에 존재하며, 결과적으로 한번의 탐색에 1~2회의 I/O 연산만이 필요하다. 또한 대부분의 삽입/삭제 연산은 분할, 합병 등을 필요로 하지 않으며, 분할, 합병은 매우 적은 빈도로 일어난다. 이에 따라 대부분의 삽입/삭제 연산은 leaf 노드에만 영향을 준다.
B+-트리는 최소한 노드가 절반은 차있도록 강제하지만, 실제 상황에서는 삽입되는 항목들의 정렬 여부에 따라 그 결과가 다르다. 항목들이 무작위 순서로 삽입된다면 트리 구조 내의 노드는 평균적으로 2/3 이상 차있다. 하지만 정렬된 순서로 삽입될 경우, 노드는 1/2 정도만 점유된다.